Практическая работа № 4 (1ч)
Вычисление определенных интегралов.
Вычислить определённые интегралы:
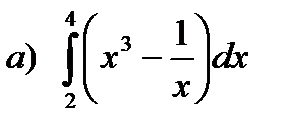 ;
; 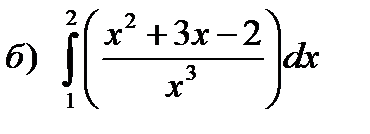 ;
;
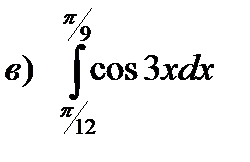 ;
; 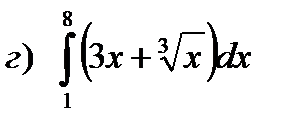 ;
;
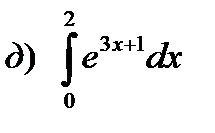 ;
; 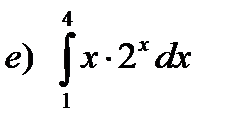 .
.
Тема 7. Дифференциальные уравнения.
Содержание программы
7.1. Понятие дифференциального уравнения 1-го порядка. Дифференциальное уравнение с разделяющимися переменными.
7.2. Однородное дифференциальное уравнение.
7.3. Понятие дифференциального уравнения высшего порядка. Дифференциальные уравнения, которые допускают понижение порядка.
Содержание темы
Дифференциальным называется такое уравнение, в котором неизвестной является функция одной или нескольких переменных, причем в уравнение входит не только сама функция, но и ее производные.
Если неизвестная функция является функцией от одной переменной, то уравнение называется обыкновенным дифференциальным, если функция нескольких переменных – то дифференциальным уравнением в частных производных.
Порядок наивысшей производной (дифференциала), входящей в дифференциальное уравнение, называется порядком уравнения.
Любая функция, удовлетворяющая дифференциальному уравнению, называется решением или интегралом этого уравнения.
Например, фукнция у = cos x есть решение дифференциального уравнения
у//+у=0.
В самом деле, для функции у = cos x имеем у// = - cos x, поэтому, подставив в уравнение значения у и у//, получим тождество.
Решение дифференциального уравнения, в котором число произвольных постоянных равно порядку дифференциального уравнения, называется общим решением данного уравнения. Решение дифференциального уравнения при определенных значениях постоянных называется частным решением.
На практике, как правило, частное решение некоторого дифференциального уравнения находится из общего решения не путем придания произвольным постоянным каких-то определенных численных значений, а исходя из некоторых условий, которым должно удовлетворять искомое частное решение. Условия, которым должно удовлетворять искомое частное решение данного дифференциального уравнения, называются начальными условиями.
Задача отыскания конкретного частного решения данного дифференциального уравнения по начальным данным называется задачей Коши.
Соотношение, связывающее независимую переменную х, неизвестную функцию у = у(х) и её первую производную у /, называется обыкновенным дифференциальным уравнением первого порядка:
F (x, y, y /) = 0.
Решением дифференциального уравнения называется функция у = у(х), удовлетворяющая этому уравнению. Общее решение дифференциального уравнения первого порядка – это множество функций, зависящих от одной произвольной постоянной С: у = φ (х, С). Частное решение дифференциального уравнения получается из общего решения при значении произвольной постоянной, определяемом начальным условием у(х0) = у0.
Задача Коши для дифференциального уравнения первого порядка ставится следующим образом: найти частное решение, удовлетворяющее начальному условию у(х0) = у0.
Дифференциальным уравнением первого порядка с разделяющимися переменными называется уравнение вида
M1(x) N1(y) dx + M2(x) N2(y) dy = 0
Схема решениядифференциального уравнения первого порядка с разделяющимися переменными:
1) Разделим переменные: M2(x) N2(y) dy = - M1(x) N1(y) dx,
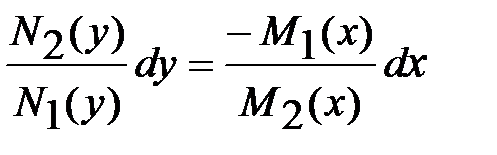 ,
,
2) Проинтегрируем обе части тождества:
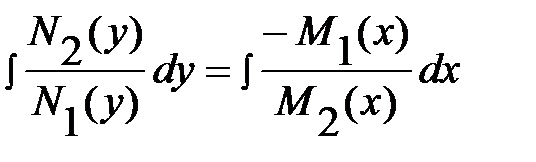 .
.
Пример 7.1. Найти общее решение дифференциального уравнения
(х2 + 1) у/ = 2ху.
Решение (х2 + 1) у/ = 2ху
(х2 + 1) 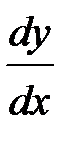 = 2ху
= 2ху
(х2 + 1) dу = 2ху dx
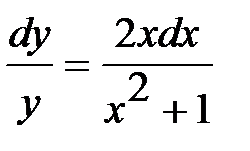
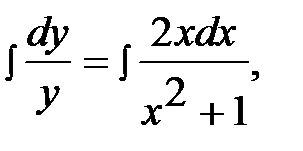
ln |y| = ln |x2 + 1| + ln |C|,
ln |y| = ln |C(x2 + 1)|,
y = C(x2 + 1) – общее решение.
Ответ: y = C(x2 + 1), где С = const.
Пример 7.2. Решить задачу Коши (х + 3) y/ = (y + 2), y(2) = 3.
Решение (х + 3) y/ = (y + 2),
(х + 3) 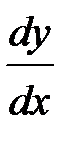 = (y + 2),
= (y + 2),
(x + 3) dy = (y + 2) dx,
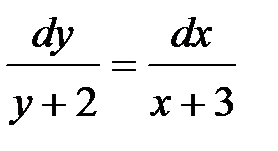 ,
,
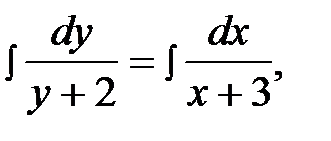
ln |y + 2| = ln |x + 3| + ln |C|,
ln |y + 2| = ln |C(x + 3)|,
y + 2= C(x + 3)
y = C (x + 3) – 2 – общее решение.
Решим задачу Коши, найдя значение С, удовлетворяющее заданным начальным условиям y(2) = 3:
С (2 + 3) – 2 = 3,
5С = 5,
С = 1.
Подставив в общее решение найденное значение С, получим частное решение дифференциального уравнения:
у = (х + 3) – 2,
у = х + 1.
Ответ: у = х + 1.
Дифференциальное уравнение вида 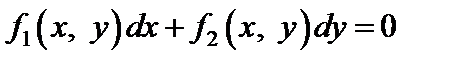 называют однородным, если обе функции
называют однородным, если обе функции 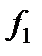 и
и 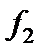 являются однородными функциями одной и той же степени n, т. е. для параметра t выполняются:
являются однородными функциями одной и той же степени n, т. е. для параметра t выполняются: 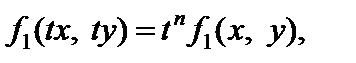
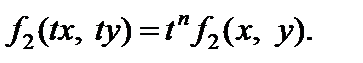
Однородное уравнение может быть сведено к виду
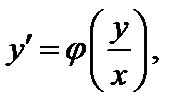 (7.1)
(7.1)
где 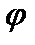 – некоторое выражение относительно
– некоторое выражение относительно 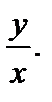
Для решения однородного уравнения его сводят вначале к виду (7.1), а затем заменяют 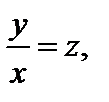 где
где 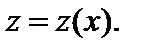 Этой заменой дифференциальное уравнение (7.1) приводится к уравнению с разделяющимися переменными. Иногда целесообразнее сделать замену
Этой заменой дифференциальное уравнение (7.1) приводится к уравнению с разделяющимися переменными. Иногда целесообразнее сделать замену 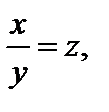 где
где 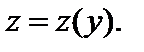
Пример 7.3. Решить уравнения:
1) 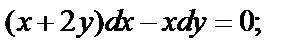 2)
2) 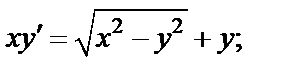
3) 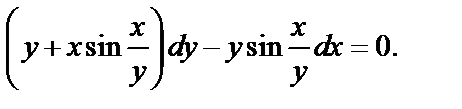
Решение 1) 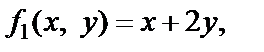
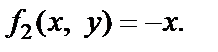 Так как
Так как
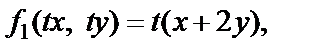
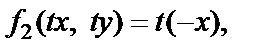
то 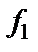 и
и 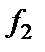 – однородные функции первой степени.
– однородные функции первой степени.
Делаем замену. Очевидно, что делением на 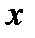
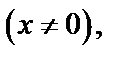 уравнение сводится к виду
уравнение сводится к виду 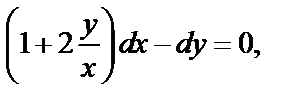 т. е.
т. е. 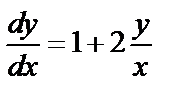 или
или 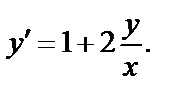 Заменяем
Заменяем 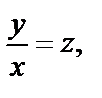 где
где 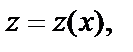 откуда
откуда 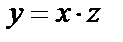 и
и 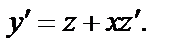 Подставляя в исходное дифференциальное уравнение, получаем:
Подставляя в исходное дифференциальное уравнение, получаем: 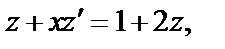 т. е.
т. е. 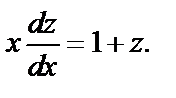
Разделяем переменные (при условии 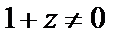 ):
): 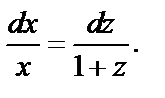 Интегрируем:
Интегрируем: 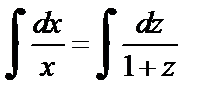 или
или 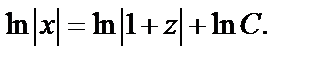 Отсюда
Отсюда 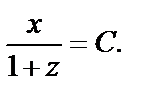
Возвращаемся к старым переменным, подставляем вместо z выражение 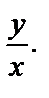 Тогда общий интеграл исходного дифференциального уравнения имеет вид:
Тогда общий интеграл исходного дифференциального уравнения имеет вид: 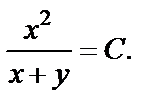
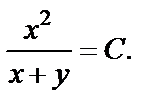
Рассмотрим отдельно возможные решения 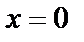 и
и 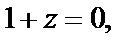 которые мы исключали. В последнем случае имеем
которые мы исключали. В последнем случае имеем 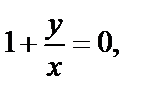 т. е.
т. е. 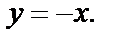 Подставляем
Подставляем 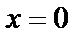 и
и 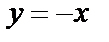 в заданное дифференциальное уравнение и убеждаемся, что они также являются его решениями. При этом решение
в заданное дифференциальное уравнение и убеждаемся, что они также являются его решениями. При этом решение 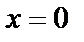 содержится в формуле общего интеграла при
содержится в формуле общего интеграла при 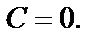 Решение
Решение 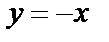 не содержится в полученной формуле общего интеграла. Поэтому окончательное решение:
не содержится в полученной формуле общего интеграла. Поэтому окончательное решение: 
2) Разделив дифференциальное уравнение на x 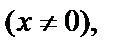 получаем:
получаем: 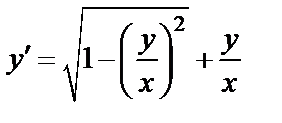 – это однородное дифференциальное уравнение. После замены
– это однородное дифференциальное уравнение. После замены 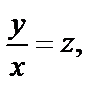 где
где 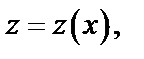 имеем
имеем 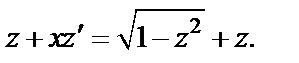
Далее приводим подобные и разделяем переменные, считая 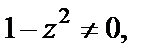 т. е.
т. е. 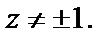 Получаем
Получаем 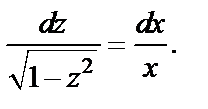 Интегрируем и получаем
Интегрируем и получаем 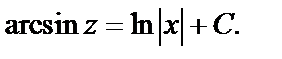
Возвращаемся к старым переменным, получаем общее решение:
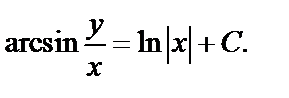
Анализируем, являются ли решениями 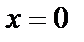 и
и 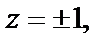 т. е.
т. е. 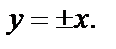 Подставляем
Подставляем 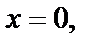
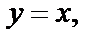
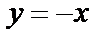 в заданное дифференциальное уравнение и убеждаемся, что
в заданное дифференциальное уравнение и убеждаемся, что 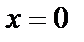 не является решением заданного дифференциального уравнения, а
не является решением заданного дифференциального уравнения, а 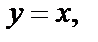
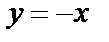 являются решениями, которые не входят в полученное общее решение. Приходим к решению исходного дифференциального уравнения:
являются решениями, которые не входят в полученное общее решение. Приходим к решению исходного дифференциального уравнения:
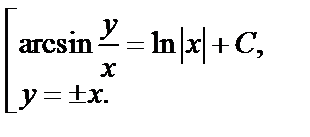
3) Запишем заданное уравнение в виде
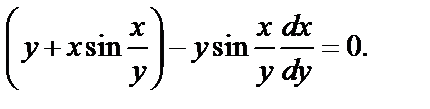
Делим его на y 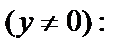
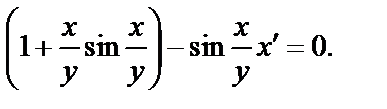 (7.2)
(7.2)
Делаем замену 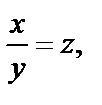 где
где 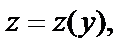 т. е.
т. е. 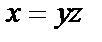 и
и 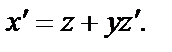 После подстановки в уравнение (7.2) получаем:
После подстановки в уравнение (7.2) получаем:
 т. е.
т. е.
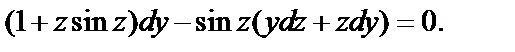
После упрощения имеем 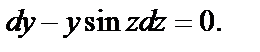
Делим переменные: 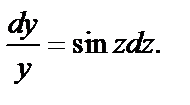
Интегрирование дает:
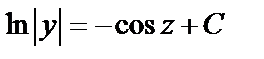 или
или 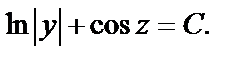
Возвращаемся к старым переменным, используя 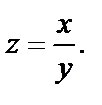 Тогда общий интеграл имеет вид:
Тогда общий интеграл имеет вид: 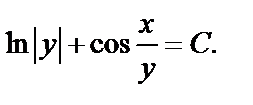
Пример 7.4. Решить задачу Коши:
1) 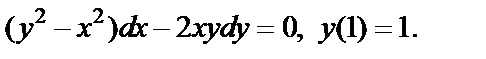
2) 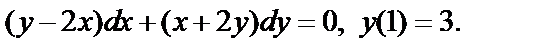
Решение 1) Это однородное уравнение. Разделив заданное уравнение на 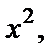
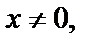 получаем:
получаем:
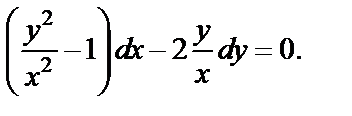
Делаем замену 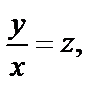
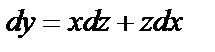 где
где 

или, приведя подобные,
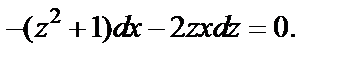
Разделяем переменные:
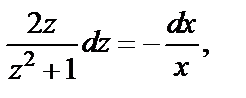
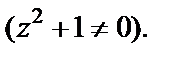
Интегрируем последнее уравнение:
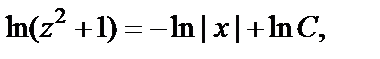
т. е., используя свойства логарифма, имеем 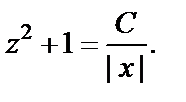
Возвращаясь к старым переменным, получаем: 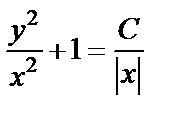 – общий интеграл исходного уравнения.
– общий интеграл исходного уравнения.
Подставляем в него начальные условия 
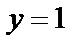 и находим С:
и находим С:
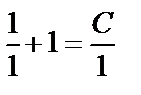 или
или 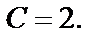
Значит, решением задачи Коши является
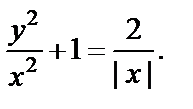
2) Это уравнение однородное. Разделив его на x 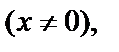 получаем:
получаем:
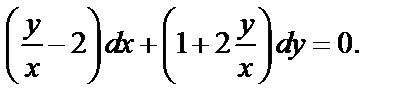
Делаем замену 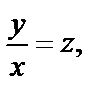 где
где 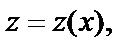
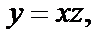
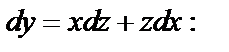
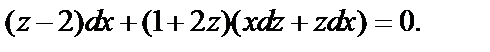
Приводим подобные:
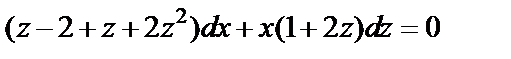 или
или
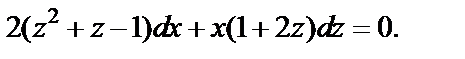
Разделяем переменные, считая 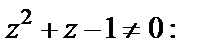
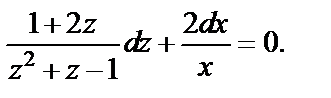 (7)
(7)
Далее интегрируем уравнение (7) и получаем:
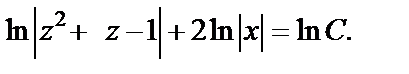
Используем свойства логарифма и получаем: 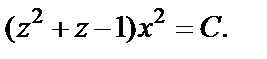
Возвращаемся к старым переменным:
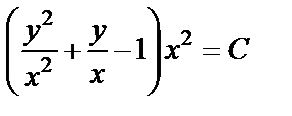 или
или 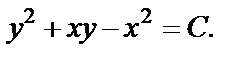
Отсюда получаем:
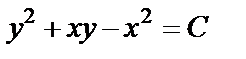 – общий интеграл заданного уравнения. Подставив в него начальные условия:
– общий интеграл заданного уравнения. Подставив в него начальные условия: 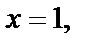
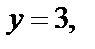 получим
получим 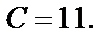
Решение задачи Коши: 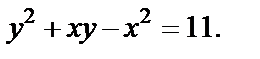
Дифференциальным уравнением второго порядка называется уравнение относительно независимой переменой, искомой функции, ее первой и второй производной. В общем виде это уравнение можно записать так:
F (x, y, y /, у //) = 0.
Задача Коши для дифференциального уравнения второго порядка ставится следующим образом: найти частное решение у = у(х), удовлетворяющее начальным условиям у(х0) = у0, у / (х0) = у0/.
Если уравнение F (x, y, y /, у //) = 0 разрешимо относительно старшей производной, то его можно представить в виде
у // = f (х, у, у /).
К простейшим интегрируемым дифференциальным уравнениям второго порядка относятся уравнения, для которых функция, стоящая в правой части равенства, зависит только от одного из аргументов.
Рассмотрим неполное дифференциальное уравнение второго порядка вида
у // = f (х).
Общее решение этого уравнения находится двукратным интегрированием.
Пример 7.5. Решить задачу Коши:
y // = 36х 5, y /(1) = 12, у(1) = 7.
Решение y // = 36х 5,
y / = 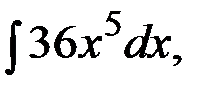
y / = 6х 6 + С1,
y = 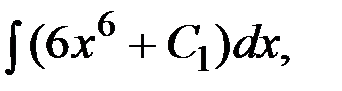
y = 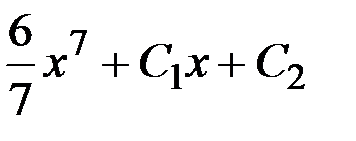 – общее решение.
– общее решение.
Решим задачу Коши, найдя значение С 1 и С 2, удовлетворяющие заданным начальным условиям y /(1) = 12, у(1) = 7:
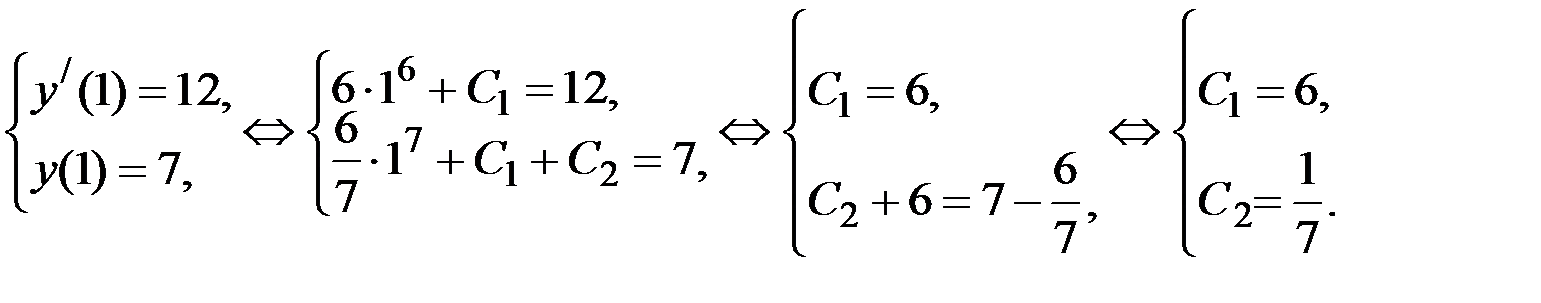
Подставив в общее решение найденные значения С 1 и С2, получим частное решение дифференциального уравнения: у = 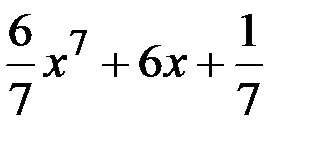 .
.
Ответ: у = 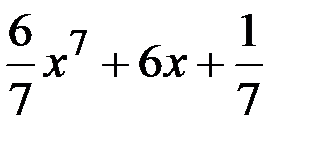 .
.
Пример 7.6. Найти общее решение дифференциального уравнения
у // = (2х + 1)4.
Решениеу // = (2х + 1)4,
у / = 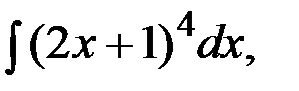
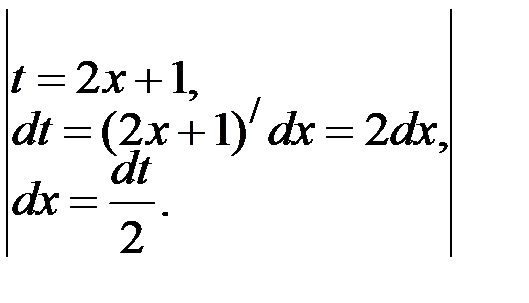
у / = 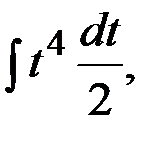
у / = 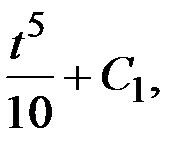
у / = 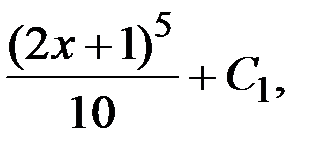
у = 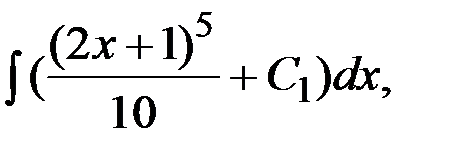
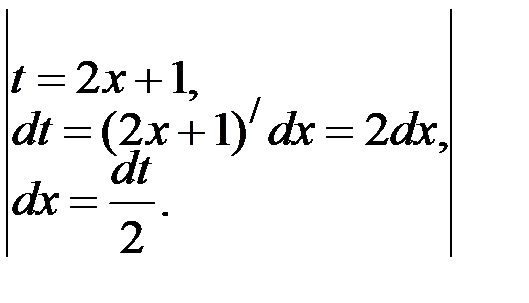
у = 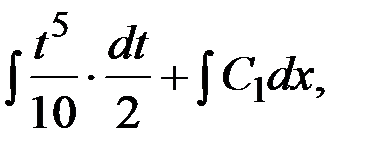
у = 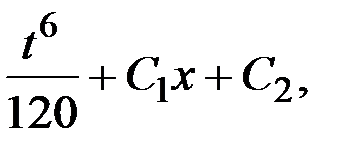
у = 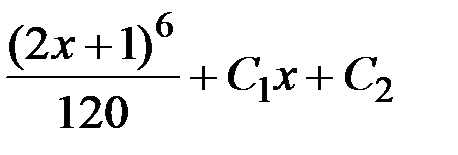 – общее решение.
– общее решение.
Уравнение вида
у // + py / + qy = 0,
где р и q – постоянные (р 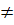 0), называется линейным однородным дифференциальным уравнением (ЛОДУ) II порядка с постоянными коэффициентами вида.
0), называется линейным однородным дифференциальным уравнением (ЛОДУ) II порядка с постоянными коэффициентами вида.
Для его решения составляется характеристическое уравнение, выполнив замены: у //→ k 2, y / → k, y → 1:
k 2 + pk + q = 0
В зависимости от найденных корней характеристического уравнения общее решение дифференциального уравнения имеет вид:
| Дискриминант | Корни характеристического уравнения | Общее решение ЛОДУ II порядка |
| D > 0 | k1 ≠ k2 є R | y = C1 e k x + C2 e k x |
| D = 0 | k1 = k2 = k є R | y = C1 e k x + xC2 e k x |
| D < 0 | k1 = a + bi k2 = a – bi | y = e ax (С1сos bx + С2sin bx) |
Пример 7.7. Решить задачу Коши:
y // - 3y /+ 2y = 0, y /(0) = - 1, у(0) = 3.
РешениеСоставим соответствующее характеристическое уравнение:
k 2 – 3k + 2 = 0
D = 1
k1 = 2, k2 = 1
Тогда общее решение дифференциального уравнения имеет вид
y = C1 e 2x + C2 e x. (1)
Решим задачу Коши, найдя значение С 1 и С 2, удовлетворяющие заданным начальным условиям y /(0) = - 1, у(0) = 3. Но для этого сначала найдем у /, продифференцировав (1):
y/ = 2C1 e 2x + C2 e x
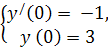
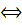
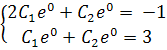
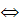
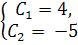
\Подставив в общее решение найденные значения С 1 и С2, получим
частное решение дифференциального уравнения: y = 4e 2x – 5e x.
Ответ: y = 4e 2x – 5e x
Контрольные вопросы
1. Что называется дифференциальным уравнением?
2. Как определяется порядок дифференциального уравнения?
3. Что называется решением дифференциального уравнения?
4. Что называется общим решением дифференциального уравнения?
5. Что называется частным решением дифференциального уравнения?
6. Что значит решить задачу Коши?
7. Что называется дифференциальным уравнением первого прядка?
8. Что значит решить задачу Коши?
9. Что называется дифференциальным уравнением 1 порядка с
разделяющимися переменными?
10. Как решается ДУ 1 порядка с разделяющимися переменными?
11. Какое дифференциальное уравнение 1 порядка называется однородным?
12. Как решается однородное ДУ 1 порядка?
13. Что называется дифференциальным уравнением второго прядка?
14. Какое дифференциальное уравнение называется неполным?
15. Как решается неполное ДУ II порядка?
16. Как решаются линейные однородные дифференциальные уравнения II порядка с постоянными коэффициентами
