Теория вероятности и математическая статистика

По данной теме ознакомьтесь с методическими указаниями по этой теме и внимательно разберите решение примеров из данного пособия. Выполните упражнения для самопроверки.

Элементы теории вероятностей.

Основные понятия комбинаторики. Задачи, при решении которых приходится составлять различные комбинации из конечного числа элементов и производить подсчет числа всех возможных таких комбинаций, называются комбинаторными.

Этот раздел математики находит широкое практическое применение во многих вопросах естествознания и техники.

Размещения. Пусть имеется множество, содержащее n элементов. Каждое его упорядоченное подмножество, содержащее по m элементов, называется размещением из n элементов по m элементов.

Из определения вытекает, что 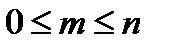и что размещения из n элементов по m – это m-элементные подмножества, отличающиеся составом элементов или порядком их следования.

Число размещений из n элементов по m элементов в каждом обозначаются 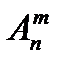и вычисляются по формуле .

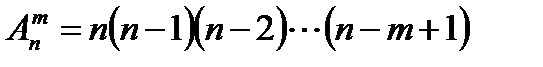Число размещений из n элементов по m элементов в каждом равно произведению m последовательно убывающих натуральных чисел, из которых большее есть n.

Для кратности произведения первых n натуральных чисел принято обозначать 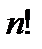(n-факториал):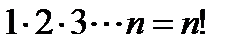

Условились считать, что .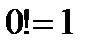

Тогда формулу числа размещений из n элементов по m элементов можно записать в другом виде: .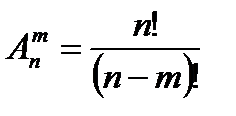

Условились считать, что .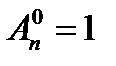

Пример 1. Сколькими способами из группы, включающей 25 студентов, можно выбрать актив группы в составе старосты, заместителя старосты и профорга?

Решение. Состав актива группы является упорядоченным множеством из 25 элементов по три элемента. Значит. Искомое число способов равно числу размещений из 25 элементов по три элемента в каждом: 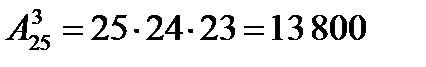, или .

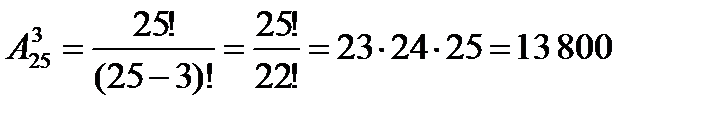Пример 2. Перед выпуском группа студентов в 30 человек обменялась фотографиями. Сколько всего было роздано фотографий?

Решение. Передача фотографии одним студентом другому есть размещение из 30 элементов по два элемента. Искомое число фотографий равно числу размещений из 30 элементов по два элемента в каждом: .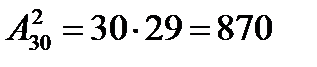

Перестановки. Размещения из n элементов по n элементов называются перестановками из n элементов.

Из определения следует, что перестановки являются частным случаем размещений. Так как каждая перестановка содержит все n элементов множества, то различные перестановки отличаются друг от друга только порядком элементов.

Число перестановок из n элементов данного множества обозначают 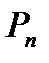и вычисляют по формуле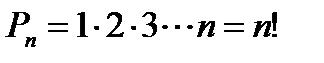

Пример 3. Сколько четырехзначных чисел можно составить из цифр 1, 2, 3, 4 без повторений?

Решение. По условию дано множество из четырех элементов, которые требуется расположить в определенным порядке. Значит, требуется найти количество перестановок из четырех элементов: 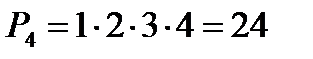, т.е. из цифр 1. 2, 3, 4 можно составить 24 четырехзначных числа (без повторений цифр)

Пример 4. Сколькими способами можно рассадить 10 гостей по десяти местам за праздничным столом?

Решение. Искомое число способов равно числу перестановок из десяти элементов: .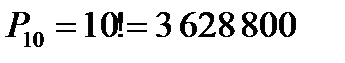

Сочетания. Пусть имеется множество, состоящее из n элементов. Каждое его подмножество, состоящее из m элементов, называется сочетанием из n элементов по m элементов.

Таким образом, сочетания из n элементов по m элементов – это все m-элементные подмножества n-элементного множества, причем различными множествами считаются только те, которые имеют неодинаковый состав элементов.

Подмножества, отличающиеся друг от друга порядком следования элементов, не считаются различными.

Число подмножеств по m элементов в каждом, содержащихся во множестве из n элементов, т.е. число сочетаний из n элементов по m элементов в каждом, обозначают 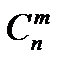и вычисляют по формуле: 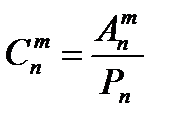или .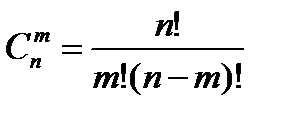

Число сочетаний 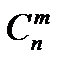обладает следующим свойством: ( ).

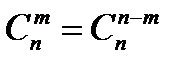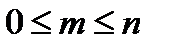Так, .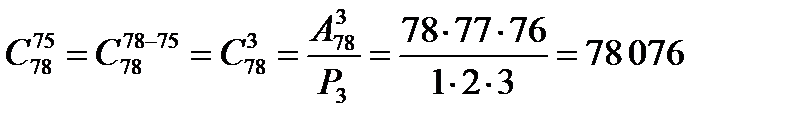

Пример 5. Сколько всего игр должны провести 20 футбольных команд в однокруговом чемпионате?

Решение. Так как игра любой команды A с командой B совпадает с игрой команды B с командой A, то каждая игра есть сочетание из 20 элементов по 2. искомое число всех игр равно числу сочетаний из 20 элементов по 2 элемента в каждом: .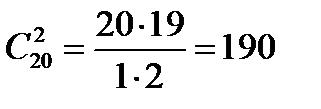

Пример 6. Сколькими способами можно распределить 12 человек по бригадам, если в каждой бригаде по 6 человек?

Решение. Состав каждой бригады является конечным множеством из 12 элементов по 6. значит, искомое число способов равно числу сочетаний из 12 элементов по 6 в каждом: .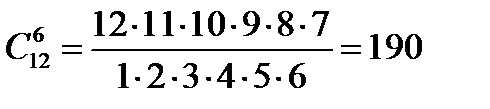

Случайные события. Вероятность события. Теория вероятностей – это математическая наука, которая изучает закономерности в случайных событиях. К основным понятиям теории вероятностей относятся испытания и события.

Под испытанием (опытом) понимают реализацию данного комплекса условий, в результате которого непрерывно произойдет какое-либо событие.

Например, бросание монеты – испытание; появление герба ил и цифры – события.

Случайным событием называется событие, связанное с данным испытанием, которое при осуществлении испытания может произойти, а может и не произойти. Слово «случайное» для краткости часто опускают и говорят просто «событие». Например, выстрел по цели – это опыт, случайные события в этом опыте – попадание в цель или промах.

Событие в данных условиях называется достоверным, если в результате опыта оно непрерывно должно произойти, и невозможным, если оно заведомо не произойдет. Например, выпадение не более шести очков при бросании одной игральной кости – достоверное событие; выпадение десяти очков при бросании одной игральной кости – невозможное событие.

События называются несовместимыми, если никакие два из них не могут появится вместе. Например, попадание и промах при одном выстреле – это несовместимые события.

Говорят, что несколько событий в данном опыте образуют полную систему событий, если в результате опыта непременно должно произойти хотя бы одно из них. Например, при бросании игральной кости события, состоящие в выпадении одного, двух, трех, четырех, пяти и шести очков, образуют полную группу событий.

События называются равновозможными, если ни одно из них не является объективно более возможным, чем другие. Например, при бросании монеты выпадение герба или числа – события равновозможные.

Каждое событие обладает какой-то степенью возможности. Числовая мера степени объективной возможности события – это вероятность события. Вероятность события A обозначается P(A).

Пусть из системы n несовместных равновозможныхисходов испытания m исходов благоприятствуют событию A. Тогда вероятностью события A называют отношение m числа исходов, благоприятствующих событию A, к числу всех исходов данного испытания: .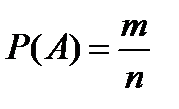

Эта формула носит название классического определения вероятности.

Если B – достоверное событие, то n=m и P(B)=1; если С – невозможное событие, то m=0 и P(С)=0; если A – случайное событие, то 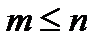и .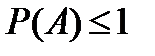

Таким образом, вероятность события заключается в следующих пределах: .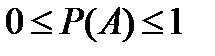

Пример 7. Игральную кость подбрасывают один раз. Найти вероятность событий: A – появление четного числа очков; B – появление не менее пяти очков; C – появление не более пяти очков.

Решение. Опыт имеет шесть равновозможных независимых исходов (появление одного, двух, трех, четырех, пяти и шести очков), образующих полную систему.

Событию A благоприятствуют три исхода (выпадение двух, четырех и шести очков), поэтому 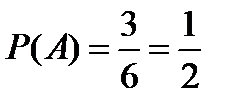; событию B – два исхода (выпадение пяти и шести очков), поэтому 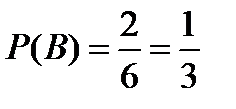; событию C – пять исходов (выпадение одного, двух, трех, четырех, пяти очков), поэтому .

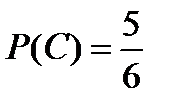При вычислении вероятности часто приходится использовать формулы комбинаторики.

Рассмотрим примеры непосредственного вычисления вероятностей.

Пример 8.В урне 7 красных шаров и 6 синих шаров. Из урны одновременно вынимают два шара. Какова вероятность того, что оба шара красные (событие A)?

Решение. Число равновозможных независимых исходов равно .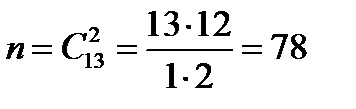

Событию A благоприятствуют 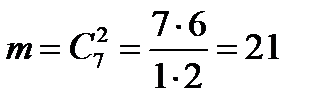исходов. Следовательно, .

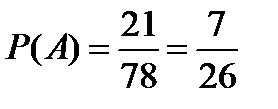Пример 9. В партии из 24 деталей пять бракованных. Из партии выбирают наугад 6 деталей. Найти вероятность того, что среди этих 6 деталей окажутся 2 бракованных (событие B)?

Решение. Число равновозможных независимых исходов равно .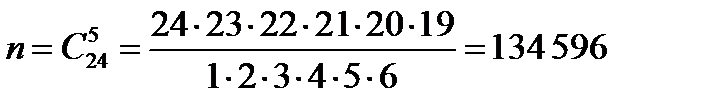

Подсчитаем число исходов m, благоприятствующих событию B. Среди шести взятых наугад деталей должно быть 2 бракованных и 4 стандартных. Две бракованные детали из пяти можно выбрать 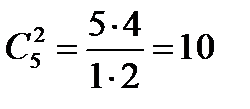способами, а 4 стандартных детали из 19 стандартных деталей можно выбрать 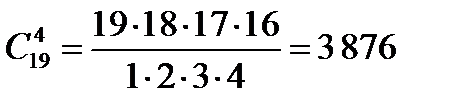способами.

Каждая комбинация бракованных деталей может сочетаться с каждой комбинацией стандартных деталей, поэтому 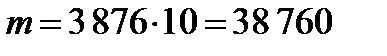. Следовательно, .

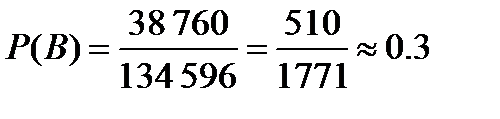Пример 10. Девять различных книг расставлены наудачу на одной полке. Найти вероятность того, что четыре определенные книг окажутся поставленными рядом (событие С)?

Решение. Здесь число равновозможных независимых исходов есть 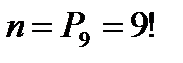. Подсчитаем число исходов т, благоприятствующих событию С. Представим себе, что четыре определенные книги связаны вместе, тогда связку можно расположить на полке 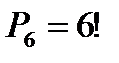способами (вязка плюс остальные пять книг). Внутри связки четыре книги можно переставлять 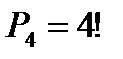способами. При этом каждая комбинация внутри связки может сочетаться с каждым из 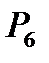способов образования связки, т.е. 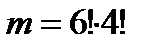. Следовательно, .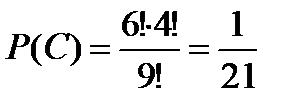