Разложение определителя по элементам строки или столбца

Пример

Задание. Вычислить определитель 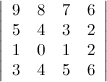, разложив его по элементам какой-то строки или какого-то столбца.

Решение. Предварительно выполним элементарные преобразования над строками определителя, сделав как можно больше нулей либо в строке, либо в столбце. Для этого вначале от первой строки отнимем девять третьих, от второй - пять третьих и от четвертой - три третьих строки, получаем:

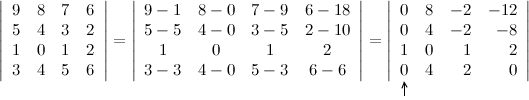
Полученный определитель разложим по элементам первого столбца:

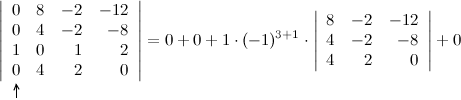
Полученный определитель третьего порядка также разложим по элементам строки и столбца, предварительно получив нули, например, в первом столбце. Для этого от первой строки отнимаем две вторые строки, а от третьей - вторую:

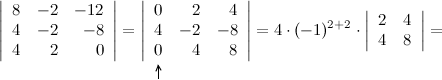
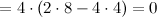
Ответ.

Замечание

Последний и предпоследний определители можно было бы и не вычислять, а сразу сделать вывод о том, что они равны нулю, так как содержат пропорциональные строки.

Приведение определителя к треугольному виду

С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его значение, согласно свойствам определителя, равно произведению элементов стоящих на главной диагонали.

Пример

Задание. Вычислить определитель 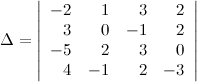приведением его к треугольному виду.

Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования будет выполнять проще, если элемент 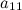будет равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя, приведет к тому, что он сменит знак на противоположный:

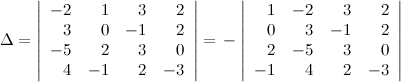
Далее получим нули в первом столбце, кроме элемента 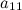, для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:

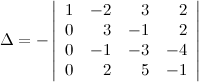
Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если диагональный элемент будет равен 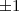, то вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на противоположный знак определителя):

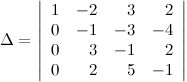
Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом: к третьей строке прибавляем три вторых, а к четвертой - две вторых строки, получаем:

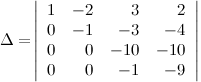
Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под главной диагональю, а для этого к последней строке прибавляем третью:

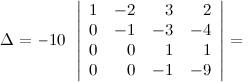
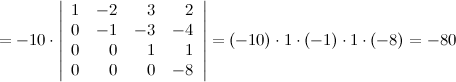
Ответ.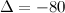

Теорема Лапласа

Теорема

Пусть 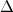- определитель 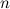-го порядка. Выберем в нем произвольные 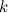строк (или столбцов), причем 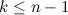. Тогда сумма произведений всех миноров 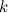-го порядка, которые содержатся в выбранных 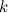строках (столбцах), на их алгебраические дополнения равна определителю.

Пример

Задание. Используя теорему Лапласа, вычислить определитель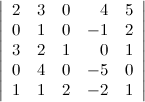

Решение. Выберем в данном определителе пятого порядка две строки - вторую и третью, тогда получаем (слагаемые, которые равны нулю, опускаем):

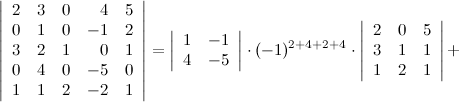
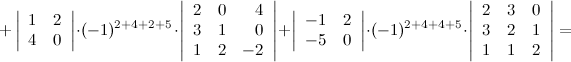
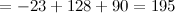
Ответ.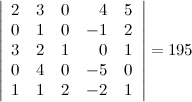

Обратная матрица

На множестве матриц не определена операция деления, она заменена умножением на обратную матрицу.

Определение

Невырожденной называется квадратная матрица, определитель которой не равен нулю. Квадратная матрица называется вырожденной, если ее определитель равен нулю.

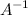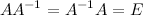Квадратная матрица называется обратной к невырожденной матрице , если , где 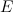- это единичная матрица соответствующего порядка.

Замечание

Обратная матрица существует только для квадратных матриц с не равными нулюопределителями.

Свойства обратной матрицы:

1°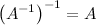

2°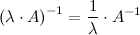

3°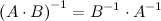

4°