Оценка параметров нелинейной парной регрессии

Оценка параметров нелинейной парной регрессии на основании результатов измерения зависимости напряжения сигнального тока от силы тока в данной работе проводиться с применением команды «Добавить линию тренда» табличного процессора.

Команда «Добавить линию тренда»используется для выделения тренда (медленных изменений) при анализе временных рядов. Однако эту команду можно использовать и для построения уравнения нелинейной регрессии, рассматривая в качестве времени t независимую переменную x, которая является значением силы тока (I).

Эта команда позволяет построить уравнения регрессии различного вида. Но в рамках данной работы требуется только следующие виды:

- линейная;

- экспоненциальная;

- полиноминальная.

Для построения уравнения регрессии необходимо выполнить следующие шаги:

Шаг 1. Ввести по столбцам исходные данные.

Шаг 2. По этим данным построить график в декартовой системе координат.

Шаг 3. Установить курсор на любую точку построенного графика, сделать щелчок правой кнопкой и в появившемся контекстном меню выполнить команду Добавить линию тренда.

Шаг 4. В появившемся диалоговом окне выбрать нужное уравнение регрессии (рисунок 23).

Шаг 5. Включить необходимые опции:

«Показать уравнение на диаграмме»‒ на диаграмме будет показано выбранное уравнение регрессии с вычисленными коэффициентами;

«Поместить на диаграмму величину достоверности аппроксимации (R²)»‒ на диаграмме будет показано значение коэффициента детерминации(для нелинейной регрессии ‒ индекс детерминации R²).

Если по построенному уравнению регрессии необходимо выполнить прогноз, то нужно указать число периодов прогноза.

Шаг 6. После задания всех перечисленных опций на диаграмме появится формула построенного уравнения регрессии и значение индекса детерминации R².

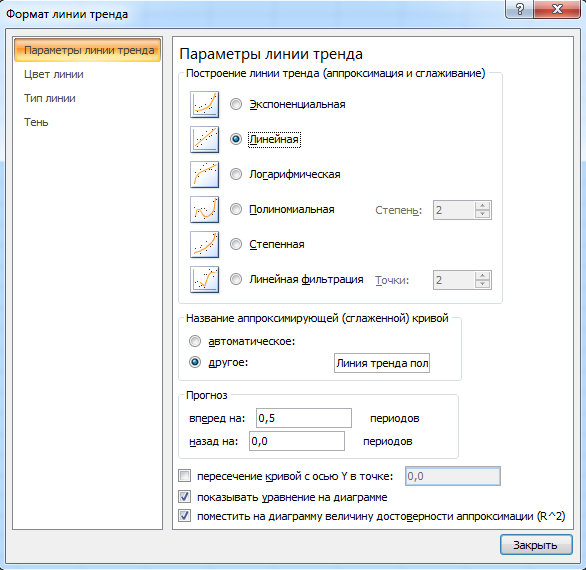
Рисунок 23. Настройка параметров линии тренда
в табличном процессоре MS Excel

При использовании приведенных выше шагов для построения линии тренда линейной регрессии (рисунок 24) коэффициент детерминации (R²) равен 0,023, а уравнение имеет вид:

.

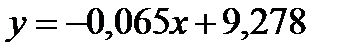Эти результаты подтверждают результаты, полученные при оценке параметров линейной регрессии в параграфе 2.1.

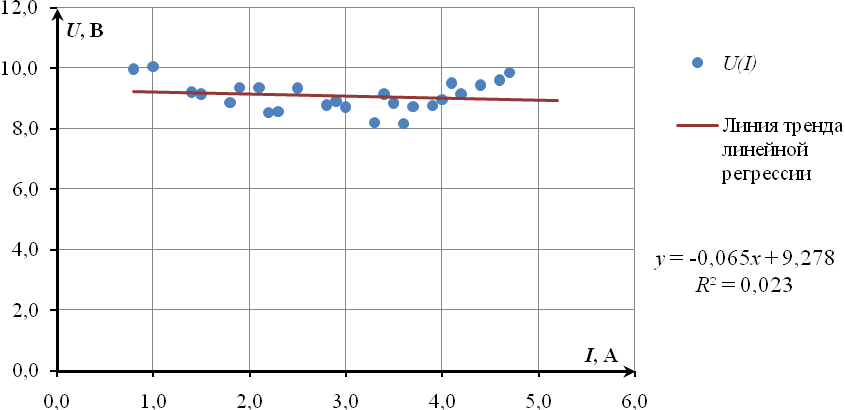
Рисунок 24. График зависимости U(I) с линией тренда линейной регрессии

График линии тренда экспоненциальной регрессии, уравнение этой линии и значение коэффициента детерминации приведен на рисунке 25.

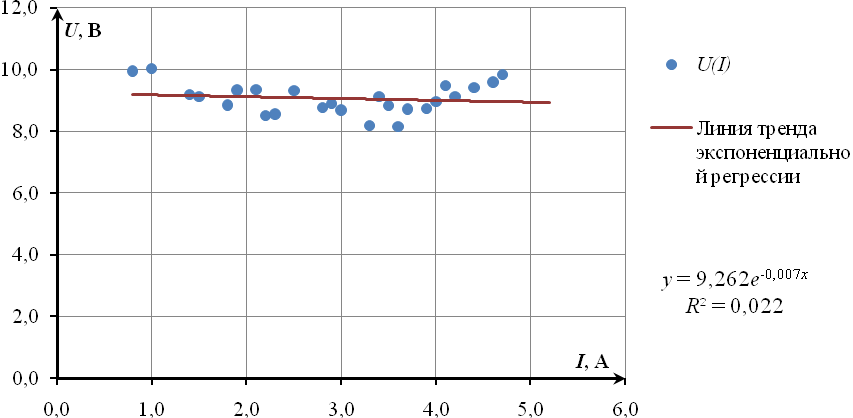
Рисунок 25. График зависимости U(I) с линией тренда экспоненциальной регрессии

Для построения линии тренда полиноминальной регрессии используется степень полинома равная 2. График линии тренда полиноминальной регрессии, уравнение этой линии и значение коэффициента детерминации приведен на рисунке 26.

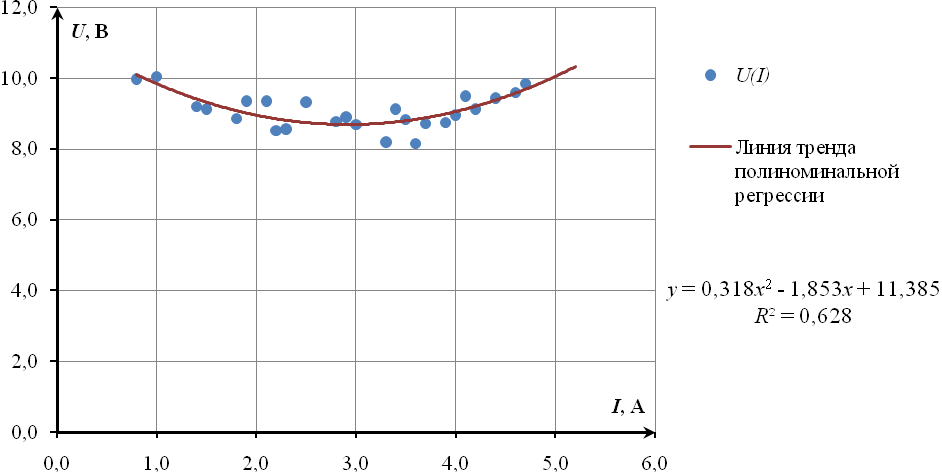
Рисунок 26. График зависимости U(I) с линией тренда полиномиальной регрессии