Задача 1. расчет цепи постоянного тока

МЕТОДИЧЕСКИЕ УКАЗАНИЯ И КОНТРОЛЬНЫЕ ЗАДАНИЯ

к расчетно-графическим работам по теме «Цепи постоянного и синусоидального тока»

курса «Электротехника и электроника»

ВВЕДЕНИЕ

Методические указания и задания составлены для выполнения расчетно-графических работ (РГР), в первую из которых, как правило, входит задание на расчет электрических цепей постоянного тока (задача 1), а во вторую – расчет электрических цепей переменного тока (задачи 2 и 3). Разбивка эта на две РГР представляется условно традиционной, и каждая из задач может быть выдана студентам как отдельная РГР или все три задачи объединены в одну РГР, так как для некоторых специальностей предполагаются еще задания по переходным процессам, электронике и так далее. Преподаватель может задать все пункты перечня заданий к каждой задаче или выбрать пункты по своему усмотрению, может разным студентам предложить расчет разными методами или, наоборот, предложить выбрать наиболее рациональный метод, по мнению самого студента, с соответствующим обоснованием.

К задачам даны методические указания в виде примеров расчета. Наиболее полно разобран пример к задаче 1. В задаче 2 рассмотрены только особенности использования комплексных напряжений, токов, сопротивлений на примере расчета методом преобразования и, наконец, для трехфазных цепей рассмотрен только наиболее сложный случай из заданных: расчет соединения неоднородной нагрузки звездой без нулевого провода. Составитель, однако, считает, что студент вправе рассчитать режим этой цепи любым знакомым ему методом. Например, методом контурных токов, если на то не будет специальных указаний преподавателя, выдавшего РГР. Остальные случаи конфигурации трехфазной цепи (с нейтральным проводом, короткое замыкание или обрыв фазы) рассчитываются слишком просто, чтобы требовались специальные методические указания. Это относится и к векторно-топографической диаграмме, построение которой в общем случае рассмотрено в методических указаниях к задаче 2.

Источником идей и примеров с некоторой доработкой составителя являлись в основном методические указания и контрольные задания для студентов-заочников инженерно-технических специальностей по электротехнике, прошедшие многолетнюю «обкатку» в высших учебных заведениях СССР и РФ, и некоторые кафедральные разработки.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЗАДАЧЕ 1

Пример 1

В этом примере вычисления выполнены с использованием широко распространенной программы MathCAD. Соответствующие записи перенесены в текст документа в основном без преобразований и выглядят так же, как в MathCAD. Будем надеется, что студент без труда сопоставит запись E1:=30 с известным ему из программирования выражением «Е1 присвоить значение 30». Кроме того, студенту известно, что в языках программирования довольно часто индексы проставляются «в рост» с основным обозначением величины, так что Е1 в обычном тексте соответствует записи Е₁.

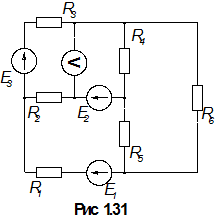Схема электрической цепи и числовые данные представлены ниже:

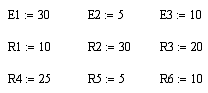Значения ЭДС даны в вольтах, а сопротивлений в Омах.

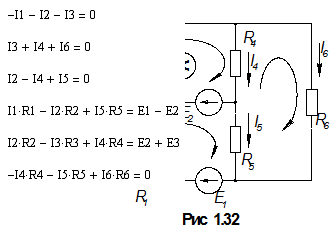Перед составлением уравнения, выберем условные положительные направления токов и положительные направления обходов контуров. Составим уравнения по законам Кирхгофа.

При составлении следим за направлениями токов и ЭДС, и в случае их несовпадения с направлениями обхода контуров приписываем напряжениям, созданным этими токами, знак минус. При составлении уравнений по первому закону Кирхгофа входящие в узел токи (по нашим произвольно направленным стрелкам) считаем положительными, а выходящие из узла пишем со знаком минус. Впрочем, если припишем им противоположные знаки, правильность составления уравнений не нарушится, как не нарушается правильность уравнения при умножении левой и правой частей на минус единицу.

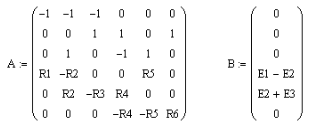Соответствующие этой системе матрицы коэффициентов и свободных членов выглядят так:

Проводим обычные операции для нахождения корней уравнений:

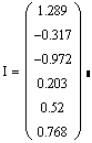Получаем ответ:

Вектор значений токов читается элементами сверху вниз I₁, I₂, I₃, I₄, I₅, I₆, т. е. эту запись надо читать так: I₁ = 1,289 А, I₂ = -0,317 А и т. д.

Систему из шести уравнений с шестью неизвестными решать вручную очень громоздко, поэтому лучше найти возможность использовать ЭВМ. Инструмент MATHCAD, например, имеет в составе своих средств вычислений решение систем алгебраических уравнений несколькими методами.

Один из матричных методов приведен выше, другой метод последовательных приближений используем далее. В последнем случае надо только задать (произвольно) нулевое приближение значений неизвестных токов (в процессе решения системы машиной они будут уточняться до заданной точности) и записать систему уравнений в привычном виде. Перед системой обязательно ключевое слово MATHCAD: «Given»

Затем указываем, как мы решили обозначить неизвестные (или массив неизвестных если их несколько) с ключевым словом «find» – «найти» и перечисляем в скобках имена неизвестных. Вектор неизвестных мы обозначили Strom (по-немецки ток)

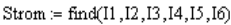И, наконец, «велим» MATHCAD вывести найденные значения на экран (Пишем: Strom =). После чего на экране появляется вектор вычисленных значений:

Здесь сверху вниз по порядку идут значения вычисленных токов: I1, I2 и т. д.

Метод контурных токов

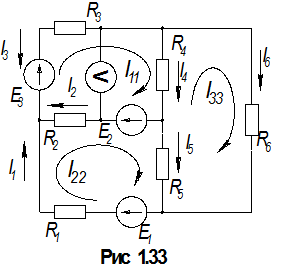Будем считать (в теории доказано, что этот прием приводит к верным результатам), что в каждом контуре течет свой контурный ток. Пусть они совпадают по направлению с уже выбранными направлениями обходов контуров. Чтобы отличить их в обозначениях от токов в ветвях, будет отмечать их двойной индексацией: I_kk, где индекс kkпоказывает номер (k-й) рассматриваемого контура. Представим, что токи в ветвях состоят из контурных токов. Так, во внешних ветвях протекают (при выбранных нами конурах) только по одному контурному току: через сопротивление R₃контурный ток I₁₁, навстречу току I₃. Так что, по-видимому, I₃ = –I₁₁,аналогично I₁ = I₂₂ и I₆ = I₃₃.

Последние пары токов (контурных токов и токов в ветвях) совпадают по направлению, и потому знаки минус отсутствуют.

По сопротивлениям R₂, R₄, R₅ протекают по два контурных тока в противоположных направлениях. Их разности (или алгебраические суммы) и составляют истинные значения силы токов в ветвях.

При составлении алгебраических сумм положительным считается контурный ток, совпадающий по направлению с выбранным изначально положительным направлением тока в ветви. Имеем:

I₂ = I₁₁-I₂₂ , I₄ = I₁₁-I₃₃ и I₅= I₂₂ –I₃₃ .

Таким образом, достаточно нам знать всего три контурных тока для нахождения значения силы токов в ветвях. Значит, если мы сумеем правильно составить систему уравнений относительно контурных токов, то придется решать систему трех уравнений вместо шести. Такую систему уже несложно решать вручную.

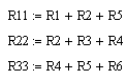Введем понятие собственного сопротивления контура, представляющее сумму всех сопротивлений данного контура (в тексте показаны знаки присваивания, как это записывается в MATHCAD и часто на языках программирования высокого уровня:

Введем также понятие смежного сопротивления контуров, это сопротивление, входящее одновременно в два контура. Смежные сопротивления имеют разные индексы:

Знаки «-» в правой части обусловлены тем, что контурные токи смежных контуров протекают по сопротивлениям R2, R4и R5в противоположные стороны. Если бы мы решили направить обход третьего контура и сам ток I₃₃ против часовой стрелки, то писали бы:

R12 : = -R2, R23 : =R4, R13 : =R5.

Отметим, что всегда:

R21=R12 R32=R23 R31 = R13

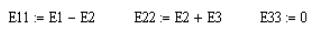Введем понятия контурных ЭДС, представляющие алгебраические суммы всех ЭДС соответствующего контура:

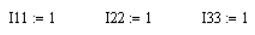Для решения на MATHCAD зададим любые начальные значения контурных токов (например, все по одному амперу):

Составим систему уравнений по методу контурных токов и решим ее.

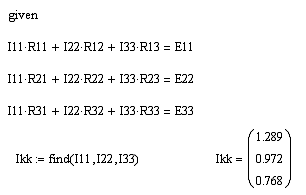Если бы мы не вводили понятий собственных и смежных сопротивлений и контурных ЭДС, то уравнения выглядели бы так:

I11·(R1 + R2 + R5) - I22·R2 - I 33·R5 = E1 - E 2,

-I11 · R2 + I22· (R2 + R3 + R4) - I33·R4 = E2 + E3,

-I11·R5 - I22·R4 + I 33· (R4 + R5 + R6) = 0.

В некоторых случаях такая запись даже более наглядна. Решение системы трех уравнений несложно провести и вручную. Значения контурных токов оказались равными:

I11 = 1,289 А, I22 = 0,972 А, I33 = 0,768 А.

Теперь находим значения силы токов в ветвях:

I1= I11 = 1,289 A , I3 = -I22 = -0,972 A , I6 = I33 = 0,768 A,

I2= I22 - I11 = -0,317 А , I4 = I22 - I33 = 0,204 A , I5 = 0,521 A.

Полученные значения токов совпадают с ранее полученными по законам Кирхгофа.

Метод узловых напряжений (или потенциалов)

Оставим ранее принятые условные положительные направления токов в ветвях. Направления обходов контуров нам теперь не понадобятся.

Обозначим цифрами номера узлов. Выберем точку нулевого потенциала в узле номер 4, т. е. положим φ4=0. Первый этап метода и главная его идея состоят в том, чтобы отыскать потенциалы остальных узлов:φ1, φ2, φ3.

Введем новые обозначения. Будем называть сумму значений роводимостей всех ветвей, подходящих к К-му узлу, узловой проводимостью К-го узла и обозначать Gkk.

Сумму значений проводимостей всех ветвей, соединяющих два узла с номерами k и m, будем обозначать Gkm. Заметим, что в схемах нашего задания каждую пару узлов соединяет не более одной ветви, т. е. в нашем случае Gkm будет представлена всего одним членом.

Кстати, для обозначения потенциалов в учебниках часто используют буквы латинского алфавита V и U. Будем и мы обозначать потенциалы буквой V, оставив U для обозначения напряжений. Тогда потенциалы узлов у нас будут обозначены V1, V2, V3 и V4. Такая замена обозначений не носит принципиального характера. Просто при использовании ЭВМ на написание букв греческого алфавита, как правило, тратится больше времени, а при использовании разных программных инструментов могут встретиться и другие сложности. Кроме того, нам понадобится понятие узлового тока, представляющего собой алгебраическую сумму произведений значений проводимостей ветвей, подходящих к узлу на ЭДС соответствующих ветвей. Если ЭДС направлена от узла, произведение входит в эту сумму со знаком минус. Обозначать узловые токи будем J.

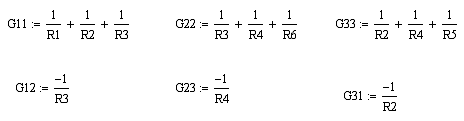Итак:

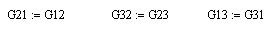Заметим, что:

Узловые токи:

Зададим произвольные начальные значения потенциалов для решения на MATHCAD методом итераций:

Запишем систему уравнений для узловых потенциалов и найдем значения:

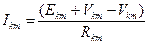Таким образом, мы определили потенциалы узлов в вольтах. Токи в ветвях будем искать по общей формуле:

Здесь I_km, V_km, R_km ток, ЭДС и сопротивление в ветви, соединяющей k-й и m-й узлы. При этом ЭДС E_km считается положительной, если направлена от k-го узла к m-му. В противном случае ее значение пишется со знаком «-». Если же ток оказался отрицательным, то это означает, что он переносит положительные заряды от m-го узла к k-му (или отрицательные в направлении, обозначенном нами стрелкой).

Итак:

I1=I41, I2=I31, I3=I21, I4=I24, I5=I34, I6=I24.

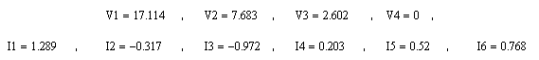Числовые значения, полученные по этим формулам:

Разумеется, здесь значения потенциалов приведены в вольтах, а значения силы токов в амперах.

Метод контурных токов

Для сравнения приведем решение этой же задачи методом контурных токов.

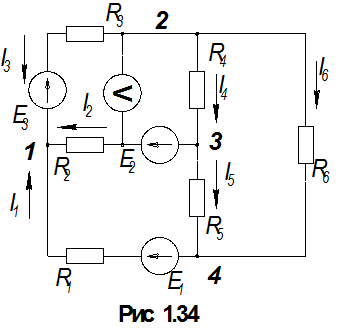
Подготовим схему к составлению уравнений по методу контурных токов. Для этого на схеме (рис. 2.52) надо показать направления обхода контуров и обозначить сами контурные токи.

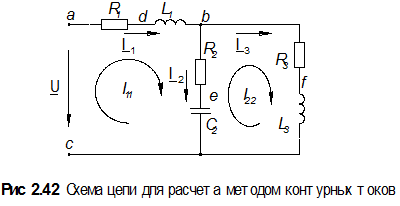Теперь, как и в предыдущей задаче, составляем уравнения, в которые в качестве неизвестных входят контурные токи, а в качестве коэффициентов при них собственные и смежные сопротивления контуров. Разница в том, что и токи, и коэффициенты будут комплексные:

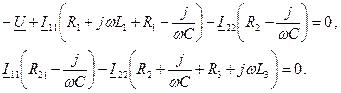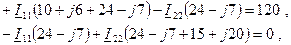Значения активных сопротивлений нам даны в условии задачи, а реактивные сопротивления вычислены при расчетах методом преобразования. Воспользуемся ими и получим уравнения с численными комплексными коэффициентами. Заодно перенесем свободный член -U в правую часть, изменив его знак:

или

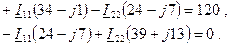Главный определитель системы

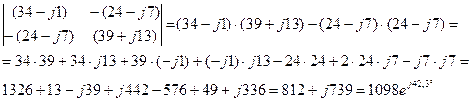
При этих расчетах студенты очень часто забывают, что j·j =j²=-1, и то, что большинство калькуляторов, для вычисления арктангенса используют только результат деления, выдают ответ для первой четверти при положительном результате деления, тогда как при отрицательных значениях одновременно и числителя, и знаменателя значение угла должно лежать в третьей четверти тригонометрического круга. Если же результат деления отрицательный, то калькулятор выдает ответ для угла в четвертой четверти, хотя при отрицательном знаменателе и положительном числителе правильное значение угла находится во второй четверти. За этим приходится следить самому расчетчику и иногда делать дополнительные поправки. Заметим так же, что показатель степени в последнем выражении записан в градусах, хотя с математической точки зрения это не корректно. Формулы преобразования алгебраической формы комплексного числа в показательную предполагают запись аргумента (показателя степени е) в радианах. В литературе же по использованию комплексного метода в электротехнических расчетах такая «вольность» допускается и привилась достаточно широко.

Найдем значения первого и второго определителей, заменив сначала первый столбец в главном определителе на столбец свободных членов, для нахождения второго определителя второй столбец:

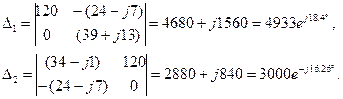
Найдем значения контурных токов и токов в ветвях:

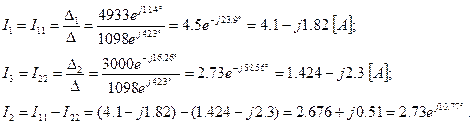
Как видим, отличия очень небольшие, да и те, по-видимому, за счет округлений во время вычислений.

Проверка баланса мощности

Полная комплексная мощность всей цепи равна:

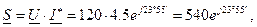
где 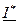– число комплексно-сопряженное комплексу действующего значения тока I₁ , потребляемого от источника.

Для получения I^* - надо изменить знак перед мнимой частью I₁ в алгебраической форме или перед показателем степени е в показательной (экспоненциальной) форме.

Для определения значений активной и реактивной мощностей представим полную комплексную мощность в алгебраической форме. Тогда действительная часть комплекса будет представлять собой активную мощность, а коэффициент при мнимой - реактивную.

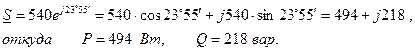
Иная запись этого же действия выглядит так:

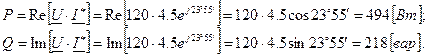
В этом случае Re означает реальную часть комплексного числа (произведения UI^*), а Im - мнимую часть.

Отметим, что значение полной мощности измеряется в вольт-амперах (В·А), а реактивная - в вольт-амперах реактивных (вар).

Значения активной и реактивной мощности можно найти и по-другому, как мощности, потребляемые отдельными потребителями цепи:

P₁ = R₁I₁² = 10-4,5² = 202 Вт; P₂ = R₂I₂² = 180 Вт; P₃ = R₃I₃² = 112 Вт;

Q₁ = X1 I₁² = 6·4,52 = 122 вар; Q₂ = X₂ I₂²= -52,5 вар; Q₃=X₃ I₃² =150 вар.

Проверка показывает, что P = P₁ +P₂+P₃ , что Q≈Q₁+Q₂+Q₃.

Эти равенства значений для активной и реактивной мощностей называются балансом мощности и, в частности, могут служить проверкой правильности решения задачи. Суть в том, что в силу закона сохранения энергии суммы активных и реактивных мощностей, выданных источниками, должна быть равна суммам значений активных и реактивных мощностей, израсходованных потребителями.

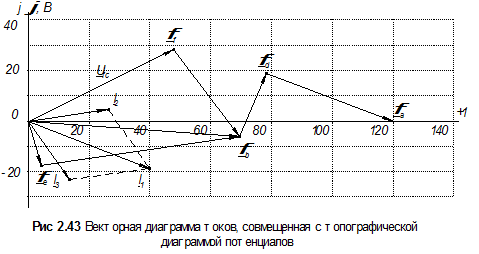
На рисунке (рис. 2.43) приведена векторная диаграмма токов, совмещенная с топографической диаграммой потенциалов цепи. Порядок ее построения следующий.

Строим оси комплексной плоскости: ось действительных (как правило, горизонтальная ось) и ось мнимых (как правило, вертикальная ось). Выбрав удобный масштаб для тока, из начала координат проводим векторы I₁, I₂ и I₃. Можно воспользоваться алгебраической формой записи, откладывая по осям действительные и мнимые части комплексных изображений этих токов, можно использовать показательную форму, тогда вектор, изображающий соответствующий ток 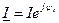, откладывается из начала координат под углом ψ_i к оси действительных (против часовой стрелки, если ψ_i> 0, и по часовой, если ψ_i<0). Это и будет векторной диаграммой токов. Конечно, при правильном решении должен выполняться 1-й закон Кирхгофа в векторной и в комплексной формах: I₁ = I₂ + I₃ или I₁+I₂=I₃.

Топографическая диаграмма напряжений показывает на комплексной плоскости значения комплексных потенциалов всех точек цепи, разделенных какими-либо элементами. Отрезки, соединяющие точки на этой диаграмме, представляют собой векторные изображения на комплексной плоскости напряжений между соответствующими точками цепи. Надо только помнить, что в отличие от стрелок, изображающих напряжение на схеме цепи, векторы напряжений на топографической диаграмме направлены в сторону потенциала, обозначенного первым индексом напряжения. Так, вектор U_ab направлен от точки φ_b к точке φ_a.

Расчет самих комплексных потенциалов ведется почти так, как мы это делали для потенциальной диаграммы в задаче 1. Так, приняв потенциал нижней клеммы источника (или, что тоже, точки С) равным нулю, поместим его в начало координат комплексной плоскости. U_bc=φ_b-φ_c=φ_b. Из последнего ясно, что найденное нами ранее значение U_bc как раз и есть потенциал точки «b» и может быть показан на комплексной плоскости в точке, на которую укажет вектор длиной, соответствующей 68,4В, проведенной под углом -5°30' к оси действительных. Путь тока между точками «b» и «c» может лежать через две ветви, в каждой из которых есть своя точка, потенциал которой отличен как от φ_b, так и от φ_c. Это точки «e» и «f». Их потенциалы можно определить как

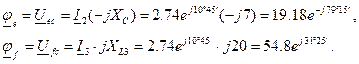
При вычислениях надо помнить, что j = e^{j 90°}, а -j = e ^-j90°. Остается определить положение потенциалов точек «d» и «a». Имеем:

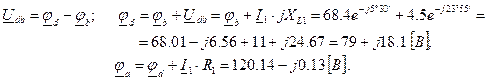
Как видим, мы пришли в точку, лежащую почти на оси действительных на расстоянии, соответствующем 120 В от начала координат (от точки φ). Сюда мы и должны были прийти, если учесть, что напряжение между точками «a» и «c» по условию равно 120 В, а начальную фазу этого входного напряжения мы приняли равной нулю.

ЗАДАЧА 3. РАСЧЕТ ТРЁХФАЗНОЙ ЦЕПИ.

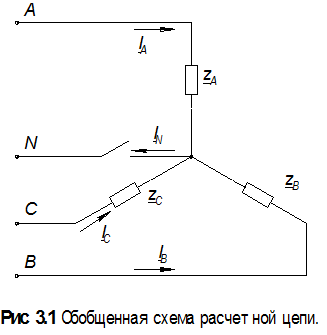1. Выбрать из таблицы 3.1 величины активных и реактивных сопротивлений фаз для цепи, заданной схемой (рис. 3.1).

2. Нарисовать простейшую схему трехфазной цепи с условным изображением активных сопротивлений, индуктивностей и емкостей, соответствующих данным задачи.

3. Рассчитать значения всех токов в цепи с подключенным нейтральным проводом.

4. Рассчитать значения всех токов в цепи при отключении нейтрального провода.

5. Рассчитать значения всех токов при обрыве фазы, указанной, в таблице 3.1 с подключенным нейтральным проводом.

6. Рассчитать значения всех токов при обрыве фазы с отключенным нейтральным проводом.

7. Рассчитать значения всех токов в цепи при коротком замыкании фазы и отключенном нейтральном проводе.

8. Построить векторную диаграмму для рассчитанных в предыдущих пунктах режимов.

9. Подсчитать активную мощность, потребляемую цепью, для рассчитанных режимов.

Таблица 3.1

Вари-анты	Uл В	RА Ом	ХА Ом	RB Ом	ХВ Ом	RC Ом	ХС Ом	Обрыв фазы	КЗ фазы
					-		-	С	В
			-20		-		-	С	В
					-	-		С	В
			-40		-	-		С	В
					-	-	-50	С	В
			-20		-	-	-30	С	В
				-			-	В	С
			-15	-			-	В	С
				-	-30		-	В	С
			-30	-	-40		-	В	С
				-		-		В	С
			-30	-		-		В	С
				-	-50	-		В	С
			-40	-	-50	-		В	С
				-		-	-40	В	С
			-10	-		-	-50	В	С
				-	-20	-	-20	В	С
			-20	-	-15	-	-20	В	С
			-				-	С	А
			-		-15		-	С	А
			-			-		С	А
			-		-15	-		А	С
			-			-	-50	А	С
			-		-40	-		А	С
		-	-20	-			-	А	В
		-					-	А	С
		-	-30				-	А	С
		-			-15		-	А	С
		-					-	А	С
		-				-		С	А
		-		-	-10		-6	В	А
		-	-15	-	-15			В	А
		-	-20	-	-20		-16	В	А
		-		-	-30		-18	В	А
		-		-	-45			В	А
		-				-	-45	В	С
		-	-50		-30	-	-50	А	С
		-	-30	-			-18	А	В
		-		-			-28	В	А
		-		-				В	А

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

Борисов, Ю. М. Электротехника. Учебник для вузов - 2-е изд., перераб. и доп. /Ю. М. Борисов и др. - М.: Энергоатомиздат, 1985 (и все последующие издания).

Касаткин, А. С. Электротехника. Учебное пособие для вузов. - 4-е изд. /

А. С. Касаткин, М. В. Немцов: - М.: Энергоатомиздат, 1983 (и последующие издания).

Бессонов, Л. А. Теоретические основы электротехники /Л. А. Бессонов. - М.: Высшая школа, 1973 (и все последующие издания).

Нейман, Л. Р. Теоретические основы электротехники т.1/Л. Р. Нейман, К. С. Демирчян. - М. - Л.: Энергия, 1965 (и все последующие издания).

СОДЕРЖАНИЕ

ВВЕДЕНИЕ…………………………………………………………

Задача 1. Расчет цепи постоянного тока……………………………

Задача 2. Расчет цепи синусоидального тока………………………

Задача 3. Расчет трехфазной цепи…………………………………

БИБЛИОГРАФИЧЕСКИЙ СПИСОК……………………………….

МЕТОДИЧЕСКИЕ УКАЗАНИЯ И КОНТРОЛЬНЫЕ ЗАДАНИЯ

к расчетно-графическим работам по теме «Цепи постоянного и синусоидального тока»

курса «Электротехника и электроника»

ВВЕДЕНИЕ

Методические указания и задания составлены для выполнения расчетно-графических работ (РГР), в первую из которых, как правило, входит задание на расчет электрических цепей постоянного тока (задача 1), а во вторую – расчет электрических цепей переменного тока (задачи 2 и 3). Разбивка эта на две РГР представляется условно традиционной, и каждая из задач может быть выдана студентам как отдельная РГР или все три задачи объединены в одну РГР, так как для некоторых специальностей предполагаются еще задания по переходным процессам, электронике и так далее. Преподаватель может задать все пункты перечня заданий к каждой задаче или выбрать пункты по своему усмотрению, может разным студентам предложить расчет разными методами или, наоборот, предложить выбрать наиболее рациональный метод, по мнению самого студента, с соответствующим обоснованием.

К задачам даны методические указания в виде примеров расчета. Наиболее полно разобран пример к задаче 1. В задаче 2 рассмотрены только особенности использования комплексных напряжений, токов, сопротивлений на примере расчета методом преобразования и, наконец, для трехфазных цепей рассмотрен только наиболее сложный случай из заданных: расчет соединения неоднородной нагрузки звездой без нулевого провода. Составитель, однако, считает, что студент вправе рассчитать режим этой цепи любым знакомым ему методом. Например, методом контурных токов, если на то не будет специальных указаний преподавателя, выдавшего РГР. Остальные случаи конфигурации трехфазной цепи (с нейтральным проводом, короткое замыкание или обрыв фазы) рассчитываются слишком просто, чтобы требовались специальные методические указания. Это относится и к векторно-топографической диаграмме, построение которой в общем случае рассмотрено в методических указаниях к задаче 2.

Источником идей и примеров с некоторой доработкой составителя являлись в основном методические указания и контрольные задания для студентов-заочников инженерно-технических специальностей по электротехнике, прошедшие многолетнюю «обкатку» в высших учебных заведениях СССР и РФ, и некоторые кафедральные разработки.

ЗАДАЧА 1. РАСЧЕТ ЦЕПИ ПОСТОЯННОГО ТОКА

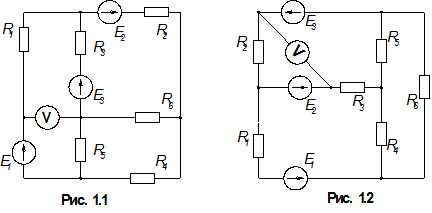
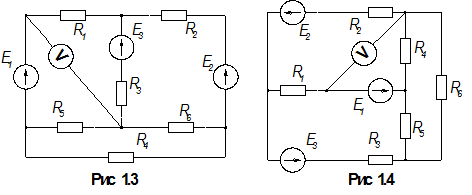
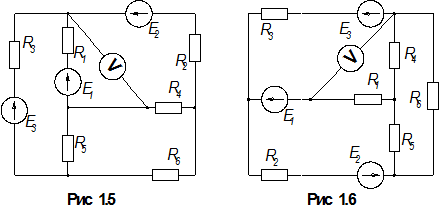
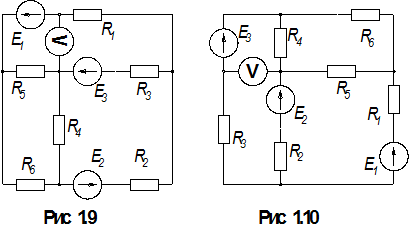
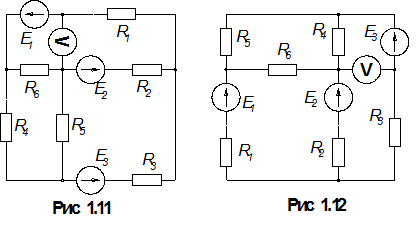
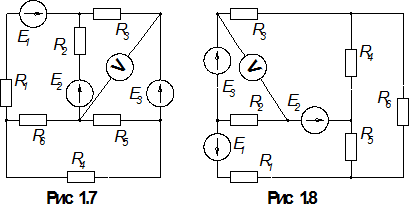
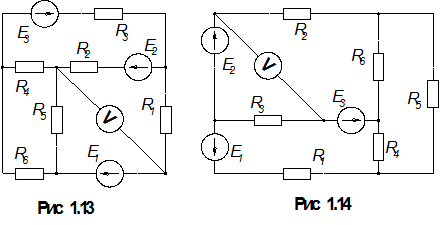
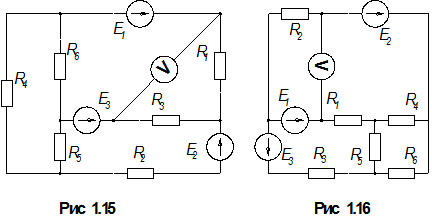
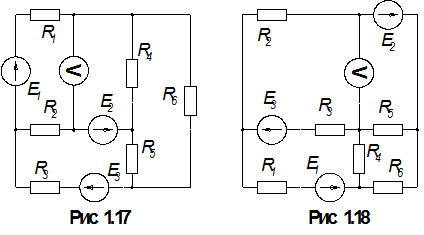
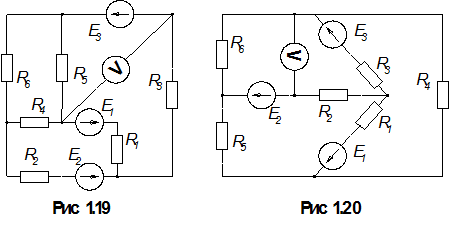
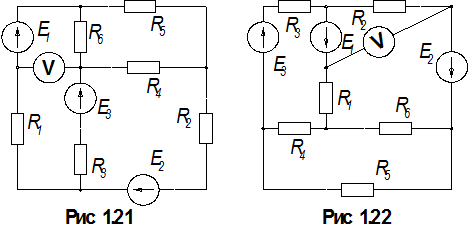
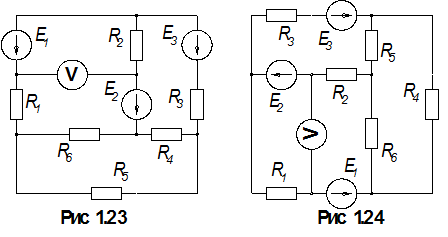
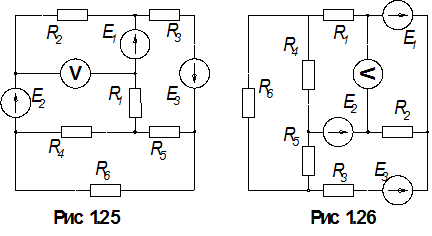
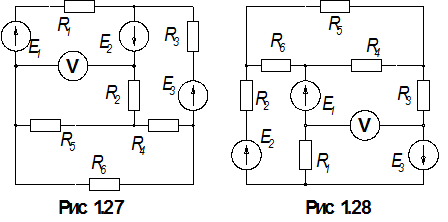
1.По номеру варианта найти в таблице 1.1 схему электрической цепи и параметры ее элементов.

2.Найти все токи тремя способами:

а) используя законы Кирхгофа;

б) методом контурных токов;

в) методом узловых напряжений;

г) ток в шестой ветви методом эквивалентного генератора и свести результаты в единую таблицу.

3. Определить показания вольтметра. Вольтметр на схемах показан окружностью без символов внутри.

4.Составить баланс мощности.

5.Построить в масштабе потенциальную диаграмму для внешнего контура.

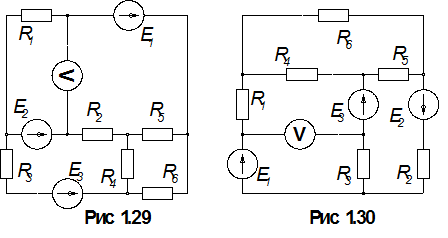Таблица 1.1

Вар.	Рис.	Е1, В	Е2, В	Е3, В	R1, Ом	R2, Ом	R3, Ом	R4, Ом	R5, Ом	R6, Ом
	1.1
	1.2
	1.3
	1.4
	1.5
	1.6
	1.7				3,5
	1.8
	1.9
	1.10				2,7
	1.11
	1.12				2,5
	1.13				4,2
	1.14				3,5
	1.15
	1.16
	1.17
	1.18				2,5
	1.19				3,5
	1.20				4,5
	1.21
	1.22
	1.23
	1.24
	1.25
	1.26
	1.27				1,5
	1.28				1,2
	1.29
	1.30