Представление композиции отношений матрицами и графами

Атрибут – это свойство. При описании каждого из объектов мы должны будем ограничиваться некоторым набором свойств, адекватных решаемой задаче. Изучением этих свойств занимается теория приближенных множеств.

Понятие: – абстрактное П., т.е. понятие, в котором отображен не данный объект (предмет, явление) как таковой, а какой-либо признак объекта, мысленно отделенный от самого объекта.

Пространство решений U - это свойство, которое входит в сферу наших интересов. Каждый элемент этого пространства назовём x_j. Каждый объект пространства U будет обладать свойствами. Если этот объект физический, то его свойства можно обозначить каким-то способом, в результате мы можем получить бесконечное множество свойств. Будем ограничиваться лишь их некоторым подмножеством. Обозначим это подмножество пространства U символом Q. Каждое свойство, принадлежащее этому множеству, обозначим символом q, с соответствующими индексами q_i. Один объект будет отличаться от другого, либо считаться подобным третьему объекту этих свойств. Обозначим символом Vq множество значений, которые может принимать свойство q. Обозначим свойство q объекта x вектором V^xq, а вектор всех свойств объекта - как V:

V= [V^xq₁, V^xq₂, …,V^xq_n]. (1.1)

Всё это можно будет представить в виде информационной системы.

Определение 1: Информационной системой (ИС) называется упорядоченная четверка SI = <U, Q, V, f> (SI – кортеж), где U – множество объектов, Q – множество свойств (атрибутов), V – V_q =U, V_q– множество всех значений и свойств 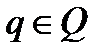, а f: U * Q → U, называется информационной функцией.

Можно записать, что V^xq = f(x, q), очевидно, f(x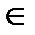, q) V_q.

Равнозначно V^xq = f(q), при которой информационная функция будет интерпретироваться как семейство функций. Тогда f x .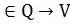

Пример 1: Магазин по продаже автомобилей. В данный момент в продаже находится 10 машин. Пространство решений состоит из 10 объектов, т.е. U = [x₁, x₂, …, x₁₀]. Владелец автомобилей отмечает в своих документах 4 свойства каждого автомобиля, которые являются наиболее часто встречаемыми при продаже. Это количество дверей (q₁), мощность двигателя (q₂), цвет (q₃) и марка (q₄). Таким образом, множество свойств можно представить в виде Q = {q₁, q₂, q₃, q₄}. Необходимо представить в виде таблицы ИС информацию к данному примеру.

Решение:

Объект U	Кол-во дверей q1	Мощность двигателя q2	Цвет q3	Марка q4
X1			Синий	Опель
X2			Черный	Ниссан
X3			Красный	Феррари
X4			Серый	Бугатти
X5			Зеленый	Тойота
X6			Белый	Хонда
X7			Оранжевый	Жигули
X8			Голубой	Мерседес
X9			Золотой	Шкода
X10			Розовый	Рено

В результате, множество значений каждого свойства будет Vq₁ = {2,3,4, …}, Vq₂ = {60, 100, 200, …, 100}, Vq₃ = {черный, синий, белый, …}, Vq₄ = {Феррари, Ниссан, Опель, …}.

Таблицей решений называется упорядоченная пятёрка: DT = <U, C, D, V, f>. Здесь элементы множеств C – условные свойства (атрибуты), элементы множества D – являются регламентирующими свойствами, информационная функция f – характеризует множество правил, содержащихся в таблице решений, в которой каждая функция f_e: 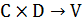(находится) определяет

e–тое решающее правило в таблице. Таблицу решений будем считать способом представления информации, альтернативным по отношению к правилам:

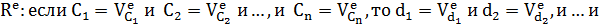
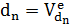- правило «модус – поненс» [7].