Б. Элементы теории множеств, операции над множествами, кванторы
В математике широко используется понятие «множество». Понятие множества настолько общее, что трудно дать ему какое-либо определение, которое не сводилось бы просто к замене слова «множество» равнозначащими выражениями: совокупность, собрание и т.п.
Множество состоит из элементов
Примеры:
N – множество натуральных чисел.
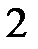 |
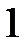 |
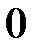 |
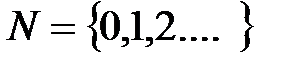
Z – множество целых чисел.
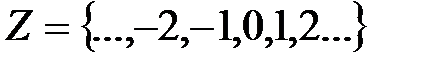
 |
 |
 |
 |
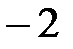 |
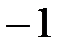 |
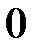 |
R – множество всех точек числовой оси (вещественная числовая ось).
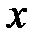 |
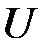 - некоторое полное множество
- некоторое полное множество
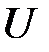 |
Подмножество – часть элементов некоторого множества.
В математике введены символы для обозначения понятий, используемых при рассуждениях.
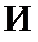 - объединение множеств
- объединение множеств
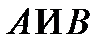 - множество элементов, входящих либо в А, либо в В.
- множество элементов, входящих либо в А, либо в В.
| В |
| А |
Пример:
 ;
; 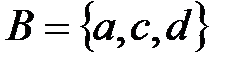
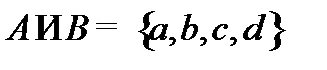
 пишут + : А+В
пишут + : А+В  - пересечение множеств.
- пересечение множеств.
 - множество элементов, входящих одновременно и в А, и в В.
- множество элементов, входящих одновременно и в А, и в В.
| В |
| А |
Например, для рассмотренных нами множеств А и В
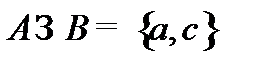
Иногда, вместо  пишут
пишут  : А
: А  В
В
\ - разность множеств
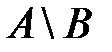 - множество элементо в А, не входящих в В
- множество элементо в А, не входящих в В
| А |
| В |
Например, для рассмотренных нами множеств А и В

Иногда вместо  пишут - : А-В
пишут - : А-В
 - симметричная разность
- симметричная разность
По определению 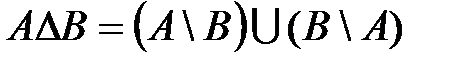
| А |
| В |
Для рассмотренных нами множеств А и В
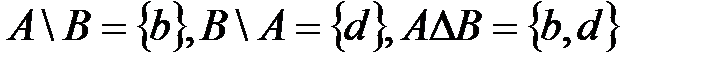
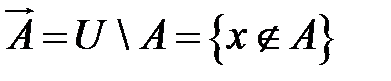 - дополнение к множеству
- дополнение к множеству
| U |
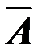 |
| А |
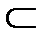 - знак вхождения одного множества в другое
- знак вхождения одного множества в другое
Пример:
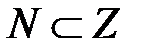
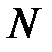 - подмножество множества
- подмножество множества 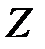

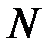 - подмножество числовой оси
- подмножество числовой оси
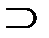 - знак включения одного множества в другое
- знак включения одного множества в другое
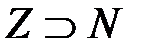
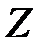 включает в себя множество
включает в себя множество 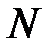
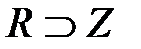 числовая ось включает в себя множество целых чисел
числовая ось включает в себя множество целых чисел
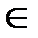 - знак принадлежности элемента множеству
- знак принадлежности элемента множеству
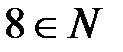 ,
,  ,
, 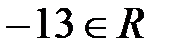
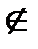 - отрицание принадлежности элемента множеству
- отрицание принадлежности элемента множеству
Примеры:
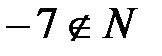 - число -7 не принадлежит множеству натуральных чисел
- число -7 не принадлежит множеству натуральных чисел
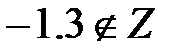 - число -1.3 не принадлежит множеству целых чисел
- число -1.3 не принадлежит множеству целых чисел
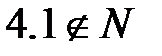 - число 4.1 не является целым числом
- число 4.1 не является целым числом
Ø – пустое множество – множество, в котором нет ни одного элемента
Пример:
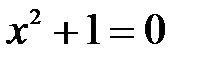 - множество действительных решений этого квадратного уравнения – пусто.
- множество действительных решений этого квадратного уравнения – пусто.
Кванторы
 - для всякого
- для всякого
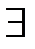 - найдется
- найдется
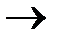 - следует
- следует
~ (тильда) – эквивалентно
 - тождественно
- тождественно
Множества на числовой оси
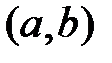 - открытый интервал
- открытый интервал
 |
 |
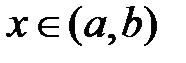 ~
~ 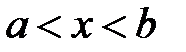
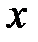 |
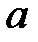 |
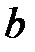 |
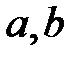 - граничные точки интервала
- граничные точки интервала 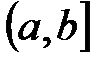 - полуоткрытый слева интервал
- полуоткрытый слева интервал
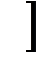 |
 |
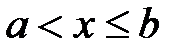
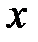 |
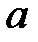 |
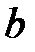 |
Аналогично определяется полуоткрытый справа интервал 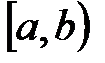
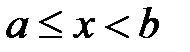
 |
 |
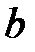 |
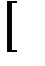 |
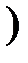 |
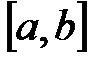 - замкнутый интервал
- замкнутый интервал
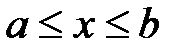
]
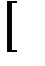 |
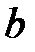 |
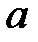 |
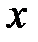 |
Эпсилон окрестность точки “а”
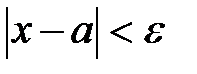 ~
~ 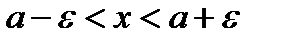
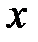 |
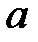 |
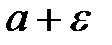 |
 |
 |
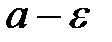 |
Элементы математической логики
p, q –Булевы переменные (принимающие два значения):
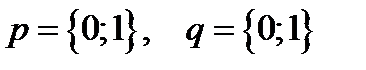
Мы будем рассматривать функции от Булевых переменных, причем эти функции так же будут принимать два значения 0;1.

Некоторые виды функций:
| p | p |
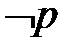 – отрицание
– отрицание
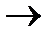 - логическое следствие (p
- логическое следствие (p 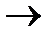 q)
q)
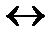 - эквивалентность (p=q), либо (p↔q)
- эквивалентность (p=q), либо (p↔q)
 - конъюнкция p
- конъюнкция p  q (.)
q (.)
 - дизъюнкция p
- дизъюнкция p  q (+)
q (+)
Таблица истинности
| p | q | p  q q | p  q q | p 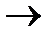 q q | p 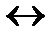 q q |
Используя исходные таблицы истинности, мы сможем строить таблицы истинности для более сложных выражений.
Часть 1.
Глава 1. Математические основы формализации и методов описания
Интеллектуальных технологий информационных систем
