Воспроизведение последовательности значений случайной величины
равномерно распределенной в интервале [0, 1]
Успех применения метода Монте-Карло во многом определяется качеством случайных чисел, используемых в процессе расчета. Случайные числа а, равномерно распределенные в интервале (0, 1), могут быть получены одним из трех методов: табличный метод, метод генерирования с помощью специальных датчиков, метод генерирования программным способом,. Каждый из перечисленных методов имеет свои достоинства и недостатки и свою область применения.
Табличный метод заключается в считывании в определенном порядке (например, подряд) случайных чисел, равномерно распределенных в интервале (0, 1), из специально составленной таблицы. Имеется несколько таблиц a, разработанных как в СССР, так и за рубежом. Качество этих таблиц, т. е. соответствие требованиям, предъявляемым к случайным, равномерно распределенным числам, достаточно высокое. До последнего времени таблицы использовались главным образом при ручных вспомогательных расчетах или в учебных целях. Сейчас, в связи с увеличением оперативной памяти машин и увеличением скорости передачи данных из внешних запоминающих устройств, интерес к табличному методу снова возродился. На первых этапах сами таблицы получались с помощью рулетки, отсюда и название: метод Монте Карло.
Метод датчиков заключается в использовании специальных датчиков, формирующих случайные величины путем физического моделирования некоторых случайных процессов. В качестве датчиков могут выступать различные механические или электронные устройства. На первом этапе использования метода статистических испытаний случайные числа генерировались с помощью различных механических устройств. Например, первые таблицы равномерно распределенных случайных чисел были получены с помощью диска, приводимого во вращательное движение мотором и действующего подобно колесу рулетки.
В настоящее время равномерные случайные числа получаются на некоторых ЭВМ с помощью специального приспособления — «датчика» случайных чисел, который преобразует результаты случайного физического процесса с ЭВМ (шумы электронных ламп и др.) в последовательность двоичных разрядов.
Использование такого датчика повышает скорость вычислений, так как в каждый такт работы ЭВМ в фиксированную стандартную ячейку памяти выдается новое случайное число.
Недостатком генерирования с помощью датчиков является некоторая неустойчивость случайных чисел, связанная, например, с изменением напряжения (случайные числа начинают «течь»). Вследствие этого датчики нуждаются в постоянной профилактической проверке.
Программный метод получил наибольшее распространение. Он заключается в воспроизведении случайных чисел на ЭВМ по одной из специально разработанных программ. Алгоритм этих программ представляет собой некоторое рекуррентное соотношение, по которому каждое последующее значение ai+1 образуется из предыдущих а, и аi-1 путем преобразования, состоящего из арифметических и логических операций. Такая последовательность чисел может удовлетворять различным статистическим критериям случайности. В то же время каждое из чисел последовательности находится с помощью детерминированного математического выражения по предшествующему числу, т. е. не является случайным. С учетом этих двух обстоятельств для чисел, полученных программным способом, было введено название «псевдослучайные». К основным достоинствам программного способа генерирования случайных чисел помимо обстоятельств, связанных с объемом памяти ЭВМ, относится возможность контроля работы ЭВМ в процессе решения задачи (возможность проведения двойного счета), а также простота алгоритма и устойчивость результата счета.
Однако и этот метод имеет некоторые недостатки. Главным недостатком является периодичность «псевдослучайных» чисел. Правда, длина отрезка апериодичности очень велика (108—109), но тем не менее в некоторых случаях даже с практической точки зрения очень длинные последовательности не будут случайными.
Один из наиболее простых способов генерирования псевдослучайных чисел, известный под названием способа средних квадратов, разработан Нейманом. Этот способ состоит в том, что исходное случайное число возводится в квадрат. В качестве следующего случайного числа берется последовательность цифр, стоящих по нумерации разрядов на среднем месте в вычисленном квадрате, содержащая столько же разрядов, сколько и исходное число. Затем это полученное число возводится в квадрат для получения следующего числа и т. д. Этот способ довольно прост и легко реализуется на машине. Вместе с тем он имеет следующие недостатки:
1) если не заменять появившиеся нулевые значения цифр в числах каким-либо другим, то вся дальнейшая последовательность быстро вырождается и в дальнейшем будет состоять из нулей;
2) проверка по статистическим критериям показала, что этот алгоритм дает больше чем нужно малых значений.
Поэтому были разработаны новые алгоритмы, в той или иной мере учитывающие названные недостатки. В частности, широкое распространение получили алгоритмы, основанные на формуле
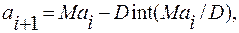
которая при соответствующем подборе целых значений М и D вырабатывает случайные целые числа между 1 и D — 1 [21].
9.5. Моделирование рядов наблюдений поразличным
математическим схемам
