Среднее квадратическое отклонение. Для оценки рассеяния возможных значений случайной величины вокруг ее среднего

Для оценки рассеяния возможных значений случайной величины вокруг ее среднего значения кроме дисперсии служат и некоторые другие характеристики. К их числу относится среднее квадратическое отклонение.

Средним квадратическим отклонением случайной величины X называют квадратный корень из дисперсии:

.

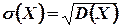Легко показать, что дисперсия имеет размерность, равную квадрату размерности случайной величины. Так как среднее квадратическое отклонение равно квадратному корню из дисперсии, то размерность s(Х) совпадает с размерностью X. Поэтому в тех случаях, когда желательно, чтобы оценка рассеяния имела размерность случайной величины, вычисляют среднее квадратическое отклонение, а не дисперсию.

Среднее квадратическое отклонение суммы

Взаимно независимых случайных величин

Теорема. Среднее квадратическое отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин:

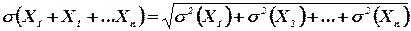или

.

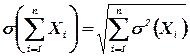Одинаково распределенные взаимно

Независимые случайные величины

Уже известно, что по закону распределения можно найти числовые характеристики случайной величины. Отсюда следует, что если несколько случайных величин имеют одинаковые распределения, то их числовые характеристики одинаковы.

Рассмотрим п взаимно независимых случайных величин Х₁, Х₂, … Х_n, которые имеют одинаковые распределения, а следовательно, и одинаковые характеристики. Обозначим среднее арифметическое рассматриваемых случайных величин через :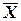

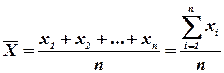
Имеют место следующие утвержденичя

1. Математическое ожидание среднего арифметического одинаково распределенных взаимно независимых случайных величин равно математическому ожиданию а каждой из величин:

.

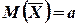2. Дисперсия среднего арифметического п одинаково распределенных взаимно независимых случайных величин п раз меньше дисперсии D каждой из величин:

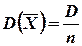
3. Среднее квадратическое отклонение среднего арифметического п одинаково распределенных взаимно независимых случайных величин в 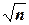раз меньше среднего квадратического отклонения s каждой из величин:

.

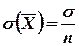ЗАКОН БОЛЬШИХ ЧИСЕЛ

Предварительные замечания

Оказывается, что при некоторых сравнительно широких условиях суммарное поведение достаточно большого числа случайных величин почти утрачивает случайный характер и становится закономерным. Эти условия и указываются в теоремах, носящих общее название закона больших чисел.

Теорема Чебышева

Теорема Чебышева. Если X_l, Х₂, ..., Х_n, X- попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышают постоянного числа С), то, как бы мало ни было положительное число e, вероятность неравенства

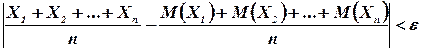
будет как угодно близка к единице, если число случайных величин достаточно велико.

Другими словами, в условиях теоремы

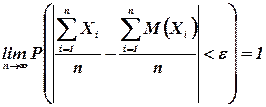
Таким образом, теорема Чебышева утверждает, что если рассматривается достаточно большое число независимых случайных величин, имеющих ограниченные дисперсии, то почти достоверным можно считать событие, состоящее в том, что отклонение среднего арифметического случайных величин от среднего арифметического их математических ожиданий будет по абсолютной величине сколь угодно малым.

Выше, формулируя теорему Чебышева, мы предполагали, что случайные величины имеют различные математические ожидания. На практике часто бывает, что случайные величины имеют одно и то же математическое ожидание. Очевидно, что если вновь допустить, что дисперсии этих величин ограничены, то к ним будет применима теорема Чебышева. Обозначим математическое ожидание каждой из случайных величин через а; в рассматриваемом случае среднее арифметическое математических ожиданий, как легко видеть, также равно а. Мы можем сформулировать теорему Чебышева для рассматриваемого частного случая.

Если X_l, Х₂, ..., Х_n - попарно независимые случайные величины, имеющие одно и то же математическое ожидание а, и если дисперсии этих величин равномерно ограничены, то, как бы мало ни было число e > 0, вероятность неравенства

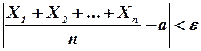
будет как угодно близка к единице, если число случайных величин достаточно велико.

Другими словами, в условиях теоремы будет иметь место равенство

Теорема Бернулли

Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А равна р. Можно ли предвидеть, какова примерно будет относительная частота появлений события? Положительный ответ на этот вопрос дает теорема, доказанная Якобом Бернулли (опубликована в 1713 г.), которая получила название «закона больших чисел» и положила начало теории вероятностей как науке. Доказательство Бернулли было сложным; простое доказательство дано П. Л. Чебышевым в 1846 г.

Теорема Бернулли. Если в каждом из п независимых испытаний вероятность р появления события А постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности р по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико: