ГЛАВА 9. Численные эксперименты в гидрологии

ГЛАВА 9. Численные эксперименты в гидрологии

Методы экспериментальных исследовании в геоэкологии

На первых странницах учебника отмечалось, что до недавнего времени [см. главу 1] в естественных науках, использовались почти исключительно два метода экспериментальных исследований: метод пассивного и метод активного эксперимента. В последние годы широкое распространение получил метод численных экспериментов.

Среди различных направлений использования численных экспериментов в исследовании природных процессов наибольшее распространение получил метод статистических испытаний или метод Монте-Карло. Это объясняется универсальностью метода. Действительно, численные эксперименты методом статистических испытаний позволяют:

— дать глубокий анализ процессов, на протекание которых влияют случайные факторы;

— решать многие математические задачи, не связанные с какими-либо случайностями. Например, сложные интегралы сейчас берутся, как правило, методом Монте-Карло.

Применение этого метода в практических расчетах заключается, например, во всестороннем анализе будущего режима работы проектируемых сложных систем, невозможном при использовании только календарного ряда наблюдений (продолжительность и вероятность циклов водности, возможные экстремальные значения стока на будущий период ограниченной продолжительности, что определяет объем водохранилища и режим их работы и т. д.).

В научной работе метод Монте-Карло используется для оценки различных методов анализа цикличности и расчетов стока, для решения вопроса о точности тех или иных статистических характеристик по выборкам для построения математических моделей и т. д.

В геоэкологии метод статистических испытаний используется как в практических расчетах, так и в научных исследованиях пока явно недо- статочно.

Поэтому в данном случае основное внимание будет уделено простейшим вопросам моделирования рядов наблюдений.. Вопросы применения этих моделей рассматриваются в соответствующих курсах.

Общее представление о методе Монте-Карло

9.2.1. Происхождение метода

Под методом Монте-Карло обычно понимается совокупность приемов, позволяющих получать решения различных задач с помощью многократных случайных испытаний.

Название метода происходит от города в княжестве Монако, знаменитого своим игорным домом. Это объясняется тем, что необходимым элементом метода Монте-Карло является последовательность случайных чисел, а одним из простейших механических приборов для получения этой последовательности является рулетка.

Подсознательно человечество использовало идеи метода Монте-Карло с незапамятных времен, когда на основании тех или иных экспериментов (как в области азартных игр, так и в области естественных наук) с последовательностью случайных явлений делались выводы о вероятности тех или иных значений. Первые по­пытки использовать построения, по смыслу аналогичные методу Монте-Карло, в гидрологии и водохозяйственных расчетах относятся к 1927 г. Они были сделаны в работе С. Садлера / /. В 1946 г. С. Н. Крицкий и М. Ф. Менкель на этой же основе смоделировали годовой ход уровня Каспийского моря / /. Однако годом рождения метода Монте-Карло считается 1949 г., когда появилась статья Метрополиса и Улама, в которой была сформулирована принципиальная сущность метода. В Советском Союзе первые данные о методе Монте-Карло были опубликованы в 1955—1956 гг. (В. В. Чавчавадзе, Ю. А. Шрейдер, В. С. Владимиров). Некоторое отставание начала исследований в нашей стране объяснялось общим отставанием в развитии ЭВМ, а развитие метода Монте-Карло как универсального численного метода стало возможным только благодаря появлению ЭВМ.

Впервые в применении к наукам о Земле методические основы применения метода Монте-Карло в достаточно полном виде были разработаны Г. Г. Сванидзе [ ]. С появлением первых работ Г. Г. Сванидзе значимость и число исследований с использованием этого метода непре­рывно стали возрастать.

Моделирование гидрологического ряда

По схеме случайной величины

Алгоритм счета и программа моделирования случайного ряда по схеме случайной величины чрезвычайно просты и во многом согласуются со схемой розыгрыша дискретной случайной величины (см. разд. 9.2.3). Так, пусть закон распределения моделируемого ряда задан в виде таблицы значений кривой обеспеченности Пирсона III типа .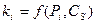

Статистические характеристики т_х, C_v и соотношение C_s/C_v моделируемого ряда известны. Тогда алгоритм моделирования по заданному ряду состоит в следующих операциях (рис. 9.4):

Вставить рис. 9.4 из числ. Методов, стр227

Рис. 9.4. Блок-схема моделирования по схеме случайной величины.

1) определение последовательности a_i (i= 1, 2, . .., N) (см. разд. 5.4);

2) перевод значений а_i в значения обеспеченности Р_i. Если в таблице обеспеченность задана в долях единицы, то Р_i=а_i, если в процентах, то P_i= 100а_i;

3) по известным P_i, С_s, C_v с таблицы 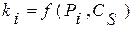считывается значение k_i, которое затем пересчитывается в х_i.

Эти операции повторяются N раз по заданному объему модели. Изложенный алгоритм моделирования по схеме случайного ряда достаточно легко ставится на ЭВМ.

Маркова

В результате моделирования по схеме простой цепи Маркова должен быть получен ряд X заданной продолжительности, закон распределения которого (одномерная 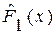и двухмерная F₂(x) функция распределения) и числовые характеристики 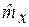, , 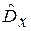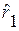при увеличении числа членов ряда стремятся к заданным законам распределения F₁(x), F₂(x) и числовым характеристикам т_х, D_x, .

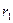В настоящее время существует почти три десятка различных способов моделирования по схеме простой цепи Маркова. Обзор, обоснование и систематизация этих способов дастся в работе Г. Г. Сванидзе [48].

В основном способы моделирования основаны на разложении членов ряда X на две составляющие

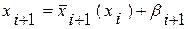(9.7)

или в модульных коэффициентах,

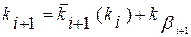, (9.8)

где 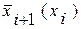и 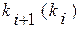—средние из возможных значений x_i+1 при данном x_i или k_i+1 при данном k_i , рассчитанные по уравнению регрессии x_i+1 по x_i, или k_i+1 по k_i (см. разд. 7.2); 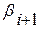и 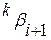случайные составляющие соответственно в исходных зна­чениях или в модульных коэффициентах, не зависящие от предшествующих значений исследуемого ряда.

Выше отмечалось, что характеристики разложений (9.7) или (9.8) задаются на основе тех или иных соображений или рассчитываются по какому-либо исходному ряду наблюдений. В последнем случае возникают серьезные затруднения, связанные с тем, что объем имеющихся выборочных данных наблюдений недоста­точен для точного определения параметров разложений.

Так, при имеющихся объемах выборок, практически невозможно установить истинную двухмерную функцию распределения F₂(x), определяющую закон распределения x_i+1(x_i) и β_i+1. Действительно, из анализа корреляционного поля k_i+1= f(k_i)_, (рис. 9.5) следует, что при малой тесноте связи, естественной, например, для рядов среднего годового и, тем более, максимального стока, выбор ка­кой-нибудь поверхности плотности вероятности практически не­возможен. В связи с этим остается неизвестной и форма связи k_i+1= f(k_i).

Вставить рис. 9.5

Рис. 9.5. График зависимости k_{i + y} = f(k,) среднего годового стока р. Волги у г. Старица. I, II, III — номера диапазона.

Единственный выход из создавшейся ситуации заключается в подборе подходящих гипотез о законе распределения и форме связи:

1) двухмерное распределение коррелированных величин k_i+1k_i, одномерные функции распределения которых являются гамма-распределением, также являются гамма-распределением;

2) зависимость k_i+1= f(k_i) определяется с помощью линейного уравнения регрессии.

Принимаемые гипотезы о законе распределения и форме связи, как отмечает Г. Г. Сванидзе, не могут быть непосредственно проверены на имеющемся статистическом материале. «Однако здесь на помощь приходит замечательное свойство метода Монте-Карло — возможность самопроверки»[1] [48].

При определении уравнения регрессии k_i+1 no k_i следует иметь в виду, что аппарат корреляции двух переменных величин разработан для случая, когда их закон распределения является нормальным, Для асимметричных законов распределения этот аппарат не всегда является достаточно эффективным. Поэтому в последнее время началась разработка аппарата гамма-корреляции для случая связи случайных величин, подчиняющихся гамма-распределению. Имеются также предложения об использовании гамма-корреляции при моделировании рядов стока по схеме простой цепи Маркова.

ГЛАВА 9. Численные эксперименты в гидрологии