Определение положения свободной поверхности

На произвольной поверхности равного давления Р → const, поэтому

дифференциал давления dp=0.Дифференциальное уравнение поверхности

X*dх+У*dy+Z*dz = 0, (4.15),

подставляем проекции (4.9,4.10,4.11) ускорения в (4.15)

-[aCosαdx+(αSina+g)dz]=0.(14.16)

После интегрирования

- [aCosα*x+ (aSinα + g)*z] +С₁ = 0. (4.17)

Изменяя начальные условия - С₁, получаем в жидкости поверхности равного давления параллельные свободной поверхности (изобарические).

Семейство поверхностей параллельно оси Y, одна из них - свободная поверхность.

Подставив начальные условия в формулу (4.17) х₀, z₀,находим для свободной поверхности

С₁ = aCosα x₀+ (aSinα + g)* z₀

Получаем уравнение свободной поверхности

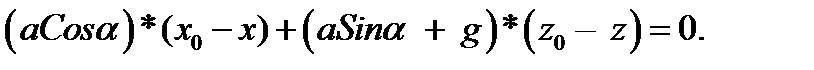
Связав в этом уравнении координаты z и x, получим уравнение прямой линии, как проекции свободной поверхности на вертикальную плоскость, β – угол наклона этой линии к оси х, связанной с сосудом

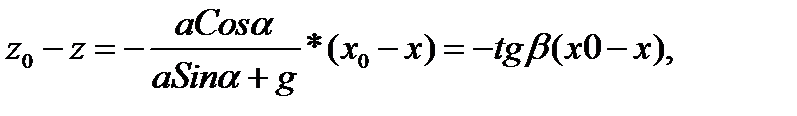(4.18)

,

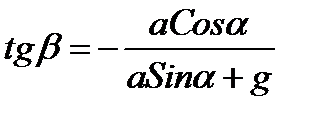где tgβ - тангенс угла наклона пьезометрической поверхности к оси Х.

Для определения положения свободной поверхности жидкости в сосуде, движущемся прямолинейно и равноускорено к уравнению (4.18) нужно добавить уравнение объемов, т. е. нужно знать первоначальный объем жидкости в сосуде и выразить его через размеры сосуда В и уровень Н жидкости в нем. Используя величины В и Н найдем Хо, Уо.

Некоторые случаи прямолинейного ускоренного движения.

Сосуд (рис.4.2а) движется по горизонтальной плоскости с постоянным ускорением а. Рассматривая равновесие частицы, находящейся на оси симметрии и поверхности жидкости, построим план ускорений, приложенных к частице.

Треугольник плана ускорений и треугольник с катетами ΔН и В/2 – подобны.

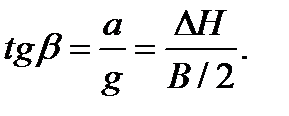
Положение свободной поверхности определиться углом β.

Если сосуд движется по наклонной плоскости (рис. 4.2б) под действием только силы тяжести, проектируем ускорение свободного падения g на ось параллельную плоскости - gSinα (с минусом, так как заданная ось Х направлена в противоположную сторону) и на горизонтальную ось Х.

Проекции ускорений на оси zOx

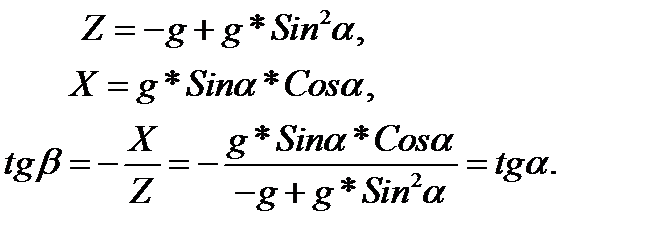
получим уравнение свободной поверхности в координатах zOx, и при отсутствии трения, получим угол β=α, тогда свободная поверхность горизонтальна.

Если сосуд движется вниз вертикально (рис.4.2в), j=-a, q=a-g, если сосуд движется вверх (рис.4.2г) q=a+g.

Можно также использовать суммарную массовую единичную силу q для определения давления в любой точке.

.

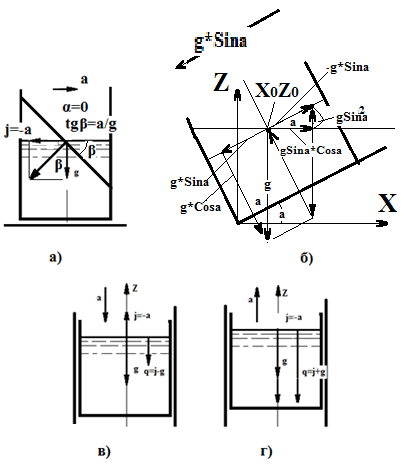
Рис.4.2.Движение сосуда по наклонной плоскости по горизонтальной плоскости (а), под действием собственного веса (б), вниз с ускорением(в), вверх с ускорением(г).

Возьмем на рис.4.1 около точки М площадку dS, параллельную свободной поверхности, и на этой площадке построим цилиндрический объем с осью, нормальной к свободной поверхности. Условие равновесия указанного объема жидкости в направлении нормали к свободной поверхности будет иметь вид

РdS = P₀dS + q(ρl_MdS),

где последний член представляет собой полную массовую силу, q – суммарная единичная массовая сила, М = ρl_MdS - масса выделенного объема жидкости, l— расстояние от точки М до свободной поверхности. После сокращения на dS получим давление в точке

Р = P₀ + qρl_M, (4.19)