Проверка прочности по различным теориям

Вычисление главных и эквивалентных напряжений в стержневых, плоскостных и объемных конечных элементах по усилиям от отдельных загружений, а также по расчетным сочетаниям загружений (РСН) или по РСУ производится при помощи системы ЛИТЕРА.

Главные напряжения

Главные напряжения вычисляются в соответствии с видом напряженно-деформированного состояния (НДС), полученного в результате расчета схемы. Каждый тип конечных элементов обладает определенными особенностями, соответствующими тому НДС, которое ими моделируется при создании расчетной схемы. Так, например, КЭ балки-стенки моделируют плоское напряженное состояние и т.п.

В общем случае НДС в точке тела описывается шестью осевыми компонентами тензора напряжений:

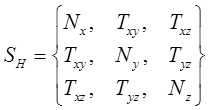(12.1)

Возможны случаи, когда какие-либо напряжения равны нулю. Для плоского НДС, например, тензор напряжений принимает вид:

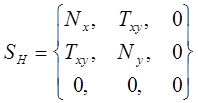(12.2)

В любом случае главные напряжения выстраиваются так: N1³N2³N3.

КЭ плоской задачи теории упругости

Моделируется плоское напряженное состояние в плоскости X1OZ1.

Главные напряжения вычисляются в центре тяжести каждого элемента в его срединной поверхности:

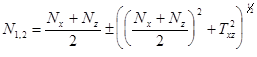(12.3)

Угол наклона наибольшего главного напряжения N1 к оси X1:

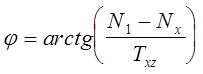(12.4)

КЭ плиты

Моделируется напряженное состояние в плоскости X1OY1, характеризуемое изгибными усилиями. Осевые напряжения вычисляются для нижней и верхней поверхностей:

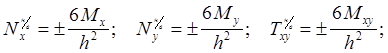(12.5)

h-толщина плиты.

Главные напряжения и углы их наклона вычисляются по формулам (12.3) и (12.4).

В срединной поверхности возникают касательные напряжения:

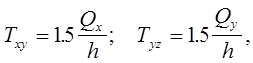(12.6)

которые при вычислении главных напряжений игнорируются.

КЭ объемного НДС

Определение главных напряжений в этом случае производится из решения кубического уравнения.

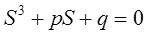(12.7)

где :

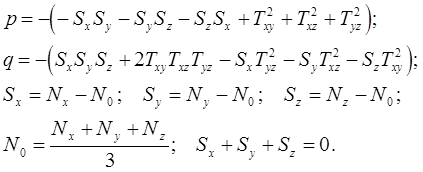
Корни уравнения (12.7):

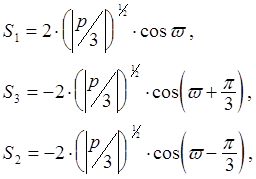(12.8)

где :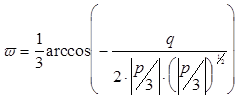

Главные напряжения:

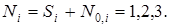(12.9)

Затем вычисляются направляющие косинусы углов наклона осей к осям местной системы координат КЭ из системы уравнений вида:

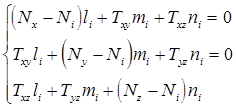(12.10)

где i=1,2,3.

Решив систему трижды, получим матрицу направляющих косинусов:

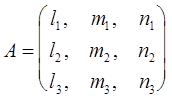(12.11)

В этом случае вычисляются три угла Эйлера, определяющие положение трех главных напряжений относительно местной системы координат (рис. 12.1):

- q (тета)- угол (нутации) между положительными направлениями осей OZ1 и N3 (0 £ q £ p);

- y (пси) - угол (прецессии) между осью OX1 и осью OA (линия пересечения плоскостей X1OY1 и N1ON2), положительное направление которой выбирается так, что OA, OZ1 и N3 образуют правую тройку. Угол y отсчитывается от оси OX1 к OY1 (0 £ y £ 2p)

- j - (фи) - угол (чистого вращения) между осями N1 и ОA отсчитывается от оси N1 к N2 (0 £ j £ 2p).

Значения углов Эйлера определяются так:

q = arccos (n₃) (12.12)

При q = 0, j = 0, y = arcsin (m₁),

причем если l₁ < 0, то y = p-arcsin (m₁).

Если y < 0, то y =y +2p . (12.13)

При q ¹ 0 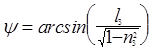, причем если ,

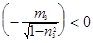то

Если y < 0, то y =y +2p . (12.14)

Далее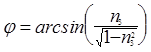

причем если ,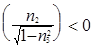

то .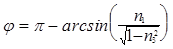

Если j < 0, то j = j +2p .

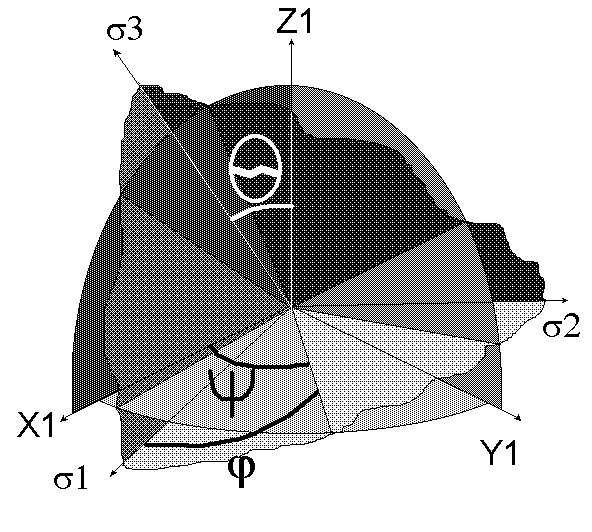
Рис. 12.1

КЭ оболочки

Моделируется напряженное состояние (в плоскости X1OY1), характеризуемое нормальными и касательными напряжениями в срединной поверхности, а также изгибными усилиями.

Осевые напряжения вычисляются для нижней и верхней поверхностей:

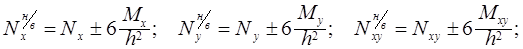(12.15)

Главные напряжения для этих поверхностей вычисляются по формулам (12.3) и (12.4).

В срединной поверхности игнорируется влияние напряжений T_xy, T_yz от перерезывающих сил.

Вид НДС

Для объемных конечных элементов производится вычисление параметра Лоде-Надаи, характеризующего вид НДС.

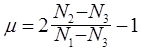(12.16)

Значение

m = 1 - характеризует чистое сжатие;

m = 0 - чистый сдвиг;

m = -1 - чистое растяжение.

Стержневые КЭ

Главные напряжения в сечениях стержней вычисляются по формуле:

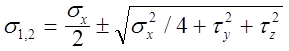(12.17)

где s_x , t_y , t_z нормальное и касательные напряжения в характерных точках сечения стержня.

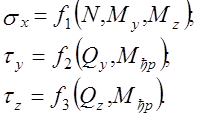(12.18)

В табл. 12.1 приведены характерные точки для реализованных типов сечений стержней.

Для сечений, не указанных в табл. 12.1, а также для сечений, заданных при помощи численных жесткостей и из базы профилей стального проката, главные и эквивалентные напряжения могут быть вычислены с помощью системы ЛИР-КС.

Для нестандартных сечений главные и эквивалентные напряжения вычисляются только с помощью системы ЛИР-КС.

Таблица 12.1.

Тип сече-ния	Форма сечения	Примечание
S0		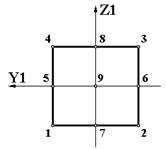1. Всего 9 точек.
S1		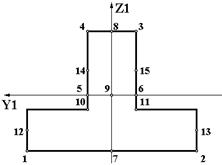1. Точки 5 и 6 всегда лежат на пересечении оси Y1 с контуром сечения. 2. Точки 10 и 11 принадлежат стенке тавра у стыка с полкой. 3. Точки 12 и 13 расположены посредине высоты полки. 4. Точки 14 и 15 расположены посредине высоты стенки. 5. Всего 15 точек.
S2		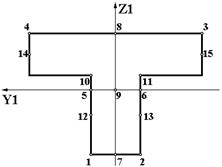1. Точки 5 и 6 всегда лежат на пересечении оси Y1 с контуром сечения. 2. Точки 10 и 11 принадлежат стенке тавра у стыка с полкой. 3. Точки 12 и 13 расположены посредине высоты стенки. 4. Точки 14 и 15 расположены посредине высоты полки. 5. Всего 15 точек.
S3		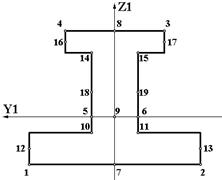1. Точки 5 и 6 всегда лежат на пересечении оси Y1 с контуром сечения. 2.Точки 10 и 11, 14 и 15 принадлежат стенке в месте стыка с нижней и верхней полками. 3.Точки 12 и 13, 16 и 17 находятся на серединах высот нижней и верхней полок. 4. Точки 18 и 19 расположены посредине высоты стенки. 5. Всего 19 точек.
S4		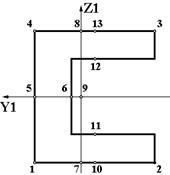1. Точки 5 и 6 всегда лежат на пересечении оси Y1 с контуром сечения. 2. Точки 7 и 8 всегда лежат на пересечении оси Z1 с контуром сечения. 3. Точки 10, 11, 12, 13 лежат на одной вертикали, проходящей через середину полок. 4. Точки 14 и 15 принадлежат стенке у стыков с полками. 5. Всего 15 точек.
S5		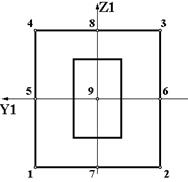1. Всего 9 точек.
S6		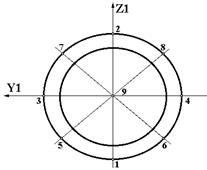1. Всего 9 точек. 2. При вычислении напряжений в точках 5-8 учитывается толщина кольца.
S7		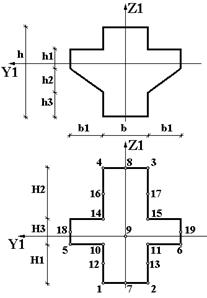1. Сечение приводится к кресту: 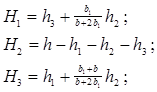2. Центр тяжести вычисляется для реального сечения. 3. Точки 5 и 6 всегда лежат на пересечении оси Y1 с контуром крестового сечения. 4. Точки 10, 11, 14, 15 принадлежат стенке у стыка с поперечиной. 5. Точки 12, 13, 16 и 17 лежат на серединах высот H1 и H2. 6. Точки 18 и 19 расположены посредине высоты H3. 7. Всего 19 точек.