Решение систем линейных уравнений.

1. Матричный метод.

Пусть имеется система 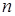– го порядка

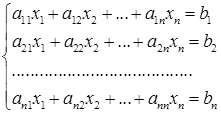
Матрица 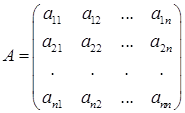– матрица системы;

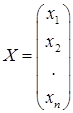– столбец неизвестных; 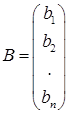– столбец свободных членов.

Данная система эквивалентна матричному уравнению: 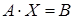, тогда решение системы эквивалентно решению указанного матричного уравнения т.е. .

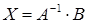2. Правило Крамера.

Если определитель 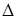системы 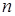линейных уравнений с 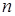неизвестными отличен от нуля, то эта система имеет единственное решение, которое может быть найдено по формулам

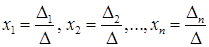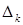, где – определитель, полученный из главного заменой 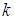– го столбца столбцом свободных членов.

Замечание: а) Если 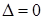, а какой-либо из 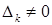, то, очевидно, что система решений не имеет.

б) Если все определители одновременно равны нулю, то система либо имеет бесчисленное множество решений, либо несовместна.

3. Метод Гаусса (метод исключения неизвестных).

Пусть дана произвольная система линейных уравнений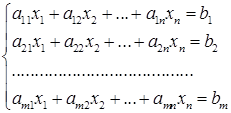

Расширенной матрицей системы назовем матрицу полученную из А добавлением столбца свободных членов .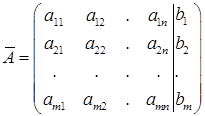

Под элементарными преобразованиями системы линейных уравнений понимаются следующие операции:

1. Умножение какого-либо уравнения системы на число, отличное от нуля;

2. Прибавление к одному уравнению другого уравнения, умноженного на произвольное число;

3. Перемена местами двух уравнений в системе.

Очевидно, что каждому элементарному преобразованию системы соответствует аналогичное преобразование строк расширенной матрицы этой системы и наоборот.

Элементарные преобразования системы обратимы, т.е. если мы, сделав элементарное преобразование, перешли от одной системы к другой, то можем вернуться к первоначальной, выполнив некоторое другое преобразование.

Определение: две системы линейных уравнений от одних и тех же переменных называются равносильными, если каждое решение одной из них является решением другой, и наоборот (или лбе системы несовместны).

При элементарных преобразованиях система переходит в равносильную систему.

Метод Гаусса заключается в том, что при помощи элементарных преобразований систему (расширенную матрицу) приводят к трапециевидной форме. После этого уже не представляет труда разобраться в вопросе о совместности системы, определить число решений и найти сами решения.

Векторы и действия с ними.

Вектором назовем направленный отрезок в пространстве. Обозначения: 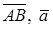. Длина отрезка AB является длиной вектора . Нулевой вектор – вектор имеющий нулевую длину.

Векторы коллинеарны, если они лежат на одной прямой или на параллельных прямых. Векторы компланарны, если они лежат в одной плоскости, или в параллельных плоскостях.

Два вектора называются равными, если они

a) коллинеарны,

b) одинаково направлены,

c) имеют равные длины.

Из определения следует, что вектор можно переносить параллельно самому себе в любую точку пространства. Такой вектор называется свободным.

Пусть даны два вектора 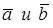. Построим равные им векторы 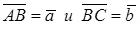. Тогда вектор 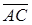называется суммой векторов . .

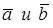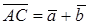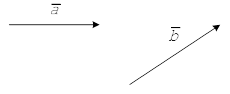
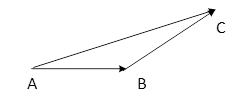
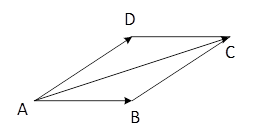
Этот способ называется «правило треугольника». Векторы можно складывать и по «правилу параллелограмма» (см рис.)

Разностью двух векторов 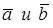называется сумма векторов 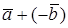. Вычитание действие обратное сложению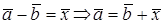

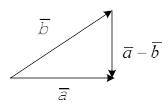
Произведение вектора 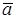на число 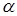называется вектор :

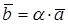а)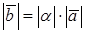

б) 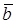коллинеарен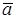

в) 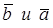одинаково направлены, если 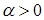и противоположно направлены, если .

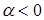Выражение 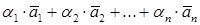называется линейной комбинацией векторов.

Базисом в пространстве называются три любых не компланарных вектора, взятые в определенном порядке.

Базисом на плоскости называются два любых не коллинеарных вектора, взятых в определенном порядке.

Если 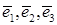- базис в пространстве, то коэффициенты разложения вектора 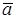по базису 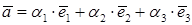называются координатами

Каждый вектор в плоскости может быть единственным образом разложен по данному базису этой плоскости;

Каждый вектор пространства может быть единственным образом разложен по данному базису в пространстве.

Равные векторы имеют равные координаты.

При умножении вектора на число все его координаты умножаются на это число.

При сложении векторов складываются их координаты.

Прямоугольная декартова система координат.

Прямоугольной декартовой системой координат в пространстве называется точка и базис, векторы которого

а) попарно перпендикулярны (ортогональны),

б) .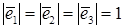

Точка называется началом координат. Прямые, проходящие через начало координат в направлении базисных векторов, называются осями координат (абсцисса, ордината, аппликата).

Приняты обозначения: .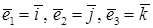

Координаты радиус-вектора точки M называются координатами точки M в данной системе координат.

Нетрудно проверить, что координаты точки в декартовой прямоугольной системе координат по абсолютной величине равны расстоянию от этой точки до координатных плоскостей. Они имеют знак (+) или (–) в зависимости от того в каком квадранте пространства она находится.

Пусть в данной прямоугольной декартовой системе координат вектор 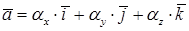. Найти длину вектора можно по формуле

.

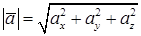Для того чтобы найти координаты вектора нужно из координат конца вычесть координаты начала.

Пусть даны точк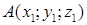и и 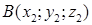, тогда координаты вектора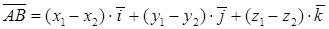

Пусть даны концы отрезка точки 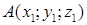, 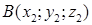и точка 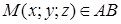и делящая его в отношении 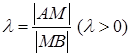. Тогда координаты точки 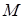вычисляются по формулам ; ; .

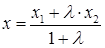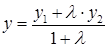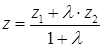Следствие: Координаты середины отрезка равны среднему арифметическому координат концов отрезка.

; ; .

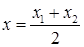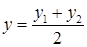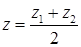Пусть в данной прямоугольной декартовой системе координат даны векторы

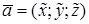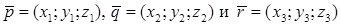, , причем векторы 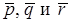сами образуют базис. Вектор 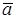можно разложить по базису 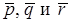т.е. записать в виде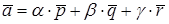

.

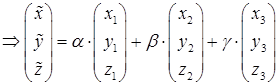Таким образом, решение задачи сводится к решению системы линейных уравнений

.
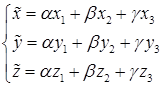