Симплекс-метод с естественным базисом

Для применения этого метода задача линейного программирования должна быть сформулирована в канонической форме, причем матрица системы уравнений должна содержать единичную подматрицу размерностью . В этом случае очевиден начальный опорный план (неотрицательное базисное решение).

Для определенности предположим, что первые т векторов матрицы системы составляют единичную матрицу. Тогда очевиден первоначальный опорный план: .

Проверка на оптимальность опорного плана проходит с помощью критерия оптимальности, переход к другому опорному плану — с помощью преобразований Жордана-Гаусса и с использованием критерия оптимальности.

Полученный опорный план снова проверяется на оптимальность и т.д. Процесс заканчивается за конечное число шагов, причем на последнем шаге либо выявляется неразрешимость задачи (конечного оптимума нет), либо получаются оптимальный опорный план и соответствующее ему оптимальное значение целевой функции.

Признак оптимальности заключается в следующих двух теоремах.

Теорема 1. Если для некоторого вектора, не входящего в базис, выполняется условие:

, где ,

то можно получить новый опорный план, для которого значение целевой функции будет больше исходного; при этом могут быть два случая:

1. если все координаты вектора, подлежащего вводу в базис, неположительны, то задача линейного программирования не имеет решения;

2. если имеется хотя бы одна положительная координата у вектора, подлежащего вводу в базис, то можно получить новый опорный план.

Теорема 2. Если для всех векторов выполняется условие , то полученный план является оптимальным.

На основании признака оптимальности в базис вводится вектор ,давший минимальную отрицательную величину симплекс-разности: .

Чтобы выполнялось условие неотрицательности значений опорного плана, выводится из базиса вектор _г, который дает минимальное положительное отношение:

; , .

Строка называется направляющей, столбец и элемент
— направляющими(последний называют также разрешающимэлементом).

Элементы вводимой строки, соответствующей направляющей строке, в новой симплекс-таблице вычисляются по формулам:

,

а элементы любой другой 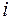-й строки пересчитываются по формулам:

, ,

Значения базисных переменных нового опорного плана (показатели графы «план») рассчитываются по формулам:

для ; , для .

Если наименьшее значение 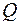достигается для нескольких базисных векторов, то чтобы исключить возможность зацикливания (повторения базиса), можно применить следующий способ.

Вычисляются частные, полученные от деления всех элементов строк, давших одинаковое минимальное значение 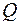на свои направляющие элементы. Полученные частные сопоставляются по столбцам слева направо, при этом учитываются и нулевые, и отрицательные значения. В процессе просмотра отбрасываются строки, в которых имеются большие отношения, и из базиса выводится вектор, соответствующий строке, в которой раньше обнаружится меньшее частное.

Для использования приведенной выше процедуры симплекс-метода к минимизации линейной формы следует искать максимум функции , затем полученный максимум взять с противоположным знаком. Это и будет искомый минимум исходной задачи линейного программирования.

Симплексный метод с искусственным базисом (М-метод)

Симплексный метод с искусственным базисом применяется в тех случаях, когда затруднительно найти первоначальный опорный план исходной задачи линейного программирования, записанной в канонической форме.

М-метод заключается в применении правил симплекс-метода к так называемой М-задаче. Она получается из исходной добавлением к левой части системы уравнений в канонической форме исходной задачи линейного программирования таких искусственных единичных векторов с соответствующими неотрицательными искусственными переменными, чтобы вновь полученная матрица содержала систему единичных линейно-независимых векторов. В линейную форму исходной задачи добавляется в случае её максимизации слагаемое, представляющее собой произведение числа (–М) на сумму искусственных переменных, где М – достаточно большое положительное число.

В полученной задаче первоначальный опорный план очевиден. При применении к этой задаче симплекс-метода оценки теперь будут зависеть от числа М. Для сравнения оценок нужно помнить, что М – достаточно большое положительное число, поэтому из базиса будут выводиться в первую очередь искусственные переменные.

В процессе решения М–задачи следует вычеркивать в симплекс-таблице искусственные векторы по мере их выхода из базиса. Если все искусственные векторы вышли из базиса, то получаем исходную задачу. Если оптимальное решение М–задачи содержит искусственные векторы или М–задача неразрешима, то исходная задача также неразрешима.

Путем преобразований число вводимых переменных, составляющих искусственный базис, может быть уменьшено до одной.

Теория двойственности

Любой задаче линейного программирования можно сопоставить сопряженную или двойственную ей задачу. Причем, совместное исследование этих задач дает, как правило, значительно больше информации, чем исследование каждой из них в отдельности.

Любую задачу линейного программирования можно записать в виде:

Первоначальная задача называется исходной или прямой.

Модель двойственной задачи имеет вид:

Переменные двойственной задачи 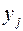называют объективно обусловленными оценками или двойственными оценками.

Связь исходной и двойственной задач заключается, в частности, в том, что решение одной из них может быть получено непосредственно из решения другой. Каждая из задач двойственной пары фактически является самостоятельной задачей линейного программирования и может быть решена независимо от другой.

Двойственная задача по отношению к исходной составляется согласно следующим правилам:

1.целевая функция исходной задачи формулируется на максимум, а целевая функция двойственной задачи – на минимум, при этом в задаче на максимум все неравенства в функциональных ограничениях имеют вид , а в задаче на минимум – вид ;

2.матрица составленная из коэффициентов при неизвестных в системе ограничений исходной задачи, и аналогичная матрица в двойственной задаче получаются друг из друга транспонированием;

3.Число переменных в двойственной задаче равно числу функциональных ограничений исходной задачи, а число ограничений в системе двойственной задачи – числу переменных в исходной задаче;

4.Коэффициентами при неизвестных в целевой функции двойственной задачи являются свободные члены в системе ограничений исходной задачи, а правыми частями в ограничениях двойственной задачи – коэффициенты при неизвестных в целевой функции исходной задачи;

5.Каждому ограничению одной задачи соответствует переменная другой задачи: номер переменной совпадает с номером ограничения; при этом ограничению, записанному в виде неравенства , соответствует переменная, связанная условием неотрицательности. Если функциональное ограничение исходной задачи является равенством, то соответствующая переменная двойственной задачи может принимать как положительные, так и отрицательные значения.

Математические модели пары двойственных задач могут быть симметричными и несимметричными. В несимметричных двойственных задачах система ограничений исходной задачи задается в виде равенств, а двойственной – в виде неравенств, причем переменные в двойственной задаче могут быть и отрицательными. В симметричных двойственных задачах система ограничений как исходной, так и двойственной задачи задается в виде неравенств, причем на двойственные переменные налагается условие неотрицательности.

Исходная задача	Двойственная задача
Симметричные пары
Несимметричные пары

где:

, .

,

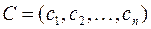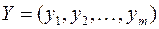
Рассмотрим пример, показывающий, как в реальной экономической ситуации появляются взаимно двойственные задачи линейного программирования.

На некотором предприятии после выполнения годового плана возник вопрос: как поступить с остатками сырья? Из оставшегося сырья можно наладить производство продукции и реализовать его или продать сырье.

Предположим, что имеется два вида сырья и , остатки которого составляют соответственно 35 и 20 единиц. Из этого сырья можно наладить производство трех видов товаров: , и .

Виды товаров			Прибыль
Запасы

При исследовании первой возможности (наладить выпуск товаров , и ) возникает вопрос о плане выпуска, который задается тремя переменным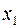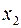и , и , которые соответствуют количеству произведенного товара. Эти переменные должны удовлетворять условиям:

Прибыль, которую получит предприятие от реализации товара, составит:

В интересах предприятия эту прибыль максимизировать.

Это прямая задача.

Объективно обусловленными оценками двойственной задачи и будут цены, по которым целесообразно продавать излишки сырья, т.е. при продаже сырья по ценам ниже и предприятие будет терпеть убытки.

Справедливое требование со стороны продающего предприятия состоит в следующем: если взять сырье, идущее на производство единицы товара , то выручка от его продажи должна быть не меньше, чем прибыль от реализации готового изделия (в противном случае нет смысла продавать сырье – целесообразнее изготовить товар и получить прибыль от его реализации).

Это требование можно представить в виде системы неравенств:

В левой части каждого неравенства предполагаемая выручка от продажи сырья, необходимого для производства единицы товара , а в правой – прибыль от реализации этой единицы товара.

Что касается покупателя, то он заинтересован в минимизации расходов на покупку сырья, т.е. величины .

Теоремы двойственности

Теоремы двойственности позволяют установить взаимосвязь между оптимальными решениями пары двойственных задач: можно либо найти оптимальное решение другой задачи, не решая ее, либо установить его отсутствие.

Возможны следующие случаи:

· обе задачи из пары двойственных имеют оптимальные решения;

· одна из задач не имеет решения ввиду неограниченности целевой функции, а другая – ввиду несовместности системы ограничений.