Теорема о делении с остатком

Для любых многочленов существуют многочлены и , такие, что причем степень меньше степени или . Многочлены и определены однозначно.

Многочлены и называются соответственно частным и остатком. Если делит то остаток .

Число называется корнем многочлена , если .

Теорема Безу

Число является корнем многочлена тогда и только тогда, когда делится на

Пусть ‑ корень многочлена , т.е. Разделим на ,где степень меньше степени , которая равна Значит, степень равна 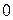, т.е. . Значит, , . Так как , то из последнего равенства следует, что т.е. .

Обратно, пусть делит , т.е. . Тогда .

Следствие.Остаток от деления многочлена на равен .

Многочлены первой степени называются линейными многочленами. Теорема Безу показывает, что разыскание корней многочлена равносильно разысканию его линейных делителей со старшим коэффициентом 1.

Многочлен можно разделить на линейный многочлен с помощью алгоритма деления с остатком, но существует более удобный способ деления, известный под названием схемы Горнера.

Пусть и пусть ,где . Сравнивая коэффициенты при одинаковых степенях неизвестной с левой и правой частях последнего равенства, имеем:

, откуда

(11.1)

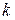Число называется корнем кратности многочлена , если делит , но уже не делит .

Чтобы поверить, будет ли число корнем многочлена и какой кратности, можно воспользоваться схемой Горнера. Сначала делится на затем, если остаток равен нулю, полученное частное делится на и т.д. до получения не нулевого остатка.

Число различных корней многочлена не превосходит его степени.

Большое значение имеет следующая основная теорема.

Основная теорема. Всякий многочлен с числовыми коэффициентами ненулевой степени имеет хотя бы один корень (может быть комплексный).

Следствие. Всякий многочлен степени имеет в C (множестве комплексный чисел) столько корней, какова его степень, считая каждый корень столько раз, какова его кратность.

(11.2)

где ‑ корни , т.е. во множестве C всякий многочлен разлагается в произведение линейных множителей. Если одинаковые множители собрать вместе, то:

,

где уже различные корни , ‑ кратность корня .

Если многочлен , , с действительными коэффициентами имеет корень , то число также корень

Значит, у многочлена с действительными коэффициентами комплексные корни входят парами.

Следствие. Многочлен с действительными коэффициентами нечетной степени имеет нечетное число действительных корней.

Пусть и корни Тогда делится на и но так как у и нет общих делителей, то делится на прозведение .

Утверждение 2. Многочлен с действительными коэффициентами степени всегда разлагается на множестве действительных чисел в произведение линейных многочленов, отвечающих его вещественным корням, и многочленов 2-ой степени, отвечающих паре сопряженных комплексных корней.

При вычислении интегралов от рациональных функций нам понадобится представление рациональной дроби в виде суммы простейших.

Рациональной дробью называется дробь где и ‑ многочлены с действительными коэффициентами, причем многочлен . Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя. Если рациональная дробь не является правильной, то, произведя деление числителя на знаменатель по правилу деления многочленов, ее можно представить в виде , где и – некоторые многочлены, а – правильная рациональная дробь.

Лемма 1. Если – правильная рациональная дробь, а число является вещественным корнем кратности многочлена , т.е. и , то существует вещественное число и многочлен с вещественными коэффициентами, такие, что где дробь также является правильной.

При этом несложно показать, что полученное выражение является рациональной дробью с вещественными коэффициентами.

Лемма 2. Если – правильная рациональная дробь, а число ( и – вещественные, ) является корнем кратности многочлена , т.е. и , и если , то существуют вещественные числа и и многочлен с вещественными коэффициентами, такие, что где дробь также является правильной.

Рациональные дроби вида , , , , ‑ трехчлен с действительными коэффициентами, не имеющий действительных корней, называются простейшими (или элементарными) дробями.

Всякая правильная рациональная дробь представима единственным образом в виде суммы простейших дробей.

При практическом получении такого разложения оказывается удобным так называемый метод неопределенных коэффициентов. Он состоит в следующем:

· Для данной дроби пишется разложение, в котором коэффициенты считаются неизвестными ;

· После этого обе части равенства приводятся к общему знаменателю и у получившихся в числителе многочленов приравниваются коэффициенты.

При этом если степень многочлена равна , то в числителе после приведения к общему знаменателю получается многочлен степени , т.е. многочлен с коэффициентами.

Число неизвестных также равняется : .

Таким образом, получается система уравнений с неизвестными. Существование решения у этой системы следует из приведенной выше теоремы.

Контрольные вопросы к лекции №11

1. Понятие многочлена.

2. Условие равенства многочленов.

3. Сложение и умножение многочленов.

4. Теорема о делении с остатком.

5. Понятие корня многочлена.

6. Понятие кратности корня многочлена

7. Теорема Безу.

8. Схема Горнера.

9. Соотношение степени многочлена и числа его корней.

10. Понятие правильной рациональной дроби.

11. Разложение правильной рациональной дроби на простейшие.

12. Метод неопределенных коэффициентов.