Плотность распределения, функция распределения и числовые характеристики непрерывной случайной величины (НВС). Нормальное распределение.
3.7.1. Плотность распределения вероятностей НСВ Х имеет вид:
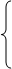

Сх2, если - 1 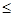 х
х 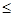 1,
1,
f (x)=
0, если |x|>1.
Найти: а) константу С; б) Р (Х 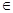 [-2;0]); в) M[Х]; г) D[Х]; д) функцию распределения F(x).
[-2;0]); в) M[Х]; г) D[Х]; д) функцию распределения F(x).
3.7.2. Плотность распределения вероятностей НСВ Х имеет вид:
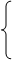
0, если х 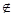 [0;
[0; 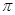 ],
],
f (x)=
Csin x, если х 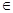 [0;
[0; 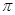 ].
].
Найти: а) константу С; б) Р (Х 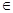 [
[ 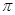 /3; 5
/3; 5 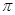 /4]); в) M[Х]; г) функцию распределения F(x).
/4]); в) M[Х]; г) функцию распределения F(x).
3.7.3. Плотность распределения вероятностей НСВ Х имеет вид:
 0, если x<5,
0, если x<5,
f (x)=
C/x5, если х 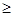 5.
5.
Найти: а) константу С; б) M[Х]; в) D[Х]; г) P(2<Х<10); д) функцию распределения F(x).
 3.7.4. Плотность распределения вероятностей НСВ Х имеет вид:
3.7.4. Плотность распределения вероятностей НСВ Х имеет вид:
0, если x<1,
f (x)=
C e-2x, если х 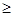 1.
1.
Найти: а) константу С; б) P (|X| 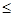 2); в) функцию распределения F(x).
2); в) функцию распределения F(x).
3.7.5. Функция распределения НСВ Х имеет вид:
 |
1) 0, если x<2,
F (x)= (x – 2)2, если 2 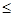 х
х 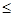 3
3
1, если x>3
2) 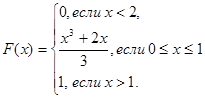
Найти: а) P (0,5 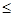 X
X 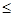 2,5); б) M[X]; в) D[X].
2,5); б) M[X]; в) D[X].
3.7.6. Функция распределения НСВ Х имеет вид:
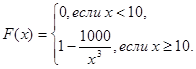
Найти: а) Р(5 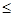 Х<15); б) M[X]; в) D[X].
Х<15); б) M[X]; в) D[X].
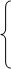 3.7.7. Функция распределения НСВ Х имеет вид:
3.7.7. Функция распределения НСВ Х имеет вид:
0, если x<0,
F (x)=
1 – e-3x, если х 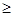 0
0
Найти а) плотность распределения f(x); б) Р(1 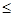 Х<2).
Х<2).
3.7.8. Автобусы идут с интервалом в 5 минут. Считая, что случайная величина Х – время ожидания автобуса на остановке – распределена равномерно на указанном интервале, найти среднее время ожидания и дисперсию времени ожидания.
3.7.9. Время ожидания у бензоколонки АЗС является случайной величиной Х, распределенной по показательному закону со средним временем ожидания, равным 6 минутам. Найти: а) Р(3 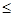 Х<9); б) Р (Х
Х<9); б) Р (Х 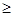 12).
12).
3.7.10. Случайная величина распределена по нормальному закону с параметрами m=3, 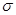 =5. Найти Р(-2
=5. Найти Р(-2 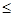 Х<13).
Х<13).
3.7.11. Случайная величина Х имеет нормальное распределение с параметрами m=1, 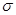 =2. Найти Р(3
=2. Найти Р(3 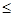 Х<7).
Х<7).
3.7.12. Плотность распределения случайной величины Х имеет вид:
1)
f (x)= 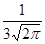 e
e 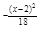
2)
f (x)= 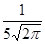 e
e 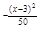
Найти M[X], D[X], P(-7 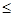 X<8).
X<8).
3.7.13. Длина детали, изготавливаемой на автоматическом станке, является случайной величиной, распределенной по нормальному закону с параметрами m=20, 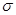 =0,2. Найти вероятность того, что длина детали будет находиться в интервале (19,7; 20,3). Какую точность изготовления можно гарантировать с вероятностью 0,9?
=0,2. Найти вероятность того, что длина детали будет находиться в интервале (19,7; 20,3). Какую точность изготовления можно гарантировать с вероятностью 0,9?
3.7.14. Производится измерение без систематических ошибок диаметра вала. Случайные ошибки измерения Х подчинены нормальному распределению со среднеквадратическим отклонением 10мм. Найти вероятность того, что измерение будет произведено с ошибкой, не превосходящей по абсолютной величине 15мм.
3.7.15. Производится взвешивание некоторого вещества без систематических ошибок. Случайные ошибки взвешивания подчинены нормальному закону со среднеквадратическим отклонением 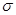 =20г. Найти вероятность того, что взвешивание будет произведено с ошибкой, не превосходящей по абсолютной величине 10г.
=20г. Найти вероятность того, что взвешивание будет произведено с ошибкой, не превосходящей по абсолютной величине 10г.
3.7.16. Весы работают с распределенной нормально ошибкой, имеющей среднее значение 10кг и среднеквадратическое отклонение 5кг. Найти вероятность того, что ошибка превысит 15кг.
3.7.17. Изделие, изготавливаемое автоматом, считается годным, если отклонение его контролируемого размера от проектного не превышает 10мм. Случайные отклонения контролируемого размера от проектного подчинены нормальному закону со среднеквадратическим отклонением 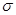 =5мм и средним m=0. Сколько процентов годных изделий в среднем изготавливает автомат?
=5мм и средним m=0. Сколько процентов годных изделий в среднем изготавливает автомат?
3.7.18. Завод изготавливает шарики для подшипников. Номинальный диаметр шариков d0=5мм. Фактический диаметр – случайная величина, распределенная по нормальному закону со средним d0 и среднеквадратическим отклонением 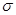 = 0,05мм. При контроле бракуются шарики, диаметр которых отличается от номинального больше, чем на 0,1мм. Определить, какой процент шариков будет в среднем отбраковываться.
= 0,05мм. При контроле бракуются шарики, диаметр которых отличается от номинального больше, чем на 0,1мм. Определить, какой процент шариков будет в среднем отбраковываться.
3.7.19.Измеряемая случайная величина Х имеет нормальное распределение с параметрами m=10, 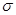 =5. Найти симметричный относительно m интервал, в который измеренное значение попадает с вероятностью: а) 0,9974; б) 0,9544; в) 0,5.
=5. Найти симметричный относительно m интервал, в который измеренное значение попадает с вероятностью: а) 0,9974; б) 0,9544; в) 0,5.
3.7.20. В условиях задачи 3.7.18найти симметричный относительно d0 интервал, в котором с вероятностью 0,9974 будут заключены диаметры изготавливаемых шариков.
3.7.21. В нормально распределенной совокупности 15% значений х меньше 12 и 40% значений х больше 16,2. Найти среднее значение и стандартное отклонение данного распределения.
3.7.22. Средняя масса выпекаемых в кондитерском цехе тортов «Прага» равна 1,06кг. Известно, что 5% тортов имеют массу, меньшую 1кг. Каков процент тортов, масса которых не менее 940г?
3.7.23. Масса батона является случайной величиной, распределенной по нормальному закону со средним 500г и среднеквадратическим отклонением 8г. Найти вероятность того, что из трех батонов два будут иметь массу меньше 490г.
3.7.24. Непрерывная случайная величина X имеет функцию распределения F(x)=0,5+(arctg x)/p. Для X найти функцию плотности вероятности f(x) и вероятность P(0<X<1). Обладает ли X математическим ожиданием?
3.7.25. Пусть X – непрерывная случайная величина, распределенная по нормальному закону с математическим ожиданием 20 и средним квадратическим отклонением 60. Найти вероятность того, что |X|<100.
3.7.26. Пусть X – непрерывная случайная величина, распределенная по показательному закону с параметром l. Для случая M(X) = 0,5 найти вероятность P(1<X<2).
3.7.27. Пусть X – непрерывная случайная величина, равномерно распределенная на отрезке [a,b]. Для X найти математическое ожидание M(X) и дисперсию D(X).
3.7.28. Поезда метро идут через данную станцию с интервалом две минуты. Пассажир приходит на станцию в случайный момент времени. Пусть X – непрерывная случайная величина, равная времени ожидания поезда пассажиром, пришедшим на станцию в случайный момент времени. Для X найти математическое ожидание M(X) и дисперсию D(X).
3.7.29. Поезда метро идут через данную станцию с интервалом две минуты. Пассажиры приходят на станцию независимо друг от друга. В данный поезд село 75 пассажиров. Найти приближенно вероятность того, что суммарное время ожидания пассажиров превосходит один час.
3.7.30. Вероятности попадания стрелка в десятку, девятку, восьмерку и семерку равны соответственно 0,4; 0,3; 0,2 и 0,1. Приближенно найти вероятность следующего события A: при 25 выстрелах стрелок наберет от 220 до 240 очков (из 250 возможных).
