Математическая модель нарушителя. Определение коэффициента готовности нарушителя осуществить атаку.

В первую очередь необходимо ввести количественную меру сложности атаки (сложности реализации угрозы атаки), поскольку в общем случае следует говорить о том, готов ли (заинтересован ли и может) нарушитель реализовать атаку определенной сложности. При этом необходимо учитывать, что как уязвимости, создающие угрозу атаки, так и собственно угрозы атаки по своей сути разнородны, количественная же мера должна быть единой. Обратимся к основам теории информации (в интересующей нас здесь ее части […]), понимая, что для осуществления успешной атаки на отдельно взятую уязвимость, нарушитель должен обладать соответствующей информацией в отношении этой уязвимости - информацией о том, что такая уязвимость выявлена и не устранена, т.е. неким количеством информации в отношении уязвимости. Т.к. нас интересует исключительно вероятность того, что уязвимость присутствует в информационной системе, при этом возможны два исхода события – уязвимость присутствует, либо нет, количество информации в отношении уязвимости в данном случае следует рассматривать, как вероятностную меру.

Замечание. Сложность практической реализации атак на те уязвимости, которые требуют разработки соответствующих программных средств (эксплоитов) для их эксплуатации при реализации атаки, учитывается при задании соответствующего параметра уязвимости - интенсивности возникновения уязвимости 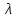[1]. При задании этого параметра на основании анализа соответствующей статистики уязвимостей должна рассматриваться только та часть уязвимостей, для которых подобные эксплоиты были разработаны и использованы.

В соответствии с [3], вероятностная мера количества информации I (в рассматриваемом случае - в одном сообщении) определяется по формуле:

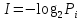
где 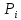– вероятность i -го исхода.

В нашем случае неопределенность можно рассматривать в отношении любой уязвимости, которая может использоваться нарушителем при осуществлении атаки, вероятность присутствия которой в системе определяется, как 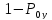. Нарушитель, для осуществления успешной атаки на уязвимость, должен обладать соответствующей информацией, в отношении присутствия уязвимости в системе, т.е. получить сведения, уменьшающие неопределенность в отношении данной уязвимости [5]. Очевидно, что чем выше для уязвимости значение 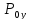(в общем случае уязвимость реже возникает и за меньшее время устраняется), тем сложнее осуществить атаку на уязвимость.

С учетом сказанного сложность атаки на уязвимость, обозначим ее 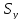, может интерпретироваться, как вероятностная мера количества информации 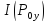, которым должен обладать злоумышленник для реализации атаки на эту уязвимость, как следствие, может быть определена следующим образом:

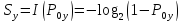
Корректность использования данной метрики для оценки сложности атаки на уязвимость обосновывается использованием логарифмической функции (в нашем случае по основанию 2, поскольку у события возможны только два исхода), позволяющей соответствующим образом учесть нелинейность функции изменения сложности атаки на уязвимость от изменения вероятности : =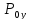

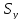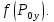
Проиллюстрируем сказанное примером, для чего сравним сложность атаки на две уязвимости, пусть для одной из них значение характеристики 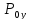составляет 0,7, а для другой 0,99. Видим, что в первом случае 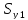=1,74, во втором случае 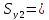6,64, т.е. реализация успешной атаки на вторую уязвимость для злоумышленника в 3,82 раза сложнее, чем на первую (ему понадобится в 3,82 раза больше количества информации об уязвимости (с целью снятия неопределенности в отношении наличия в системе этой уязвимости) для осуществления успешной атаки на вторую уязвимость, чем на первую.

Замечание. Единица сложности атаки на уязвимость: 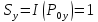задается условием: 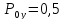, определяющим то, что уязвимость с равной вероятностью присутствует в системе, либо нет.

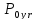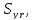Поскольку угрозу атаки создает соответствующая совокупность выявленных и не устраненных в системе уязвимостей, сложность атаки для нарушителя в общем случае определяется совокупной сложностью атак на каждую создающую угрозу атаки уязвимость. Если рассмотреть атаку как последовательность использования нарушителем выявленных и не устраненных в системе уязвимостей, имеющих характеристики и r=1,…,R, можно вести количественную характеристику сложности атаки 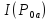, обозначим е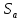е , где 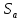= 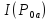, которая определяется количеством информации, которым должен обладать злоумышленник, для осуществления успешной атаки, угрозу которой создаютR выявленных в системе и не устраненных уязвимостей:

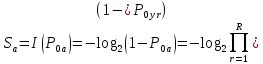
Используя же соответствующее свойство логарифмов, можем записать:

При этом информация, получаемая нарушителем, рассматривается с точки зрения ее полезности (ценности) для достижения потребителем информации поставленной практической цели - в нашем случае - для осуществления злоумышленником успешной атаки на информационную систему.

Универсальность данной количественной оценки обусловливается тем, что она позволяет, сравнивать между собою сложности реализации разнородных атак, основанных на различных принципах реализации, в общем случае использующих совершенно различные уязвимости.

Коэффициент готовности нарушителя осуществить атаку 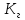требуется определять применительно к конкретной информационной системе при проектировании для нее системы защиты. На практике при решении задачи проектирования может рассматриваться (и, как правило, рассматривается) некая подобная информационная система (аналог), характеризуемая обработкой аналогичной информации, что и определяет заинтересованность и возможности нарушителя. В отношении аналога естественно есть соответствующая статистика реализованных ( в том числе и отраженных) на информационную систему атак в процессе ее эксплуатации.

С учетом сказанного математическая модель нарушителя (количественная интегральная оценка заинтересованности и возможности реализации злоумышленником атаки на конкретную информационную систему) может быть представлена следующим образом:

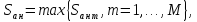
где 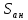– максимальная сложность реализованных (с учетом и отраженных) в подобной информационной системе атак, характеризуемых 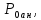определяемая на множестве выявленных совершенных атак на подобную информационную систему (аналог) в процессе ее эксплуатации .

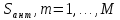Имея значение характеристики 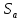– характеристика сложности реализации атаки на информационную систему, для которой проектируется система защиты, и значение характеристики 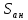- характеристика максимальной сложности реализованных (в том числе, и отраженных) в подобной информационной системе атак, можно определить искомую характеристикукоэффициента готовности нарушителя осуществить атаку сложности 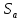на конкретную информационную систему (для которой проектируется система защиты) :

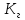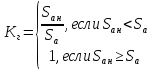
Исходя же из того, что:

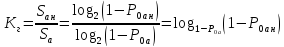
коэффициент 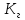может интерпретироваться, как значение степени, в которую надо возвести значение вероятности осуществления атаки на информационную систему 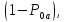для получения значения вероятности атаки, которую может успешно реализовать нарушитель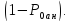

Замечание. Готовность злоумышленника к осуществлению атаки может интерпретироваться, как своего рода "уязвимость" системы, используемая данной атакой. Как следствие, данная уязвимость, наряду с иными уязвимостями, создающими угрозу атаки, может в качестве отдельной вершины быть включена в орграф угрозы атаки, см. рис.1, характеризуемой («взвешенной») значением вероятности того, что информационная система готова к безопасной эксплуатации в отношении этой уязвимости, определяемой в данном случае, как 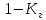, и соответственно в качестве дополнительного элемента в соответствующую схему параллельного резервирования уязвимостей.

Заключение.