Математическая модель угроз безопасности информационных ресурсов

На основе анализа существующих классификационных схем, перечисленных выше, нами были разработаны новые многокритериальные классификации криптосистем, атак и злоумышленников (см. рис. 7.3 - 7.5 ). Далее мы покажем, как применение разработанных классификационных схем для построения ABC -модели позволяет провести всесторонний анализ угроз безопасности информационных ресурсов, защищенных с использованием криптографических средств.

Пусть 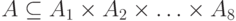- множество параметрических моделей атак, где 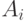( 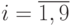) - множество значений i-го параметра модели атаки, определяющего тип атаки в соответствии с критериями разработанной классификации. Каждая модель 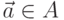представляет собой вектор 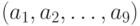, где .

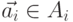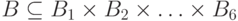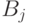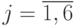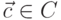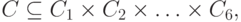
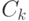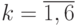Аналогично, параметрическая модель злоумышленника задается в виде вектора , где , ( ) - множество значений j-го параметра модели злоумышленника, модель криптосистемы - , где ( ) - множество значений k-го параметра модели криптосистемы в соответствии с многокритериальной классификацией. Заметим, что множества значений параметров модели атаки, злоумышленника и криптосистемы конечны.

При дальнейшем изложении для краткости слово "модель" применительно к модели атаки, модели злоумышленника и модели криптосистемы будем опускать.

С каждой атакой будем связывать значение риска, вычисляемое по общеизвестной формуле на основе двух факторов - вероятности происшествия и тяжести возможных последствий:

Риск = Влияние Вероятность

Обозначим через функцию, задающую уровень риска, связанного с атакой 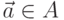в условиях, когда она может быть применена злоумышленником для взлома криптосистемы .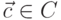

Пусть 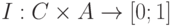- функция влияния (от англ. impact - влияние, воздействие). Под влиянием мы будем понимать степень ущерба от применения атаки 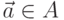к криптосистеме .

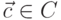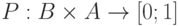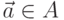Пусть - вероятность того, что злоумышленник предпримет атаку , т.е. обладает ресурсами для ее осуществления и сочтет эту атаку целесообразной.

Тогда функция риска выражается следующим образом:

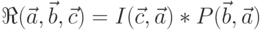
Определим функцию 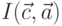. Для этого рассмотрим семейство функций 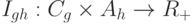, , , где 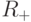- множество неотрицательных действительных чисел. Здесь функция 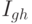задает уровень взаимного влияния параметра криптосистемы 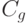и параметра атаки :

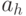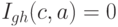· , если атака со значением параметра 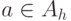не применима к криптосистеме со значением параметра ;

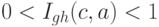· , если значение параметра криптосистемы снижает вероятность успешного применения атаки со значением параметра ;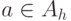

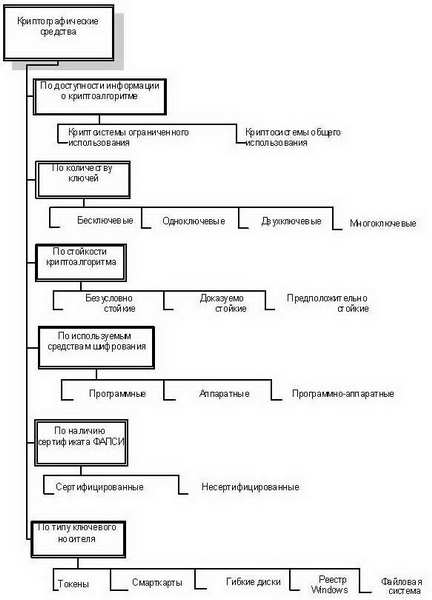
Рис. 7.3.Классификация криптосистем

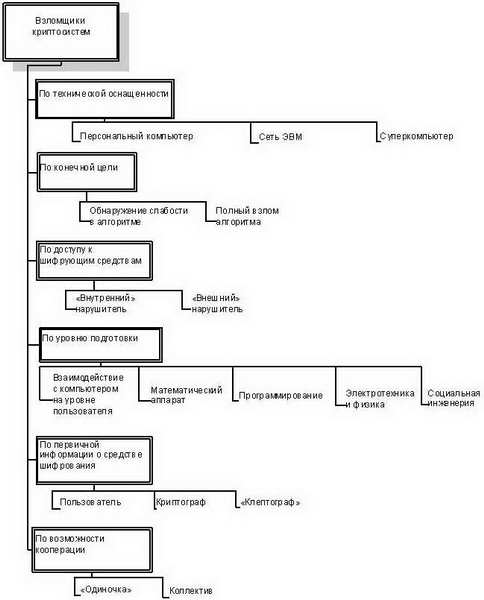
Рис. 7.4.Классификация злоумышленников

увеличить изображение
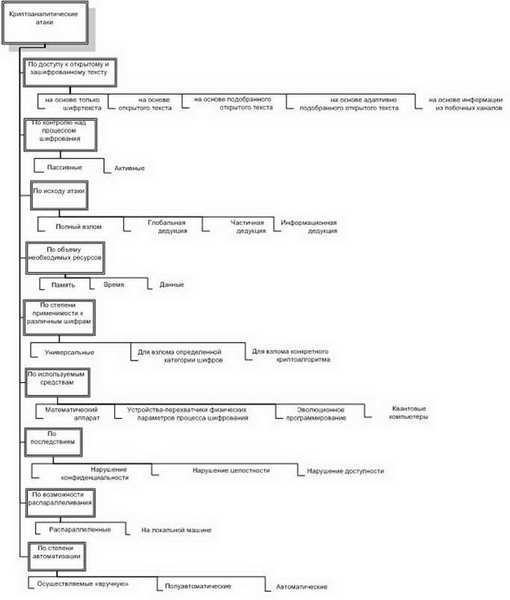
Рис. 7.5.Классификация криптоатак

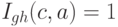· , если значение параметра криптосистемы не влияет на применимость атаки с параметром ;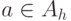

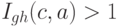· , если значение параметра криптосистемы указывает на то, что атака с параметром 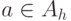применима для ее взлома.

Например, если исследуемый алгоритм шифрования реализован в аппаратном обеспечении, это повышает вероятность применения для взлома криптосистемы атак по побочным каналам [7.37] (это вид криптографических атак, использующих информацию, которая может быть получена с устройства шифрования и не является при этом ни открытым текстом, ни шифртекстом). Уровень взаимного влияния параметров криптосистемы и атаки определяется на основе экспертных оценок.

Обозначим через 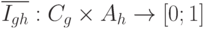нормированную функцию:

Тогда уровень ущерба от применения атаки 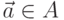к криптосистеме 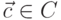вычисляется по следующей формуле:

,

где атака и криптосистема заданы параметрам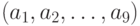и и 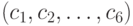соответственно. Заметим, что уровень влияния всех параметров криптосистемы на применимость атаки с заданным значением -го параметра в этой формуле вычисляется по мультипликативному критерию: 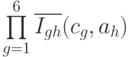. Если значение хотя бы одного из параметров криптосистемы противоречит возможности применения атаки, то результатом оценки применимости атаки к криптосистеме будет нулевое значение, что соответствует нулевому уровню ущерба от атаки.

Функция , определяющая зависимость между параметрами 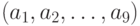атаки и 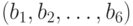злоумышленника, выражается аналогично функции 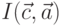. В качестве иллюстрации взаимосвязи параметров злоумышленника и атаки можно привести следующий пример: наличие у предполагаемого взломщика доступа к распределенным вычислительным ресурсам повышает вероятность применения метода "грубой силы" и, вообще говоря, любой атаки, легко поддающейся распараллеливанию.

Таким образом, общая формула для определения уровня риска, связанного с атакой 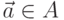в условиях, когда эта атака может быть применена злоумышленником для взлома криптосистемы 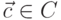, имеет вид:

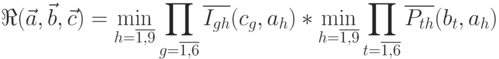
Будем считать, что криптосистема 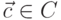подвержена атаке 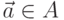в условиях, когда ей угрожает злоумышленник , если 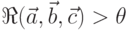, т.е. связанный с ней уровень риска превышает заданное пороговое значени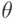е , где . Допустимый уровень риска 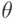является настраиваемым параметром ABC -модели угроз криптосистемы. Значение 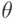задается с учетом двух критериев:

· критичности защищаемых данных;

· временных и других ресурсов, доступных специалисту, который осуществляет аудит системы.

В общем случае:

· криптосистема может включать несколько подсистем (например, генератор ключей и симметричный шифратор), к каждой из которых применим свой набор атак;

· на криптосистему может нападать несколько злоумышленников.

Множество атак, которым подвержена криптосистема, состоящая из подсистем 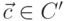( 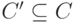), в условиях, когда ей угрожают злоумышленники 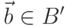( 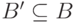), будем определять по формуле , где 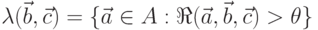при заданном уровне риска. Для оценки защищенности криптосистемы необходимо с использованием инструментальных средств оценить ее способность противостоять атакам, входящим в множество .

В описанной математической модели сделаны следующие допущения:

· не учитывается зависимость параметров атаки от сочетания параметров криптосистемы, хотя влияние каждого параметра принимается во внимание;

· не учитывается возможность совместных действий со стороны взломщиков различных типов, хотя можно задать модель нападения со стороны однородного коллектива злоумышленников.

Исправление ABC -модели с учетом указанных допущений привело бы к ее значительному усложнению. Вопрос о том, насколько эти допущения снижают точность моделирования угроз безопасности, подлежит дальнейшим исследованиям.

Важно отметить, что разработанная классификационная схема для построения моделей атак на алгоритмы шифрования с небольшими модификациями применима и для моделирования атак на криптопротоколы. Возможность использования ABC -модели угроз для комплексного исследования криптосистемы является важной, т.к. вопрос совместного функционирования криптопротоколов и шифров в рамках одной криптосистемы, как показано в [7.27], до сих пор был мало изучен.