Глава 3. Введение в динамику механической системы

Дифференциальные уравнения движения механической системы в декартовых координатах

Механической системойбудем называть выбранную совокупность материальных точек, движение которых взаимосвязано.

Силы, действующие на точки механической системы подразделяются на внешние (обозначаются 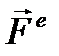) и внутренние (обозначаются ).

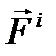Внешними называются силы, действующие на точки механической системы со стороны материальных объектов, не включенных в систему.

Внешние силы оказывают основное влияние на движение механической системы. В задачах не космического масштаба к их числу относятся сила тяжести, реакции внешних связей и другие заданные в условии задачи внешние воздействия.

Внутренними называются силы взаимодействия между точками механической системы.

Следует отметить, что внутренние силы действуют в механической системе попарно и подчиняются закону равенства действия и противодействия.

При дальнейшем изучении динамики механической системы важное значение имеет следующая теорема об основных свойствах внутренних сил.

Теорема

При любом движении механической системы в любой момент времени главный вектор внутренних сил системы и их главный момент, вычисленный относительно любого центра, равны нулю.

Доказательство

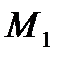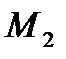Отметим, что внутренние силы в механической системе действуют попарно и подчиняются аксиоме равенства действия и противодействия.. Рассмотрим две такие внутренние силы взаимодействия точек и механической системы (см. рис. 8).

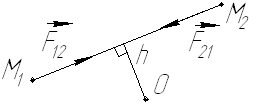
Рис. 8

Очевидно, что их геометрическая сумма равна нулю:

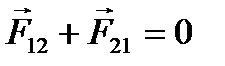
и геометрическая сумма их векторных моментов относительно произвольной точки О тоже равна нулю:

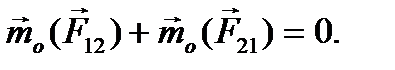
Отсюда следует утверждение теоремы.

Обозначим геометрическую сумму всех внутренних сил, действующих на точку системы с номером k, через 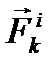, геометрическую сумму всех внешних сил, действующих на эту точку, через 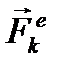. Число точек в механической системе обозначим через n. Тогда утверждение сформулированной теоремы может быть записано в виде двух векторных равенств:

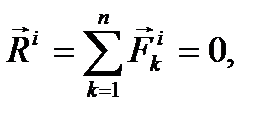
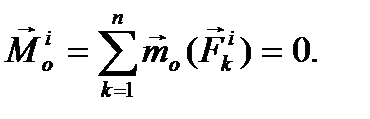(17)

После введения этих обозначений запишем основное уравнение динамики для каждой точки механической системы в виде:

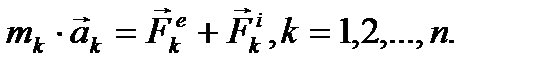(18)

Систему из n уравнений (18) называют дифференциальными уравнениями движения механической системы в векторной форме. Если векторные равенства (18) записать в проекциях на оси декартовой системы координат, то получим:

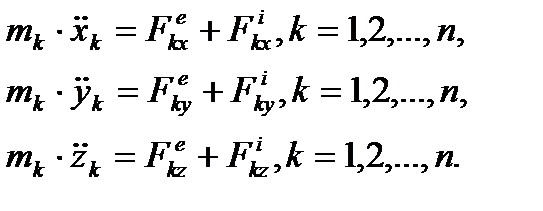(19)

Систему уравнений (19) называют дифференциальными уравнениями движения механической системы в декартовых координатах. Можно записывать векторные равенства (18) в проекциях на другие оси координат. Решение системы дифференциальных уравнений (19) позволяет детально изучить движение каждой точки механической системы. Однако эта задача исключительно трудна даже в простейших случаях. Поэтому уравнения (18), (19) для решения практических задач не используются. С их помощью можно вывести более простые соотношения, называемые общими теоремами динамики, которые не позволяют детально изучить движение каждой точки системы, но дают возможность найти некоторые важные характеристики движения. В механике рассматриваются 4 общие теоремы динамики:

¾ теорема о движении центра масс,

¾ теорема об изменении количества движения,

¾ теорема об изменении кинетического момента,

¾ теорема об изменении кинетической энергии.

Эти теоремы будут рассмотрены далее в главе 4.