Локальный поиск с чередующимися окрестностями

Идея этого подхода предложена Н. Младеновичем и П. Хансеном в 1997 г. [35]. Она состоит в систематическом изменении функции окрестности и соответствующем изменении ландшафта в ходе локального поиска. Существует много вариантов ее реализации, особенно для задач большой размерности. Легкость адаптации к различным моделям и высокая эффективность, особенно в сочетании с другими метаэвристиками, объясняет ее конкурентоспособность при решении NP-трудных задач.

Обозначим через , конечное множество функций окрестностей, предварительно выбранных для локального поиска. Предлагаемый алгоритм опирается на следующие три тезиса.

- Локальный минимум для одной окрестности не обязательно является локальным минимумом для другой.

- Глобальный минимум является локальным минимумом относительно любой окрестности.

- Для многих задач дискретной оптимизации локальные минимумы относительно одной или нескольких окрестностей расположены достаточно близко друг к другу.

Последний тезис является эмпирическим. Он позволяет сузить область поиска глобального оптимума, используя информацию об уже обнаруженных локальных оптимумах. Именно эта идея лежит в основе алгоритмов связывающих путей, различных операторов скрещивания для генетических алгоритмов и многих других подходов. Алгоритм чередующихся окрестностей неявно использует этот тезис. Общая схема алгоритма может быть представлена следующим образом.

Алгоритм VNS

1. Выбрать окрестности , и начальное решение .

2. Повторять, пока не выполнен критерий остановки.

2.1. Положить

2.2. Повторять, пока :

(a) Выбрать случайным образом.

(b) Применить локальный поиск с начального решения 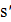. Полученный локальный оптимум обозначим . (c) Если то иначе

3. Предъявить наилучшее найденное решение

В качестве критерия остановки может использоваться максимальное время счета или число итераций без смены лучшего найденного решения. Наряду с последовательным порядком смены окрестностей могут использоваться различные групповые стратегии. Случайный выбор на шаге 2.2 (a) применяется во избежание зацикливания. На шаге 2.2 (b) локальный поиск может использовать различные алгоритмы SA, TS и др.

Существует много вариантов этой схемы. Например, на шаге 2.2 (c) переход осуществляется только при уменьшении значения целевой функции. Это условие можно заменить по аналогии с алгоритмом имитации отжига и разрешать движение в точку с большим значением целевой функции с некоторой вероятностью, зависящей от этого ухудшения. Идею наискорейшего спуска можно осуществить путем следующих изменений. Вместо шага 2.2, на котором выполняется переход согласно k-й окрестности, следует выбрать наилучший переход по всем рассматриваемым окрестностям. Другой способ состоит в модификации шага 2.2 (a) и выборе не случайного решения, а наилучшего в k-й окрестности. Порядок смены окрестностей тоже может варьироваться.

На рис. 5.23 показано типичное поведение алгоритма VNS. Высокие пики на последних итерациях соответствуют переходам на шаге 2.2 (a), где выбирается случайным образом соседнее решение. Несмотря на заметное ухудшение по целевой функции, локальный поиск на шаге 2.2.(b) быстро возвращается к хорошим решениям. Тенденция к последовательному улучшению рекорда хорошо видна на этом рисунке.

Итерации

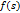Рисунок-5.23. Поведение алгоритма VNS

Генетические алгоритмы

Идея генетических алгоритмов заимствована у живой природы и состоит в организации эволюционного процесса, конечной целью которого является получение оптимального решения сложной комбинаторной задачи. Разработчик генетических алгоритмов выступает в данном случае как «создатель», который должен правильно установить законы эволюции, чтобы достичь этой цели. Впервые эти нестандартные идеи были применены к решению оптимизационных задач в середине 70-х гг. прошлого столетия. Примерно через десять лет появились первые теоретические обоснования этого подхода. На сегодняшний день генетические алгоритмы доказали свою конкурентоспособность при решении многих NP-трудных задач, особенно в приложениях, где математические модели имеют сложную структуру, а применение стандартных методов типа ветвей и границ, динамического или линейного программирования крайне затруднено.

Стандартный генетический алгоритм начинает свою работу с формирования начальной популяции – конечного набора допустимых решений задачи. Эти решения могут быть выбраны случайным образом или получены с помощью конструктивных алгоритмов. Выбор начальной популяции не имеет значения для сходимости процесса в асимптотике, однако формирование «хорошей» начальной популяции (например, из множества локальных оптимумов) может заметно сократить время достижения глобального оптимума.

На каждом шаге эволюции с помощью вероятностного оператора селекции выбираются два решения, родители . Оператор скрещивания по этим решениям строит новое решение 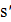, которое затем подвергается небольшим случайным модификациям. Их принято называть мутациями. Затем решение добавляется в популяцию, а решение с наименьшим значением целевой функции удаляется из популяции. Общая схема такого алгоритма может быть записана следующим образом.

Алгоритм GA

1. Выбрать начальную популяцию.

2. Повторять, пока не выполнен критерий остановки.

2.1. Выбрать родителей из популяции.

2.2. Построить новое решение по решениям .

2.3. Модифицировать .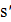

2.4. Обновить популяцию

3. Предъявить наилучшее решение в популяции

Остановимся подробнее на основных операторах этого алгоритма: селекции, скрещивании и мутации. Среди операторов селекции наиболее распространенными являются два вероятностных оператора: пропорциональной и турнирной селекции. При пропорциональной селекции вероятность выбрать решение в качестве одного из родителей зависит от качества этого решения: чем меньше значение целевой функции, тем выше вероятность, а сумма вероятностей равна 1. При турнирной селекции формируется случайное подмножество из элементов популяции, и среди них выбирается один элемент с наименьшим значением целевой функции. Турнирная селекция имеет определенные преимущества. Она не теряет своей избирательности, когда в ходе эволюции все элементы популяции становятся примерно равными по значению целевой функции. Операторы селекции строятся таким образом, чтобы с ненулевой вероятностью любой элемент популяции мог бы быть выбран в качестве одного из родителей. Более того, допускается ситуация, когда оба родителя представлены одним и тем же элементом популяции. Возвращаясь к алгоритму VNS, представляется разумным брать в качестве одного из родителей наилучший элемент популяции.

Как только два решения выбраны, к ним применяется вероятностный оператор скрещивания (crossover). Существует много различных версий этого оператора, среди которых простейшим, по-видимому, является однородный оператор. По родительским решениям он строит новое решение, присваивая каждой координате этого вектора с вероятностью 0,5 соответствующее значение одного из родителей. Если родительские вектора совпадали, скажем, по первой координате, то новый вектор «унаследует» это значение. Геометрически, для булевых векторов, оператор скрещивания случайным образом выбирает в гиперкубе вершину 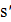, которая принадлежит минимальной грани, содержащей вершины . Можно сказать, что оператор скрещивания старается выбрать новое решение где-то между родительскими, полагаясь на удачу. Более аккуратная процедура могла бы выглядеть таким образом. Новое решение выбирается как оптимальное решение исходной задачи на соответствующей грани гиперкуба. Если расстояние между достаточно велико, то задача оптимального скрещивания может совпадать с исходной. Тем не менее, даже приближенное решение этой задачи вместо случайного выбора заметно улучшает работу генетического алгоритма.

Оператор мутации с заданной вероятностью меняет значение каждой координаты на противоположное. Например, вероятность того, что вектор в ходе мутации перейдет в вектор равна Таким образом, с ненулевой вероятностью новое решение 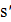может перейти в любое другое решение, что и объясняет асимптотические свойства алгоритма. Отметим, что модификация решения может состоять не только в случайной мутации, но и в частичной перестройке решения алгоритмами локального поиска. Применение локального улучшения позволяет генетическому алгоритму сосредоточиться только на локальных оптимумах. Множество локальных оптимумов может оказаться экспоненциально большим, и на первый взгляд такой вариант алгоритма не будет иметь преимуществ. Однако экспериментальные исследования распределения локальных оптимумов свидетельствуют о высокой концентрации их в непосредственной близости от глобального оптимума. Это наблюдение отчасти объясняет работоспособность генетических алгоритмов. Если в популяции собираются локальные оптимумы, которые сконцентрированы в одном месте, и очередное решение 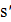выбирается где-то между двумя произвольными локальными оптимумами, то такой процесс имеет много шансов найти глобальный оптимум.

расстояние

Рисунок-5.24. Распределение локальных оптимумов

На рис. 5.24 показаны результаты численных экспериментов для задачи коммивояжера при . Каждая точка на рисунке соответствует локальному оптимуму по окрестности 2-замена. Ось показывает значение целевой функции для локальных оптимумов.

По оси откладывается расстояние от локального оптимума до глобального. Максимально возможное расстояние равно 532. Однако среднее расстояние не превышает 200. Это означает, что все локальные оптимумы имеют более 300 общих ребер с глобальным оптимумом. Они все достаточно близки друг к другу [36].

В заключение этой главы хочется еще раз подчеркнуть тот факт, что разработка численных методов для решения NP-трудных задач дискретной оптимизации дает широкий простор для творчества. Учет специфики решаемой задачи может подсказать структуру окрестностей, выбор схемы и идею самого алгоритма, но единого наилучшего для всех задач метода построить не удастся, и теоремы о небесплатных завтраках (No Free Lunch Theorems) – ясное тому подтверждение.

Упражнения

Упражнение 5.1. При построении примитивной нижней оценки для задачи коммивояжера можно сначала вычислять плату за въезд, в потом плату за выезд, но можно и наоборот (сначала плату за выезд, а потом плату за въезд). Покажите, что эти два варианта могут давать разные нижние оценки.

Упражнение 5.2.Покажите, что нижняя оценка линейного программирования из раздела 5.3.2 не хуже оптимального значения
в целочисленной задаче о назначениях.

Упражнение 5.3.Приведите пример неотрицательной матрицы расстояний, для которой разница между оптимумом в задаче коммивояжера и оптимумом в задаче о назначениях была бы сколь угодно велика.

Упражнение 5.4.Усовершенствуйте полиномиальный алгоритм для задачи о назначениях, понизив его трудоемкость до O(n³).

Упражнение 5.5.Приведите пример неотрицательной матрицы расстояний, для которой разница между оптимумом в задаче коммивояжера и длиной минимального 1-дерева была бы сколь угодно велика.

Упражнение 5.6.Покажите, что минимальные 1-деревья дают нижнюю оценку для задачи коммивояжера, которая не больше оптимума задачи о назначениях.

Упражнение 5.7.Докажите, что оценка 3/2 для алгоритма Кристофидеса – Сердюкова является неулучшаемой.

Упражнение 5.8.Известно, что выбор наилучшего эйлерова цикла при построении приближенного алгоритма с оценкой 3/2 по Кристофидесу и Сердюкову является NP-трудной задачей. Постройте для ее решения генетический алгоритм, алгоритм поиска с запретами и алгоритм имитации отжига.

Упражнение 5.9.Для задачи коммивояжера разработайте гибридную схему генетического алгоритма и поиска с запретами, генетического алгоритма и имитации отжига, локального поиска с чередующимися окрестностями и поиска с запретами.

Упражнение 5.10.Постройте генетический алгоритм и алгоритм поиска с чередующимися окрестностями для задачи Штейнера.

Упражнение 5.11.В открытой задаче коммивояжера требуется посетить все города, но не возвращаться в исходный город. Как решить эту задачу с помощью алгоритма для классической задачи коммивояжера?

Упражнение 5.12.Покажите, что открытая задача коммивояжера является NP-трудной.

Упражнение 5.13.Сформулируйте задачу обхода конем всех полей шахматной доски как открытую задачу коммивояжера.

Упражнение 5.14.В задаче коммивояжера на узкое место требуется минимизировать длину максимального ребра вместо суммы длин ребер. Запишите эту задачу в терминах целочисленного линейного программирования.

Упражнение 5.15.Покажите, что задача коммивояжера на узкое место является NP-трудной.

Упражнение 5.6.Предположим, что коммивояжер должен посетить город сразу (не обязательно сразу) после города . Запишите эту задачу в терминах целочисленного линейного программирования.

Упражнение 5.17.Предположим, что коммивояжер должен посещать город i не раньше момента времени и не позже
Если он приезжает раньше срока, то вынужден ждать. Запишите эту задачу в терминах целочисленного линейного программирования.

Упражнение 5.18.Предположим, что коммивояжер посещает города с целью доставки грузов. В городе находится склад.

В каждый город требуется доставить единиц груза, . У коммивояжера имеется транспортное средство грузоподъемностью и для всех . Коммивояжер может возвращаться на склад, брать груз и снова направляться в непосещенные города. Его цель ­­­– минимизировать пройденное расстояние, посетить все города и вернуться на склад. Запишите эту задачу в терминах целочисленного линейного программирования.

Упражнение 5.19.В условиях предшествующей задачи будем предполагать, что коммивояжер может посещать любой город много раз и условие может нарушаться. Запишите эту задачу
в терминах частично-целочисленного линейного программирования.

Упражнение5.20.Покажите, что задача коммивояжера с экспоненциальной окрестностью из раздела 5.4.4 принадлежит классу PLS.

Упражнение 5.21.Приведите пример задачи распознавания,
которая не принадлежит классу NP (в предположении, что P ≠ NP).

Упражнение 5.22.Приведите пример задачи распознавания,
которая не принадлежит классу co-NP (в предположении, что P ≠ NP).

Упражнение 5.23.Приведите пример задачи распознавания, которая не принадлежит классам NP и co-NP (в предположении, что P ≠ NP).

Упражнение 5.24.Покажите, что если оптимизационная задача является NP-трудной, то существование для нее точной полиномиально проверяемой окрестности влечет совпадение классов NP и co-NP.

Упражнение 5.25.Покажите, что если оптимизационная задача является NP-трудной в сильном смысле, то существование для нее точной полиномиально проверяемой окрестности влечет совпадение классов P и NP.

Библиографический список

1. Кузнецов Ю.Н., Кузубов В.И. и Волощенко А.Б. Математическое программирование. – М.: Высшая школа, 1980. 40-55 с.

2. Калижанова А.У., Айткулов Ж.С. Моделирование систем управления. – Алматы.: КазНТУ им.К.И.Сатпаева. 2003. –32 с.

3. Калижанова А.У., Айткулов Ж.С. Методы теории систем. – Алматы.: КазНТУ им.К.И.Сатпаева. 2003. –37 с.

4. Кристофидес Н. Теория графов. Алгоритмический подход. М: Мир, 1978.

5. Wichmann B. A. Ackermann’s function: a study in the efficiency of calling procedures // BIT. 1976. Vol. 16. P.103–110.

6. Monma C., Suri S. Transitions in geometric minimum spanning trees // Discrete ans Computational Geometry. 1992. Vol. 8, N 3. P. 265–293.

7. Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. М.: Мир, 1982.

8. Дементьев В. Т., Ерзин А. И., Ларин Р. М. и др. Задачи оптимизации иерархических структур. Новосибирск: Изд-во Новосибирского ун-та, 1996.

9. Robins G., Zelikovsky A. Improved Steiner tree approximation in graphs // Proc. 10th Ann. ACM-SIAM Symp. on Discrete Algorithms, ACM-SIAM, 2000. P. 770–779.

10. Hanan M. On Steiner’s problem with rectilinear distance // SIAM J. Applied Math. 1966. Vol. 14. P. 255–265.

11. Hwang F. K. On Steiner minimal trees with rectilinear distance // SIAM J. Applied Math. 1976. Vol. 30, N 1. P. 104–114.

12. Zelikovsky A. Z. An 11/8-approximation algorithm for the Steiner problem on networks with rectilinear distance // Janos Bolyai Mathematica Societatis Conf.: Sets, Graphs, and Numbers, 1992.
P. 733–745.

13. Erzin A. I., Cho J. D. A Deep-Submicron Steiner Tree // Mathematical and Computer Modeling. 2000. Vol. 31. P. 215–226.

14. Ерзин А. И., Чо Д. Д. Задача построения синхронизирующего сигнального дерева // Автоматика и телемеханика. Vol. 2003. № 3. С. 163–176.

15. Ерзин А. И. Введение в исследование операций: учеб. пособие. Новосибирск: НГУ, 2006.

16. Korte B, Vygen J. Combinatorial optimization. Berlin: Springer, 2007.

17. Кормен Т., Лейзерсон Ч., Ривест Р. и др. Алгоритмы. Построение и анализ. 2 издание. М.: Вильямс, 2009.

18. Deineko V., Tiskin A. Fast minimum-weight double-tree shortcutting for metric TSP: is the best one good enough? // ACM Journal on Experimental Algorithmics. 2009. Vol. 14. N 4.6.

19. Сигал И. Х., Иванова А. П. Введение в прикладное дискретное программирование: модели и вычислительные алгоритмы. М.: ФИЗМАТЛИТ, 2007.

20. Пападимитриу Х., Стайглиц К. Комбинаторная оптимизация. Алгоритмы и сложность. М.: Мир, 1985.

21. Алексеева Е. В. Построение математических моделей целочисленного линейного программирования. Примеры и задачи. Новосибирск: НГУ, 2012.

22. Yannakakis M. Computational complexity. In: Aarts E., Lenstra J. (Eds.) Local search in combinatorial optimization. NY: Wiley, 1997.

23. Кочетов Ю. А. Методы локального поиска для дискретных задач размещения Модели и алгоритмы. Saarbrucken: Lambert Academic Publishing, 2011.

24. Кочетов Ю. А. Вычислительные возможности локального поиска в комбинаторной оптимизации // Журнал вычислительной математики и математической физики. 2008. Т. 48, № 5. С. 788–807.

25. Grover L. K. Local search and the local structure of NP-complete problems // Operations Research Letters. 1992. Vol. 12, N 4. P. 235–244.

26. Angel E., Zissimopoulos V. On the classification of NP-complete problems in terms of their correlation coefficient // Discrete Appl. Math. 2000. Vol. 99. P. 261–277.

27. Burkard R. E., Deineko V. G., Woeginger G. J. The traveling salesman problem and the PQ-tree // Lecture Notes in Computer Science, Vol. 1084. Berlin: Springer, 1996. P. 490–504.

28. Gutin G. Exponential neighborhood local search for the traveling salesman problem // Comput. Oper. Res. 1999. Vol. 26. P. 313–320.

29. Gutin G., Yeo A. Small diameter neighborhood graphs for the traveling salesman problem: four moves from tour to tour // Comput. Oper. Res. 1999. Vol. 26. P. 321–327.

30. Talbi El-G. Metaheuristics: From Design to Implementation (Wiley Series on Parallel and Distributed Computing). Wiley, 2009.

31. Charon I., Hudry H. The noising methods. A survey. In: Ribeiro C. C., Hansen P. (eds.) Meta-heuristics: Advances and Trends in Local Search Paradigms for Optimization. Boston: Kluwer. Acad. Publ., 1998. P. 245–262.

32. Kirkpatrick S., Gelatt C. D., Vecchi M. P. Optimization by simulated annealing // Science. 1983. Vol. 220. P.671–680.

33. Кемени Дж., Снелл Дж. Конечные цепи Маркова. М.: Наука, 1970.

34. Glover F., Laguna M. Tabu Search. Dordrecht: Kluwer Acad. Publ., 1997.

35. Mladenović N., Hansen P. Variable neighbourhood search // Computers and Operations Research, 1997. Vol. 24. P. 1097–1100.

36. Boese K. D., Kahng A. B., Muddu S. A new adaptive multi-start technique for combinatorial global optimizations // Oper. Res. Lett. 1994. Vol. 16, N 2. P.101–114.

37. Wolsey L. A. Integer Programming. N. Y.: John Wiley & Sons, Inc, 1998.

38. Дасгупта С., Пападимитриу Х., Вазирани У. Алгоритмы (Перевод с английского А. С. Куликова под редакцией А. Шеня) М.: МЦНМО, 2014. – 320 с.

Учебное издание