Экспоненциальные окрестности
Одним из новых перспективных направлений в области локального поиска является исследование свойств окрестностей экспоненциальной мощности. Если лучшее решение в такой окрестности можно найти за полиномиальное время, то алгоритм локального поиска с такой окрестностью получает определенное преимущество перед остальными. Для задачи коммивояжера первые примеры таких окрестностей были предложены в работе [28]. Изложим, в качестве иллюстрации, идею одного из таких подходов. Этот пример наглядно показывает тесную связь между экспоненциальными окрестностями и полиномиально разрешимыми случаями задачи коммивояжера. Наличие такой связи, по-видимому, будет стимулировать поиск новых полиномиально разрешимых случаев для трудных комбинаторных задач, что в свою очередь может привести к дальнейшему прогрессу в области локального поиска.
Основная идея может быть представлена следующим образом. Предположим, что множество из 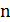 городов разбито на две части
городов разбито на две части  и
и  , так, что
, так, что 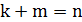 и
и 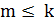 . Для удобства и простоты изложения добавим в первую группу
. Для удобства и простоты изложения добавим в первую группу 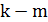 фиктивных городов
фиктивных городов 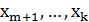 и рассмотрим окрестность
и рассмотрим окрестность 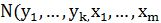 ), состоящую из всех циклов вида
), состоящую из всех циклов вида
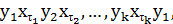
где 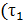 ,…,
,…, 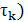 – произвольная перестановка
– произвольная перестановка 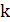 элементов. Содержательно, каждый такой цикл получается вставкой городов
элементов. Содержательно, каждый такой цикл получается вставкой городов 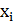 между парами городов
между парами городов 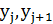 . Множество
. Множество 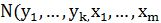 ) имеет экспоненциальную мощность
) имеет экспоненциальную мощность 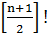 при
при 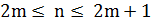 . Оптимальный тур в этом множестве может быть найден с помощью решения задачи о назначениях следующим образом.
. Оптимальный тур в этом множестве может быть найден с помощью решения задачи о назначениях следующим образом.
При 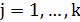 положим
положим
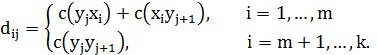
Введем переменные 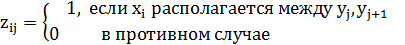
и рассмотрим задачу
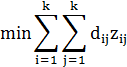
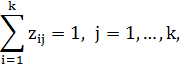
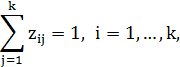
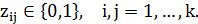
Оптимальное решение задачи определяет наилучшее размещение городов 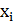 ,
, 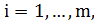 между городами
между городами 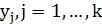 , то есть оптимальный тур в множестве
, то есть оптимальный тур в множестве 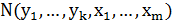 .
.
Заметим, что максимальная мощность окрестности 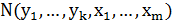 достигается при
достигается при 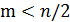 . Точнее, пусть
. Точнее, пусть 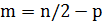 ,
, 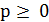 , целое,
, целое, 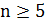 и
и 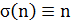 (mod 2). Для действительного числа
(mod 2). Для действительного числа 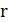 обозначим через
обозначим через 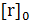 (соответственно
(соответственно 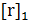 ) максимальное целое (полуцелое, то есть число вида
) максимальное целое (полуцелое, то есть число вида 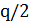 для нечетных
для нечетных 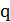 ), не превосходящее
), не превосходящее 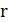 . Тогда максимальная мощность
. Тогда максимальная мощность 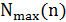 окрестности превосходит
окрестности превосходит 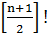 и, согласно [29], равна:
и, согласно [29], равна: 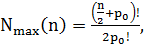 где
где 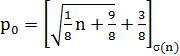 .
.
Применение этой формулы позволяет получить асимптотическое выражение для мощности окрестности.
Теорема 5.12. 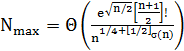 .
.
Перейдем теперь к наиболее интригующему свойству данной окрестности, связанному к расстоянием между турами в графе окрестностей. Оказывается, что с помощью множества 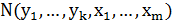 можно так определить новую окрестность, что расстояние между любыми двумя турами не будет превосходить 4 [30]. Сам факт, что максимальное расстояние между турами не зависит от размерности задачи, представляется удивительным. Более того, эта константа очень мала; всего 4 шага достаточно сделать, чтобы добраться из заданного решения до любого другого и, в частности, до оптимального. К сожалению, мы не знаем, в какую именно сторону нужно сделать эти четыре шага, иначе задача стала бы полиномиально разрешимой. Кроме того, мы не знаем, как много локальных оптимумов типа 2-замена или city-swap содержится в такой экспоненциальной окрестности. Тем не менее, факт ограниченности диаметра свидетельствует о больших потенциальных возможностях такой окрестности.
можно так определить новую окрестность, что расстояние между любыми двумя турами не будет превосходить 4 [30]. Сам факт, что максимальное расстояние между турами не зависит от размерности задачи, представляется удивительным. Более того, эта константа очень мала; всего 4 шага достаточно сделать, чтобы добраться из заданного решения до любого другого и, в частности, до оптимального. К сожалению, мы не знаем, в какую именно сторону нужно сделать эти четыре шага, иначе задача стала бы полиномиально разрешимой. Кроме того, мы не знаем, как много локальных оптимумов типа 2-замена или city-swap содержится в такой экспоненциальной окрестности. Тем не менее, факт ограниченности диаметра свидетельствует о больших потенциальных возможностях такой окрестности.
Пусть 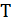 – произвольный гамильтонов цикл. Обозначим через
– произвольный гамильтонов цикл. Обозначим через 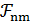 семейство всех подмножеств мощности
семейство всех подмножеств мощности 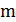 , состоящих из несмежных вершин цикла
, состоящих из несмежных вершин цикла 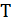 . Каждый элемент семейства
. Каждый элемент семейства
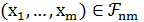 однозначно определяет множество циклов
однозначно определяет множество циклов 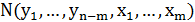 . Объединение таких множеств обозначим через
. Объединение таких множеств обозначим через 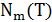 . Можно показать, что при фиксированном
. Можно показать, что при фиксированном 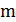 мощность семейства
мощность семейства 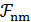 равна
равна 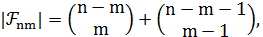 то есть выражается полиномом от
то есть выражается полиномом от 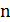 , и, следовательно, оптимальный цикл в множестве
, и, следовательно, оптимальный цикл в множестве 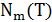 можно найти за полиномиальное время. Будем говорить, что цикл
можно найти за полиномиальное время. Будем говорить, что цикл 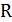 является соседним к циклу
является соседним к циклу 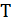 , если в цикле
, если в цикле 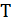 найдутся
найдутся 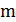 несмежных вершин
несмежных вершин 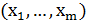 , таких,
, таких,
что 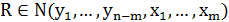 .
.
Теорема 5.13. При 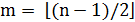 для любых циклов
для любых циклов 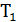 и
и 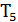 существуют такие циклы
существуют такие циклы 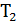 ,
, 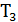 и
и 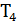 , что
, что 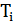 является соседним
является соседним
к 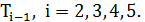
В общем случае при произвольных 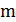 длина пути в графе окрестностей
длина пути в графе окрестностей 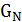 между двумя произвольными циклами ограничена сверху величиной
между двумя произвольными циклами ограничена сверху величиной 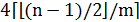 .
.
Метаэвристики
Идеи локального поиска получили свое дальнейшее развитие в так называемых метаэвристиках, то есть в общих схемах построения алгоритмов, которые могут быть применены практически к любой задаче дискретной оптимизации. Все метаэвристики являются итерационными процедурами, и для многих из них установлена асимптотическая сходимость наилучшего найденного решения к глобальному оптимуму. В отличие от алгоритмов с оценками, метаэвристики не привязываются к специфике решаемой задачи. Это достаточно общие итерационные процедуры, использующие рандомизацию и элементы самообучения, интенсификацию и диверсификацию поиска, адаптивные механизмы управления, конструктивные эвристики и методы локального поиска. К метаэвристикам принято относить методы имитации отжига (Simulated Annealing (SA)), поиск с запретами (Tabu Search (TS)), генетические алгоритмы (Genetic Algorithms (GA)) и эволюционные методы (Evolutionary Computation (EC)), а также поиск с чередующимися окрестностями (Variable Neighborhood Search (VNS)), муравьиные колонии (Ant Colony Optimization (ACO)), вероятностные жадные алгоритмы (Greedy Randomized Adaptive Search Procedure (GRASP)) и др. [31].
Идея этих методов основана на предположении, что целевая функция имеет много локальных экстремумов, а просмотр всех допустимых решений невозможен, несмотря на конечность их числа. В такой ситуации нужно сосредоточить поиск в наиболее перспективных частях допустимой области. Таким образом, задача сводится к выявлению таких областей и быстрому их просмотру. Каждая из метаэвристик решает эту проблему по-своему.
Метаэвристики принято делить на траекторные методы, когда на каждой итерации имеется одно допустимое решение и осуществляется переход к следующему, и на методы, работающие с семейством (популяцией) решений. К первой группе относятся TS, SA, VNS. Траекторные методы оставляют в пространстве поиска траекторию, последовательность решений, где каждое решение является соседним для предыдущего относительно некоторой окрестности. В методах TS, SA окрестность определяется заранее и не меняется в ходе работы. Целевая функция вдоль траектории меняется немонотонно, что позволяет «выбираться» из локальных экстремумов и находить все лучшие и лучшие приближенные решения. Элементы самоадаптации позволяют менять управляющие параметры алгоритмов, используя предысторию поиска. Более сложные методы, например, VNS, используют несколько окрестностей и меняют их систематически в целях диверсификации. Фактически, при смене окрестности происходит смена ландшафта. Сознательное изменение ландшафта, как, например, это происходит в методе шума (Noising method, [32]), благотворно сказывается на результатах поиска. Изучение ландшафтов, их свойств, например, изрезанности (ruggedness), позволяет давать рекомендации по выбору окрестностей.
Ко второй группе методов относятся GA, EC, ACO и др. На каждой итерации этих методов строится новое решение задачи, которое основывается уже не на одном, а на нескольких решениях из популяции. В генетических и эволюционных алгоритмах для этих целей используются процедуры скрещивания (crossover) и целенаправленных мутаций. В методах ACO применяется другая идея, основанная на сборе статистической информации о наиболее удачных найденных решениях. Эта информация учитывается в вероятностных жадных алгоритмах и подсказывает, какие именно компоненты решений (ребра графа, предприятия, элементы системы технических средств) чаще всего приводили ранее к малой погрешности. Методы этой группы, как правило, основаны на аналогиях в живой природе. Идея ACO является попыткой имитации поведения муравьев, которые почти не имеют зрения и ориентируются по запаху, оставленному предшественниками. Сильно пахнущее вещество, феромон, является для них индикатором деятельности предшественников. Оно аккумулирует в себе предысторию поиска и подсказывает дорогу к муравейнику. Попытки подглядеть у природы способы решения трудных комбинаторных задач находят все новые и новые воплощения в численных методах. Например, при инфекции организм старается подобрать (породить, сконструировать) наиболее эффективную защиту. Наблюдение за этим процессом привело к рождению нового метода – искусственным иммунным системам. Исследование жизнедеятельности пчелиного улья, где только одна матка оставляет потомство, послужило основой для новых генетических методов. Однако наибольший прогресс наблюдается на пути гибридизации, например, построения гиперэвристик, автоматически подбирающих наиболее эффективные эвристики для данного примера и симбиоз с классическими методами математического программирования.
Остановимся подробнее на последнем направлении. Здесь наблюдается достаточно широкий спектр исследований [24]:
– построение экспоненциальных по мощности окрестностей,
в которых поиск наилучшего решения осуществляется за полиномиальное время путем решения вспомогательной оптимизационной задачи;
– исследование операторов скрещивания, базирующихся на точ-ном или приближенном решении исходной задачи на подмножестве, заданном родительскими решениями;
– гибридизация метаэвристик с точными методами, например, с методами ветвей и границ и методом динамического программирования;
– разработка новых точных методов, использующих идеи локального поиска;
– применение разных математических формулировок решаемой задачи и использование различных кодировок решений и др.
Обзор достижений в данном направлении можно найти в [31]. Ниже будут представлены пять метаэвристик, четыре из которых являются траекторными алгоритмами. Каждая из них имеет свою идею и механизм ее реализации. Несмотря на то, что эта глава посвящена задаче коммивояжера, читатель легко увидит способы адаптации данных алгоритмов к другим задачам.
Алгоритм имитации отжига
Экзотическое название данного алгоритма связано с методами имитационного моделирования в статистической физике, основанными на технике Монте-Карло. Исследование кристаллической решетки и поведения атомов при медленном остывании тела привело к появлению на свет стохастических алгоритмов, которые оказались чрезвычайно эффективными в комбинаторной оптимизации. Впервые это было замечено в 1983 г. [32]. В настоящее время этот подход является популярным как среди практиков, благодаря своей простоте, гибкости и эффективности, так и среди теоретиков, поскольку для него удается доказать асимптотическую сходимость к глобальному оптимуму.
Алгоритм имитации отжига относится к классу пороговых алгоритмов локального поиска. На каждом шаге в окрестности текущего решения выбирается новое решение. Если разность по целевой функции между ними не превосходит заданного порога 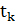 , то новое решение заменяет текущее. В противном случае выбирается другое соседнее решение. Общая схема пороговых алгоритмов может быть представлена следующим образом.
, то новое решение заменяет текущее. В противном случае выбирается другое соседнее решение. Общая схема пороговых алгоритмов может быть представлена следующим образом.
Пороговый алгоритм
1. Выбрать начальное решение 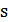 и положить
и положить 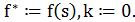
2. Пока не выполнен критерий остановки, делать следующее:
2.1. Выбрать 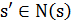 случайным образом.
случайным образом.
2.2. Если 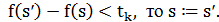
2.3. Если 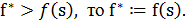
2.4. Положить 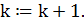
3. Предъявить наилучшее найденное решение.
В зависимости от способа задания последовательности 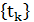 различают три типа алгоритмов
различают три типа алгоритмов
1. Последовательное улучшение: 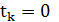 для всех
для всех 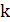 – вариант классического локального спуска с монотонным улучшением по целевой функции.
– вариант классического локального спуска с монотонным улучшением по целевой функции.
2. Пороговое улучшение: 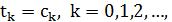
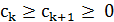
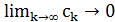 – вариант локального поиска, когда допускается ухудшение по целевой функции до некоторого порога, и этот порог последовательно снижается до нуля.
– вариант локального поиска, когда допускается ухудшение по целевой функции до некоторого порога, и этот порог последовательно снижается до нуля.
3. Имитация отжига: 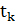 – неотрицательная случайная величина с математическим ожиданием
– неотрицательная случайная величина с математическим ожиданием 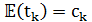 – вариант локального поиска, когда допускается произвольное ухудшение по целевой функции, но вероятность такого перехода обратно пропорциональна величине ухудшения, точнее для любого
– вариант локального поиска, когда допускается произвольное ухудшение по целевой функции, но вероятность такого перехода обратно пропорциональна величине ухудшения, точнее для любого 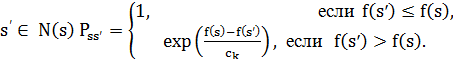
Последовательность 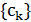 играет важную роль при анализе сходимости и выбирается так, чтобы
играет важную роль при анализе сходимости и выбирается так, чтобы 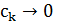 при
при 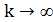 . Иногда параметр
. Иногда параметр 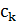 называют температурой, имея в виду указанные выше истоки. Для анализа данного и последующих алгоритмов потребуются некоторые определения из теории конечных цепей Маркова [32, 33].
называют температурой, имея в виду указанные выше истоки. Для анализа данного и последующих алгоритмов потребуются некоторые определения из теории конечных цепей Маркова [32, 33].
Определение 5.6. Пусть 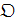 обозначает множество возможных исходов некоторого случайного процесса. Цепь Маркова есть последовательность испытаний, когда вероятность исхода в каждом испытании зависит только от результата предшествующего испытания.
обозначает множество возможных исходов некоторого случайного процесса. Цепь Маркова есть последовательность испытаний, когда вероятность исхода в каждом испытании зависит только от результата предшествующего испытания.
Пусть 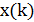 – случайная переменная, обозначающая результат
– случайная переменная, обозначающая результат
k-го испытания. Тогда для каждой пары 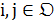 вероятность перехода от
вероятность перехода от 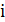 к
к 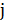 при k-ом испытании задается выражением
при k-ом испытании задается выражением 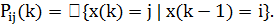
Матрица 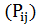 называется переходной матрицей. Цепь Маркова называется конечной, если множество исходов конечно, и однородной, если переходные вероятности не зависят от номера шага
называется переходной матрицей. Цепь Маркова называется конечной, если множество исходов конечно, и однородной, если переходные вероятности не зависят от номера шага 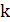 .
.
Для алгоритма имитации отжига испытание состоит в выборе очередного решения на k-м шаге. Вероятность перехода  зависит от текущего решения
зависит от текущего решения 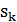 , так как переход возможен только в соседнее решение
, так как переход возможен только в соседнее решение  Она не зависит от того, каким путем добрались до этого решения. Таким образом, последовательность решений
Она не зависит от того, каким путем добрались до этого решения. Таким образом, последовательность решений 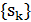 образует цепь Маркова. Эта цепь конечна, т. к. множество допустимых решений конечно. Для каждой пары
образует цепь Маркова. Эта цепь конечна, т. к. множество допустимых решений конечно. Для каждой пары 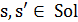 вероятность перехода от
вероятность перехода от 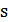 к
к 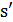 задается выражением:
задается выражением: 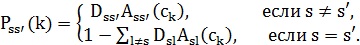
где 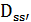 есть вероятность выбора решения
есть вероятность выбора решения 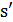 из окрестности
из окрестности 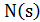 ,
, 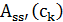 – вероятность принятия решения
– вероятность принятия решения 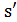 . Если в окрестности
. Если в окрестности  решения выбираются равновероятно, то
решения выбираются равновероятно, то 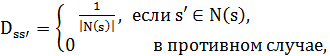 а вероятность принятия
а вероятность принятия 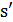 определяется как
определяется как 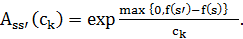
Если 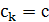 , то цепь Маркова является однородной. В общем случае алгоритм имитации отжига порождает конечную неоднородную цепь Маркова.
, то цепь Маркова является однородной. В общем случае алгоритм имитации отжига порождает конечную неоднородную цепь Маркова.  При исследовании асимптотического поведения алгоритмов важную роль играет так называемое стационарное распределение, вектор
При исследовании асимптотического поведения алгоритмов важную роль играет так называемое стационарное распределение, вектор 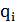 размерности
размерности 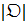 , компоненты которого определяются как
, компоненты которого определяются как 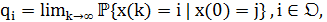 если такой предел существует и не зависит от
если такой предел существует и не зависит от 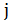 . Величина
. Величина 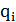 равна вероятности оказаться в состоянии
равна вероятности оказаться в состоянии 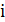 после достаточно большого числа шагов.
после достаточно большого числа шагов.
Теорема 5.14. Пусть 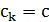 для всех
для всех 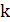 и для любой пары
и для любой пары 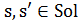 найдутся положительное целое число
найдутся положительное целое число 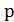 и такие решения
и такие решения 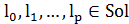 , что
, что 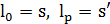 и
и 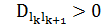 для
для 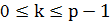 . Тогда для цепи Маркова, порожденной алгоритмом имитации отжига, существует единственное стационарное распределение, компоненты которого задаются формулой
. Тогда для цепи Маркова, порожденной алгоритмом имитации отжига, существует единственное стационарное распределение, компоненты которого задаются формулой
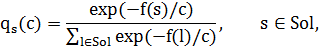
и
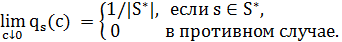
Последнее равенство, по сути, означает, что с ростом числа итераций вероятность оказаться в точке глобального оптимума стремится к 1, если значение порога 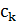 стремится к нулю, то есть
стремится к нулю, то есть 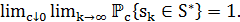
На практике, конечно, нет возможности выполнить бесконечное число итераций. Поэтому приведенная теорема является только источником вдохновения при разработке алгоритмов. Существует много эвристических способов выбора конечной последовательности 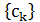 с целью повышения вероятности обнаружения глобального оптимума.
с целью повышения вероятности обнаружения глобального оптимума.
В большинстве работ следуют рекомендациям первопроходцев и используют схему геометрической прогрессии:
1. Начальное значение 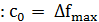 – максимальная разность между соседними решениями.
– максимальная разность между соседними решениями.
2. Понижение порога: 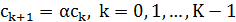 , где
, где 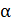 – положительная константа, достаточно близкая к 1.
– положительная константа, достаточно близкая к 1.
3. Финальное значение: 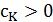 определяется либо по числу сделанных изменений, либо как максимальное
определяется либо по числу сделанных изменений, либо как максимальное 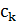 , при котором алгоритм не меняет текущее решение в течение заданного числа шагов. При каждом значении
, при котором алгоритм не меняет текущее решение в течение заданного числа шагов. При каждом значении 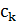 алгоритм выполняет порядка
алгоритм выполняет порядка 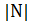 шагов, не меняя значение порога. Общая схема имитации отжига может быть представлена следующим образом.
шагов, не меняя значение порога. Общая схема имитации отжига может быть представлена следующим образом.
Алгоритм SA
1. Выбрать начальное решение 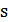 и положить
и положить 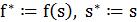 , определить начальную температуру
, определить начальную температуру 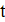 и коэффициент
и коэффициент 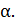
2. Повторять, пока не выполнен критерий остановки.
2.1. Цикл 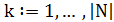 .
.
Выбрать решение 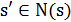 случайным образом.
случайным образом.
Вычислить 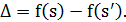
Если 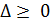 , то
, то 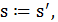 иначе
иначе 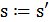 с вероятностью
с вероятностью 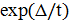 .
.
Если 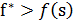 , то
, то 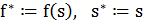 .
.
2.2. Понизить температуру: 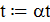 .
.
3. Предъявить наилучшее найденное решение 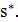
На рис. 5.20 показано типичное поведение алгоритма. На первых итерациях при высокой температуре наблюдается большой разброс по целевой функции. Процесс поиска чем-то напоминает броуновское движение.
| Итерации |
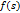 |
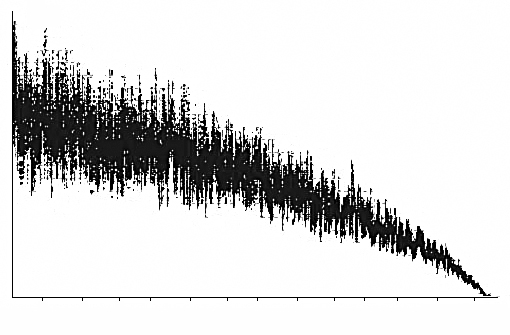
Рисунок-5.20. Поведение алгоритма SA
По мере понижения температуры разброс уменьшается, и наблюдается явная тенденция к падению среднего значения целевой функции. При низкой температуре наблюдается стагнация процесса. Все чаще и чаще не удается перейти в соседнее решение, и алгоритм останавливается в одном из локальных оптимумов.
Среди пороговых алгоритмов следует выделить еще один с забавным названием великий потоп (Great Deluge). Правда, для задач на минимум его следует называть скорее великая засуха. На каждой итерации этого алгоритма имеется некоторое допустимое решение задачи  , и в его окрестности, как и раньше, выбирается решение
, и в его окрестности, как и раньше, выбирается решение 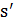 случайным образом. Если
случайным образом. Если 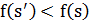 , то выполняется переход в новое решение. В противном случае значение
, то выполняется переход в новое решение. В противном случае значение 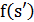 сравнивается с уровнем воды
сравнивается с уровнем воды 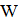 . Если
. Если 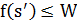 , то все равно выполняется переход в новое решение. Если же переход не выполнен, то выбирается новое соседнее решение. Порог
, то все равно выполняется переход в новое решение. Если же переход не выполнен, то выбирается новое соседнее решение. Порог 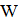 сначала устанавливается достаточно большим, чтобы были возможны любые переходы. Затем этот порог уменьшается на каждой итерации на заданную величину
сначала устанавливается достаточно большим, чтобы были возможны любые переходы. Затем этот порог уменьшается на каждой итерации на заданную величину 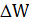 . Процесс останавливается в локальном минимуме со значением выше уровня воды. Общая схема алгоритма не сильно отличается от имитации отжига, но приводит к качественно другой картине.
. Процесс останавливается в локальном минимуме со значением выше уровня воды. Общая схема алгоритма не сильно отличается от имитации отжига, но приводит к качественно другой картине.
Алгоритм GD
1. Выбрать начальное решение 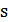 и положить
и положить 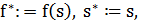 определить начальный порог
определить начальный порог 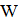 и скорость его падения
и скорость его падения 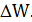
2. Повторять, пока не выполнен критерий остановки.
2.1. Выбрать решение 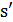 Î
Î 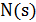 случайным образом.
случайным образом.
2.2. Вычислить 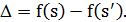
2.3. Если 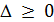 , то
, то 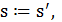 иначе если
иначе если 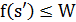 , то
, то 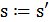 .
.
2.4. Если 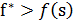 , то
, то 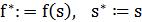 .
.
2.5. Понизить порог: 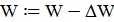 .
.
3. Предъявить наилучшее найденное решение 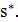
На рис. 5.21 показано типичное поведение алгоритма. Падение порога на каждой итерации вынуждает искать направления спуска. Как рыба, которая не хочет оказаться на суше, мы ищем все более и более глубокие места. Заметим, что для реализации алгоритма достаточно уметь вычислять значение целевой функции и определять окрестность. Параметры 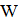 и
и 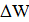 легко настраиваются под специфику задачи, что открывает широкий простор для приложений.
легко настраиваются под специфику задачи, что открывает широкий простор для приложений.
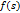 |
| Итерации |
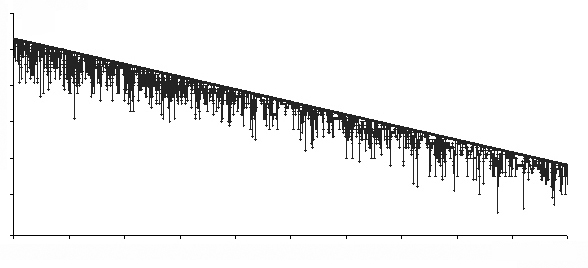
Рисунок-5.21. Поведение алгоритма GD
Поиск с запретами
Основоположником алгоритма поиска с запретами является Ф. Гловер, который в 1986 г. предложил принципиально новую схему локального поиска [34]. Она позволяет алгоритму не останавливаться в точке локального оптимума, как это предписано в стандартном алгоритме локального улучшения, а путешествовать от одного оптимума к другому, в надежде найти среди них глобальный оптимум. Основным механизмом, позволяющим алгоритму выбираться из локального оптимума, является список запретов 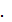 Он строится по предыстории поиска, то есть по нескольким последним решениям,
Он строится по предыстории поиска, то есть по нескольким последним решениям,  и запрещает часть окрестности текущего решения
и запрещает часть окрестности текущего решения 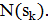 Точнее, на каждом шаге алгоритма новое решение
Точнее, на каждом шаге алгоритма новое решение 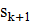 является оптимальным решением подзадачи
является оптимальным решением подзадачи 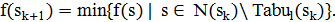
Список запретов учитывает специфику задачи и, как правило, запрещает использование тех «фрагментов» решения (ребер графа, координат вектора, цвета вершин), которые менялись на последних 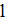 шагах алгоритма. Константа
шагах алгоритма. Константа 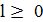 определяет его память. При «короткой памяти»
определяет его память. При «короткой памяти» 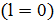 получаем стандартный алгоритм локального улучшения.
получаем стандартный алгоритм локального улучшения.
Существует много вариантов реализации этой идеи. Приведем один из них, для которого удается установить асимптотические свойства. Рассмотрим рандомизированную окрестность 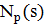 . Каждый элемент окрестности
. Каждый элемент окрестности 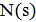 включается в множество
включается в множество 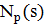 с вероятностью
с вероятностью  независимо от других элементов. С ненулевой вероятностью множество
независимо от других элементов. С ненулевой вероятностью множество 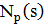 может совпадать с
может совпадать с 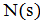 , может оказаться пустым или содержать ровно один элемент. Общая схема алгоритма поиска с запретами может быть представлена следующим образом.
, может оказаться пустым или содержать ровно один элемент. Общая схема алгоритма поиска с запретами может быть представлена следующим образом.
Алгоритм TS
1. Выбрать начальное решение  и положить
и положить 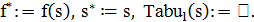
2. Повторять, пока не выполнен критерий остановки.
2.1. Сформировать окрестность 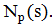
2.2. Если 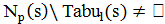 , то найти такое решение
, то найти такое решение 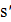 , что
, что 
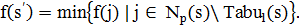
2.3. Если 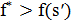 , то
, то 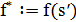 и
и 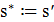 .
.
2.4. Положить 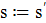 и обновить список запретов.
и обновить список запретов.
3. Предъявить наилучшее найденное решение 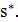
Параметры  и
и 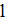 являются управляющими для данного алгоритма. Выбор их значений зависит от размерности задачи и мощности окрестности. Примеры адаптации этой схемы к разным задачам комбинаторной оптимизации можно найти, например, в [23].
являются управляющими для данного алгоритма. Выбор их значений зависит от размерности задачи и мощности окрестности. Примеры адаптации этой схемы к разным задачам комбинаторной оптимизации можно найти, например, в [23].
Пусть 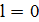 . Тогда алгоритм TS порождает конечную однородную цепь Маркова. Можно показать, что в этом случае переходные вероятности
. Тогда алгоритм TS порождает конечную однородную цепь Маркова. Можно показать, что в этом случае переходные вероятности 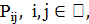 определяются равенством
определяются равенством 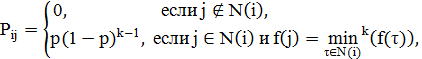 где
где 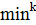 означает k-й минимальный элемент множества. Если граф окрестностей
означает k-й минимальный элемент множества. Если граф окрестностей 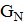 строго связен, то для такой цепи Маркова существует единственное стационарное распределение, и вероятность не найти глобальный оптимум стремится к нулю со скоростью геометрической прогрессии. Заметим, что для стационарного распределения не получено точной формулы, как это удалось сделать для алгоритма имитации отжига. Утверждается только существование и единственность такого распределения. При малых размерностях его можно получить численно из соотношений
строго связен, то для такой цепи Маркова существует единственное стационарное распределение, и вероятность не найти глобальный оптимум стремится к нулю со скоростью геометрической прогрессии. Заметим, что для стационарного распределения не получено точной формулы, как это удалось сделать для алгоритма имитации отжига. Утверждается только существование и единственность такого распределения. При малых размерностях его можно получить численно из соотношений 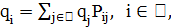
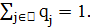
Аналитического выражения для решения такой системы не известно. Тем не менее, исследование этого распределения и, в частности, его компонент, соответствующих глобальному оптимуму, представляет несомненный интерес.
Пусть 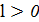 . В этом случае последовательность решений уже не является цепью Маркова, т. к. выбор следующего решения зависит от предыстории. Однако, если рассмотреть множество кортежей
. В этом случае последовательность решений уже не является цепью Маркова, т. к. выбор следующего решения зависит от предыстории. Однако, если рассмотреть множество кортежей  длины
длины 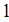 , то такая последовательность, порождаемая алгоритмом, уже будет конечной однородной цепью Маркова. Матрица переходных вероятностей имеет теперь значительно большую размерность, но ее элементы будут определяться по сути теми же формулами, что и раньше.
, то такая последовательность, порождаемая алгоритмом, уже будет конечной однородной цепью Маркова. Матрица переходных вероятностей имеет теперь значительно большую размерность, но ее элементы будут определяться по сути теми же формулами, что и раньше.
Список запретов оказывает существенное влияние на поведение алгоритма. В частности, если на некотором шаге все соседние решения оказываются под запретом, то процесс поиска прекращается. Таким образом, даже свойство строгой связности графа 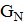 не гарантирует желаемого асимптотического поведения. Тем не менее, при определенных условиях на длину этого списка удается обеспечить сходимость по вероятности наилучшего найденного решения к глобальному оптимуму.
не гарантирует желаемого асимптотического поведения. Тем не менее, при определенных условиях на длину этого списка удается обеспечить сходимость по вероятности наилучшего найденного решения к глобальному оптимуму.
На рис. 5.22 показано типичное поведение алгоритма TS. На первых итерациях он ведет себя как стандартный алгоритм локального улучшения. Получив первый локальный минимум, алгоритм вынужден выполнить несколько шагов с ухудшением, после чего снова открывается путь к новым локальным оптимумам. Рандомизация окрестности привносит определенное разнообразие в процесс поиска и предотвращает зацикливание. Более того, она позволяет сократить трудоемкость одного шага алгоритма и часто повышает вероятность нахождения глобального оптимума за предписанное число итераций. Чем сложнее и запутаннее пример, тем меньшую долю окрестности следует просматривать. Как правило, значения параметра 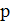 в интервале от 0.2 до 0.3 приводят к хорошим результатам даже при небольшом числе итераций.
в интервале от 0.2 до 0.3 приводят к хорошим результатам даже при небольшом числе итераций.
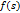 |
| Итерации |
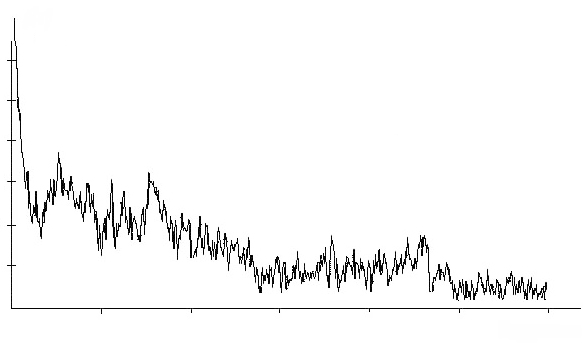
Рисунок-5.22. Поведение алгоритма TS
