Окрестности на перестановках
Как уже отмечалось выше, выбор окрестности играет важную роль при построении алгоритмов локального поиска. От него существенно зависит трудоемкость одного шага алгоритма, общее число шагов и, в конечном счете, качество получаемого локального оптимума. На сегодняшний день нет (и, возможно, никогда не будет) единого правила выбора окрестности. Для каждой задачи функцию  приходится определять заново, учитывая специфику данной задачи. Более того, по-видимому для каждой задачи можно предложить несколько функций окрестности с разными по мощности множествами соседей и, как следствие, разными множествами локальных оптимумов. Ниже будут приведены три примера выбора окрестностей для задачи коммивояжера, которые иллюстрируют возможные пути построения окрестностей и их свойства.
приходится определять заново, учитывая специфику данной задачи. Более того, по-видимому для каждой задачи можно предложить несколько функций окрестности с разными по мощности множествами соседей и, как следствие, разными множествами локальных оптимумов. Ниже будут приведены три примера выбора окрестностей для задачи коммивояжера, которые иллюстрируют возможные пути построения окрестностей и их свойства.
Будем по-прежнему рассматривать задачу коммивояжера с симметричной матрицей расстояний и гамильтонов цикл представлять в виде перестановки  . Определим окрестность
. Определим окрестность  как множество всех перестановок, отличающихся от
как множество всех перестановок, отличающихся от  только в двух позициях (
только в двух позициях (  -
-  ). Множество
). Множество  содержит ровно
содержит ровно  элементов, и вычислительная сложность одного шага локального поиска с учетом вычисления целевой функции не превосходит
элементов, и вычислительная сложность одного шага локального поиска с учетом вычисления целевой функции не превосходит 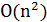 операций.
операций.
Обозначим через  длину гамильтонова цикла и определим разностный оператор
длину гамильтонова цикла и определим разностный оператор  для
для  следующим образом [26]:
следующим образом [26]: 
Этот оператор задает среднее отклонение целевой функции в окрестности данной перестановки. Для локального оптимума  справедливо неравенство
справедливо неравенство  . Пусть
. Пусть  – средняя длина цикла на множестве всех допустимых решений задачи. Тогда справедливы следующие утверждения.
– средняя длина цикла на множестве всех допустимых решений задачи. Тогда справедливы следующие утверждения.
Теорема 5.10. Функция  удовлетворяет уравнению
удовлетворяет уравнению
 .
.
Следствие 5.1. Любой локальный минимум  имеет длину
имеет длину 
Следствие 5.2. Алгоритм локального поиска, начиная с произвольной перестановки, достигнет локального оптимума за  шагов, если длина максимального тура превосходит среднее значение
шагов, если длина максимального тура превосходит среднее значение  не более чем в
не более чем в  раз.
раз.
Аналогичные утверждения справедливы и для следующих задач:
1) о разбиении  -вершиного графа на две части по
-вершиного графа на две части по  вершин с минимальным суммарным весом ребер, соединяющих эти части;
вершин с минимальным суммарным весом ребер, соединяющих эти части;
2) о раскраске вершин графа в  цветов так, чтобы смежные вершины имели разные цвета;
цветов так, чтобы смежные вершины имели разные цвета;
3) о разбиении n-элементного множества на два подмножества так, чтобы суммарный вес одного подмножества совпал с суммарным весом другого подмножества;
4) о 3-выполнимости в следующей постановке: для  булевых переменных задан набор троек; каждая переменная может входить в набор с отрицанием или без него; набор считается выполненным, если он содержит разные значения, то есть хотя бы одно истинное и хотя бы одно ложное; требуется узнать, существует ли назначение переменных, при котором все наборы будут выполнены. Развитие этих идей можно найти в [27].
булевых переменных задан набор троек; каждая переменная может входить в набор с отрицанием или без него; набор считается выполненным, если он содержит разные значения, то есть хотя бы одно истинное и хотя бы одно ложное; требуется узнать, существует ли назначение переменных, при котором все наборы будут выполнены. Развитие этих идей можно найти в [27].
