Решение задач линейного программирования методом искусственного базиса

Метод искусственного базиса (или метод “М”) может быть применен для решения задачи ЛП, если ее система ограничений, помимо неравенств смысла “≤” имеет неравенства смысла “≥” или строгие равенства. Рассмотрим задачу ЛП, заданную в самом общем виде.

Найти экстремум функции

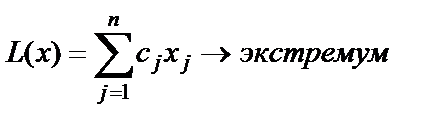(1.26)

при следующих ограничениях:

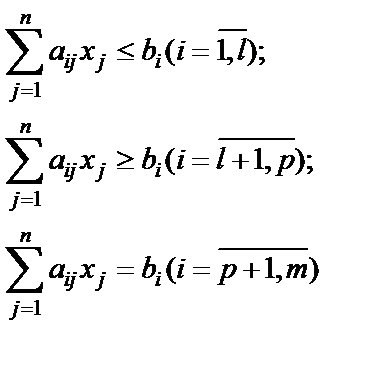	(1.27)
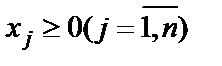	(1.28)

Алгоритм метода «М».

1. От системы неравенств переходим к системе уравнений, вводя дополнительные неотрицательные переменные: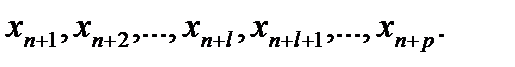

2. В ограничения, в которые дополнительные неотрицательные переменные вошли со знаком минус или вообще не вошли, вводятся так называемые искусственные переменные: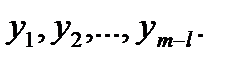

3. В линейную форму (1.26) вводится сумма искусственных переменных 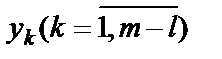с коэффициентом M>0. Для того, чтобы искусственные переменные не содержались в оптимальном плане исходной задачи, коэффициенту М придается произвольно большое значение по сравнению с коэффициентами 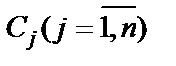линейной формы (1.26). В этом случае при максимизации функции цели (1.26), берем (-М), при минимизации (+М).

4. Строим расширенную М – задачу ЛП:

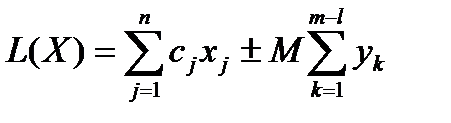
найти экстремум линейной формы

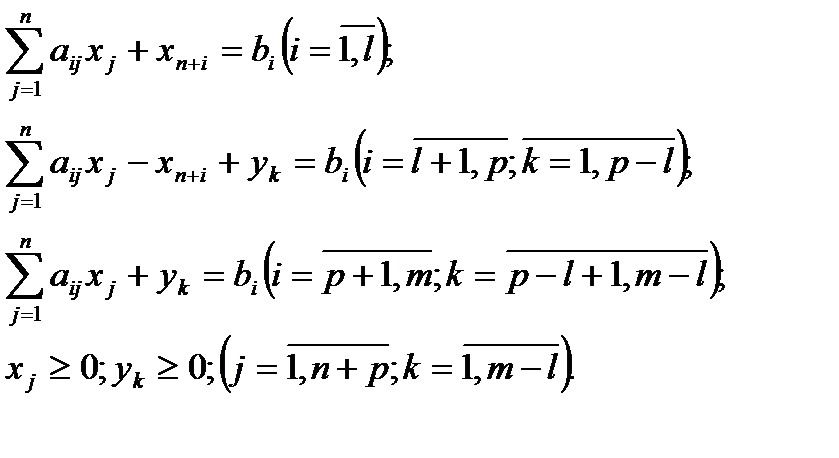
при следующих ограничениях:

Найдем первоначальный опорный план М – задачи.

Так как дополнительные неотрицательные переменные 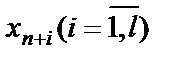и искусственные переменные 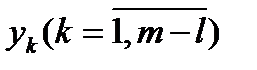входят в ограничения с положительными единичными коэффициентами, которые составляют систему линейно-независимых векторов как столбцы единичной матрицы, то упомянутые переменные будут являться базисными, а все остальные – свободными, т.е.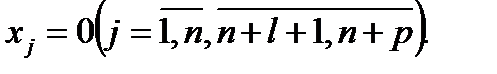

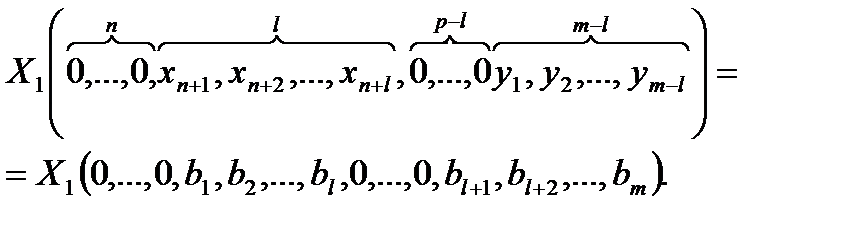
Тогда первоначальный опорный план будет иметь вид:

6. Для отыскания оптимального плана расширенной М – задачи составляют симплекс-таблицу, которая на одну строку больше, чем обычная. В эту (m+2) индексную строку записываются соответствующий коэффициенты при М, входящими в целевую функцию с противоположным знаком.

Проверяется признак оптимальности по (m+2)-й строке и определяется переменная, подлежащая включению в базис. Симплекс-процедуру по (m+2) индексной строке проводят до тех пор, пока по этой строке не будет выполнен признак оптимальности. Затем процесс отыскания оптимального плана продолжают по (m+1) индексной строке.

7. Анализируем оптимальный план М – задачи. Если в этом плане все искусственные переменные равны нулю, т.е. 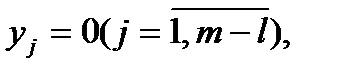то план X(x₁, x₂, …, x_n) является оптимальным планом исходной задачи. Если же в оптимальном плане М – задачи хотя бы одна искусственная переменная не равна нулю, т.е. 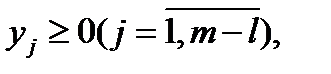то исходная задача решения не имеет.

Если в процессе решения М – задачи устанавливаем ее не разрешимость, то неразрешима и исходная задача.

Решение контрольного примера.

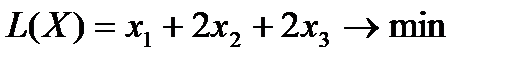
Найти минимум функции

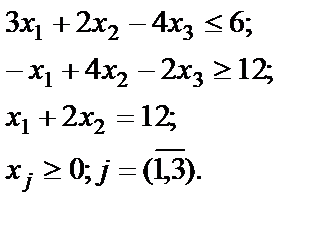
при следующих ограничениях:

1. От системы неравенств переходим к системе уравнений, вводя в 1-е и во 2-е ограничения дополнительные неотрицательные переменные x₄ и x₅. Третье уравнение переписываем без изменения:

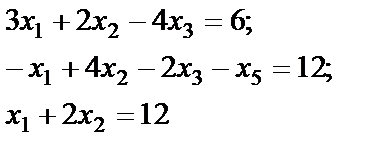2. Во 2-е и 3-е уравнения вводим искусственные переменные y₁ и y₂:

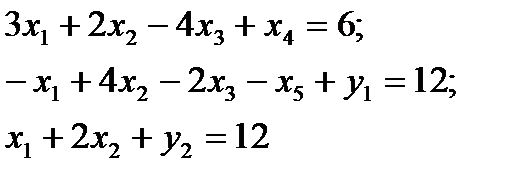
3. В линейную форму L(X) вводим сумму y₁+y₂ с множителем М. Так как задача поставлена на минимум, то множитель М берем со знаком «+».

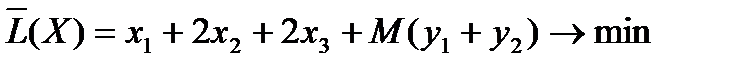
4. Строим М – задачу. Найти минимум линейной формы

при следующих ограничениях:

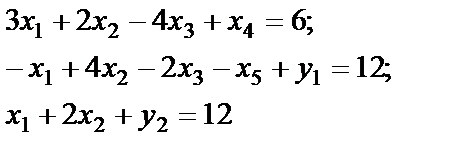
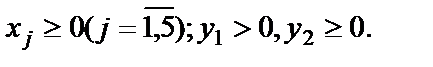
5. Решаем эту задачу симплекс-методом. Так как x₄, y₁, y₂ являются базисными переменными, то выражаем их через свободные и подставляем в функцию L(X):

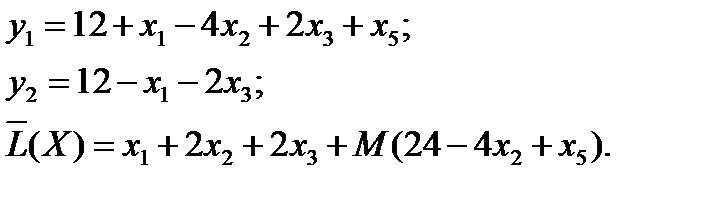
6. Строим симплекс-таблицу, которая имеет две индексные строки: в первую, как обычно, записываются коэффициенты Cj, взятые с противоположным знаком, а во вторую – соответствующие коэффициенты при множителе М (тоже с обратным знаком, кроме свободного члена).

Проверяем признак оптимальности по (m+2) индексной строке. Так как задача на минимум, то признак не выполнен, поскольку в столбце x₂ находится положительный элемент 4. Отмечаем этот ключевой столбец стрелкой и, как обычно, выбираем ключевую строку. При выборе ключевой строки получили два одинаковых наименьших значения θ. Чтобы избежать зацикливания, применяем правило Креко. Строки x₁ и y₁ делим на соответствующие элементы ключевого столбца 2 и 4. Результаты от деления читаем слева направо, и ту строку, где первым встретится меньшее число, выбираем за ключевую, т.е.

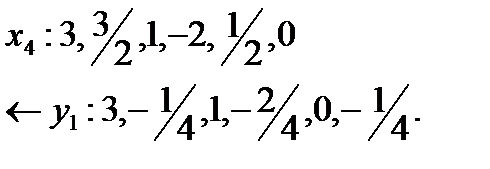
Отмечаем строку y₁ стрелкой и находим генеральный элемент 4. Затем выполняем обычную симплекс-процедуру и получаем вторую таблицу (таблица 1.2.), в которой опять анализируем (m+2)-ю индексную строку и выбираем столбец x₃ за ключевой.

В результате построения третьей таблицы (таблица 1.2.) получаем оптимальный план расширенной задачи 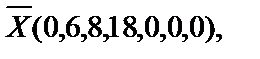так как по обеим индексным строкам признак оптимальности выполнен.

Вследствие того, что все искусственные переменные выведены из базиса, оптимальным планом исходной задачи является план 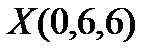и

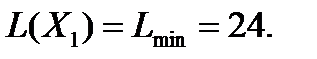
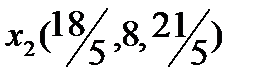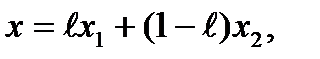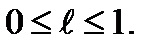Для рассматриваемой задачи можно построить второе оптимальное решение с тем же самым значением L_min=24 (таблица 1.2.). Следовательно, задача имеет множество оптимальных планов где [2]

Таблица 1.2.

№ таблиц	Базисные переменные	Свободные члены	X1	X2	X3	X4	X5	å	Q
	X4				-4
Y1		-1		-2		-1
Y2								-
L(X)		-1	-2	-2			-5	Min
		4­			-1		-
	X4		7/2		-3		1/2		-
X2		-1/4		-1/4		-1/4		-
Y2
L(X)		-3/2		-3		-1/2		Min
			2­
	X3		1/2					15/2
X2						-1/4	27/4	-
X4						1/2	49/2	18/5
L(X)						-1/2	47/2	Min
	X3	21/5			-1/10		-1/20	101/20
X2						-1/4	27/4
X4	18/5			1/5		-1/10	49/10
L(X)						-1/2	47/2	min