Тема 3. Линейный регрессионный анализ

Линейные регрессионные модели

БЛОК 1

1. В линейной регрессионной модели 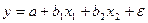ненаблюдаемой величиной является

○ y,

○ ,

○ ,

○ .

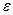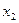2. В линейном уравнении множественной регрессии 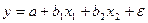метод наименьших квадратов не позволяет оценить значение …

○ ,

○ ,

○ ,

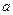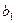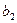○ y.

3. Предположим, что переменная y связана с k независимыми переменными 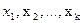линейной зависимостью 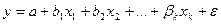. Оценка этого уравнения для заданного множества наблюдений n методом наименьших квадратов (МНК) имеет вид: 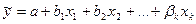. Тогда смысл коэффициентов 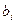состоит в том, что …………… при прочих равных условиях.

○ если 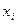изменится на одну единицу, то y изменится на (- 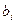) единиц,

○ если 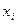изменится на одну единицу, то y изменится на %,

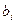○ если 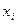изменится на одну единицу, то y изменится на 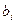единиц,

○ если 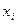изменится на одну единицу, то y изменится в 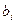раз.

4. Требованием к уравнениям регрессии, параметры которых можно найти при помощи МНК, является ….

○ равенство нулю средних значений результативной переменной,

○ нелинейность параметров,

○ линейность параметров,

○ равенство нулю средних значений факторного признака.

5. Пусть наблюдаемые значения зависимой переменной отличаются от модельных на величину 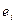. В данных обозначениях оценки коэффициентов регрессии по МНК определяются из условия минимизации суммы:

○ ,

○ ,

○ ,

○ .

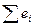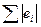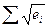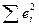6. Пусть 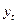– фактические значения, 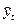– расчетные значения, 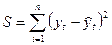, тогда система нормальных уравнений получается из условия …

○ равенства значения функции S нулю,

○ минимизации функции S,

○ максимизации функции S,

○ равенства значения функции S единице.

7. Построена парная модель линейной регрессии 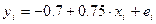, , 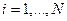и рассчитан коэффициент парной линейной корреляции 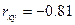. Такие результаты невозможны, так как …

○ коэффициент регрессии по модулю меньше коэффициента корреляции,

○ коэффициент регрессии и коэффициент корреляции имеют разные знаки,

○ свободный член регрессии и коэффициент корреляции имеют одинаковые знаки,

○ свободный член регрессии больше коэффициента корреляции.

8. В эконометрических моделях «объясненная» дисперсия – это дисперсия…

○ случайных отклонений,

○ наблюдаемых значений результативного фактора,

○ расчетных значений результативного фактора,

○ значений объясняющего фактора.

9. Остаток регрессионной модели представляет собой оценку …

○ факторной переменной,

○ случайной ошибки,

○ коэффициента регрессии,

○ свободного члена.

10. Оценка удельного веса влияния каждой из объясняющих переменных на результирующий показатель является задачей …

○ кластерного анализа,

○ компонентного анализа,

○ метода наименьших квадратов,

○ регрессионного анализа.

11. Метод наименьших квадратов предназначен для оценки параметров линейной эконометрической модели на основании результатов наблюдений, содержащих …

○ систематические ошибки,

○ случайные ошибки,

○ ошибки измерения,

○ ошибки спецификации.

12. При построении модели множественной регрессии методом пошагового включения переменных на первом этапе рассматривается модель с …

○ одной объясняющей переменной, которая имеет с зависимой переменной наибольший коэффициент корреляции,

○ одной объясняющей переменной, которая имеет с зависимой переменной наименьший коэффициент корреляции,

○ несколькими объясняющими переменными, которые имеют с зависимой переменной коэффициенты корреляции по модулю больше 0,5,

○ полным перечнем объясняющих переменных.

13. Величина коэффициента регрессии показывает …

○ характер связи между фактором и результатом

○ среднее изменение результата при изменении фактора на одну единицу

○ тесноту связи между фактором и результатом

○ тесноту связи между исследуемыми факторами.

14. Свойства оценок параметров, получаемых при помощи метода наименьших квадратов, предполагают исследование _____ величин уравнения регрессии.

○ детерминированных

○ постоянных

○ независимых

○ остаточных.

15. Обобщенный метод наименьших квадратов может применяться в случае нарушения предпосылки МНК о _______ остатков.

○ гомоскедастичности

○ количественной измеримости

○ минимизации

○ нормальном распределении.

16. Пусть исследуется линейная зависимость вида 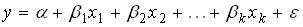и оценена регрессия 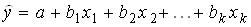, 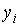– фактические значения, а 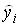– расчетные значения зависимой переменной, 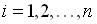. Тогда общую дисперсию можно оценить по формуле …

○

○

○

○ .

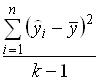
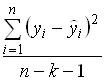
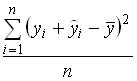
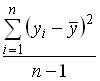17. Число степеней свободы связано …

○ только с видом уравнения регрессии

○ с числом единиц совокупности и видом уравнения регрессии

○ характером исследуемых переменных

○ только с числом единиц совокупности.

18. Использование в эконометрическом моделировании парной регрессии вместо множественной является ошибкой ...

○ выборки

○ линеаризации

○ измерения

○ спецификации.

19. Для уравнения множественной регрессии 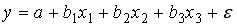построено частное уравнение вида 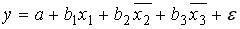, в котором х₂ и х₃ …

○ являются изменяемыми факторными переменными

○ не оказывают существенное влияние на у

○ приравнены к 1

○ закреплены на неизменном среднем уровне.

20. Метод наименьших квадратов применим к уравнениям регрессии …

○ которые отражают нелинейную зависимость между двумя экономическими показателями и не могут быть приведены к линейному виду

○ нелинейного вида

○ которые отражают нелинейную зависимость между двумя экономическими показателями, но могут быть приведены к линейному виду

○ которые отражают линейную зависимость между двумя экономическими показателями.

21. Если предпосылки метода наименьших квадратов нарушены, то …

○ оценки параметров могут не обладать свойствами эффективности,

состоятельности и несмещенности

○ коэффициент корреляции является несущественным

○ коэффициент регрессии является несущественным

○ полученное уравнение статистически незначимо.

22. Обобщенный МНК применяется в случае…

○ наличия в остатках гетероскедастичности или автокорреляции

○ наличия в модели мультиколлинеарности

○ наличия в модели фиктивных переменных

○ наличия в модели незначимых оценок.

23. Метод наименьших квадратов используется для оценивания …

○ величины коэффициента корреляции

○ средней ошибки аппроксимации

○ величины коэффициента детерминации

○ параметров линейной регрессии.

24. Суть метода наименьших квадратов (МНК) состоит …

○ в минимизации суммы квадратов отклонений фактического значения зависимой переменной от ее расчетного (моделируемого) значения

○ в максимизации суммы квадратов отклонений фактического значения зависимой переменной от ее расчетного (моделируемого) значения,

○ в минимизации суммы отклонений фактического значения от расчетного

○ в максимизации абсолютных величин отклонений фактического значения от расчетного.

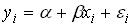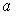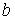25. При построении модели с помощью МНК, эмпирические оценки и параметров 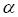и 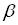будут находиться из условия…

○ минимизации величины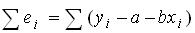

○ максимизации величины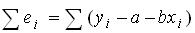

○ максимизации величины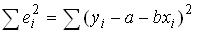

○ минимизации величины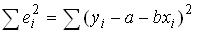

26. Метод наименьших квадратов предназначен для оценки параметров линейной эконометрической модели на основании результатов наблюдений, содержащих …

○ ошибки спецификации,

○ ошибки измерения,

○ случайные ошибки,

○ систематические ошибки.

27. Для приведения объясненной, общей и остаточной дисперсии к сравнимому виду вводят понятие …

○ дисперсии на одну степень свободы,

○ F-критерия Фишера,

○ универсальной дисперсии,

○ стандартного отклонения.

28. Диаграмма рассеивания между некоторыми переменными x и y имеет вид

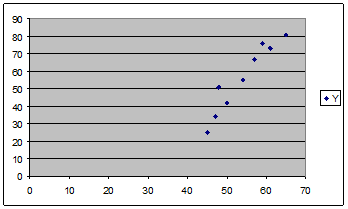
Тогда зависимость между переменными x и y …

○ близка к линейной ,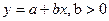

○ близка к квадратичной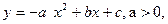

○ близка к квадратичной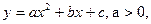

○ близка к линейной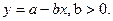

29. Пусть оценивается регрессия 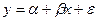. Известна оценка b параметра 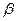, тогда оценка a параметра 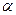может быть вычислена по формуле:

○

○

○

○ .

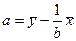
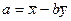
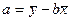
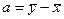БЛОК 2

1. Установите соответствие между экономическим смыслом и параметрами уравнений множественной регресси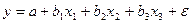и

и :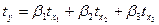

1. Среднее изменение у при изменении на одну единицу своего измерения при неизменном уровне других факторов.

2. На сколько среднеквадратических отклонений (СКО) изменится у при изменении на одно СКО.

3. Значение у при нулевых значениях , , 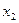при отсутствии влияния случайных факторов.

4. Среднее изменение у при изменении на одну единицу своего измерения при неизменном уровне других факторов.

2. □ ,

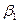1. □ ,

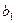3. □ a,

4. □ .

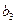2. Обобщенный метод наименьших квадратов подразумевает …

□ двухэтапное применение метода наименьших квадратов,

□ введение в выражение для дисперсии остатков коэффициента пропорциональности,

□ переход от множественной регрессии к парной,

□ преобразование переменных.

3. Установите соответствие между наименованиями уравнений множественной регрессии:

1) уравнение множественной регрессии в естественном масштабе,

2) стандартизированное уравнение множественной регрессии,

3) частное уравнение множественной регрессии с одной независимой переменной,

4) частное уравнение множественной регрессии с двумя независимыми переменными.

4. □ ,

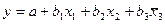3. □ ,

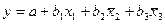1. □ ,

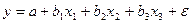2. □ .

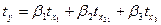4. В линейном уравнении парной регрессии 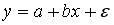переменными не являются …

□ y,

□ x,

□ a,

□ b.

5. Отбор факторов в модель множественной регрессии с использованием метода включения может быть основан на сравнении …

□ стандартных ошибок коэффициентов регрессии

□ величины объясненной дисперсии до и после включения фактора в модель

□ величины остаточной дисперсии до и после включения фактора в модель

□ значений коэффициентов "чистой" регрессии.

6. Для линейного уравнения регрессии 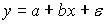метод наименьших квадратов используется при оценивании параметров…

□ a

□ y

□ b

□ x.

7. Предпосылками МНК являются:

□ дисперсия случайных отклонений постоянна для всех наблюдений

□ случайные отклонения являются независимыми друг от друга

□ случайные отклонения коррелируют друг с другом

□ гетероскедастичность случайных отклонений.

8. Установите соответствие между наименованиями элементов уравнения Y=b₀+b₁X+e и их буквенными обозначениями:

1. параметры регрессии
2. объясняющая переменная
3. объясняемая переменная
4. случайные отклонения

2. □ X

4. □ e

3. □ Y

1. □ b₀, b₁

9. Установите соответствие между наименованиями параметров и переменных уравнений множественной регрессии

:

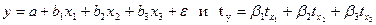1. коэффициенты «чистой» регрессии,

2. стандартизированные коэффициенты регрессии,

3. переменные в естественном масштабе,

4. стандартизированные переменные.

4. □ ,

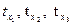1. □ ,

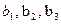2. □

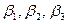
3. □ .

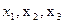10. Установите соответствие между наименованиями элементов уравнения 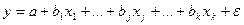и их буквенными обозначениями:

1. коэффициент «чистой» регрессии,

2. зависимая переменная,

3. независимая переменная,

4. влияние неучтенных явным образом в модели факторов.

2. □ y

1. □

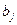
4. □

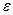
3. □ .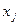