Перемещение поры как единого целого

Под влиянием силовых полей изолированная пора может перемещаться как целое макроскопическое включение вкристаллическом теле. Силовое поле может быть различным по происхождению. В частности, оно может определяться градиентом температуры, напряжений, электрического потенциала, концентрации диффундирующего компонента в диффузионной зоне. Оно может создаваться порой или дислокацией, находящимися в непосредственном соседстве, или границами зерен, примыкающими к поре.

Общеизвестным примером перемещения поры как целого является всплывание пузырька в воде под влиянием градиента потенциальной энергии в гравитационном поле. Заметим, что перемещение поры во внешнем силовом поле, вне зависимости от механизма, определяется принципом Ле-Шателье: перенос массы между различными участками поверхности поры есть следствие процессов, стремящихся вернуть систему в равновесие, из которого она постоянно выводится силовым полем.

Скорость перемещения, ее зависимость от линейного размера поры, в условиях изотермического опыта определяется механизмом переноса вещества между «передним» и «задним» участками поверхности поры в направлении, противоположном ее перемещению. В общем случае справедливо выражение

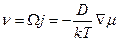_, (3.29)

где j – поток числа атомов (ионов) к поверхности поры.

Рассмотрим движение поры, условно предположив, что перенос вещества осуществляется с помощью вакансионного механизма диффузии.

В случае, когда определяющим является механизм объемной диффузии,

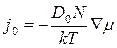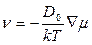, . (3.30)

В конкретном случае движения в поле градиента напряжений, когда ,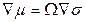

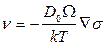. (3.31)

Важной особенностью полученного соотношения является независимость скорости перемещения поры от ее радиуса. Эта зависимость появляется, однако, в случае, когда перенос вещества осуществляется с помощью механизма поверхностной диффузии. Действительно, пусть j_s – плотность потока атомов по поверхности поры. В стационарном режиме перемещения поры (ν = const.) величина j_s не зависит от времени. На различных участках поверхности сферической поры, положение которых определяется полярным углом φ между направлением перемещения поры и нормалью к данному участку ее поверхности, величина j_s(φ) различна и определяется соотношением

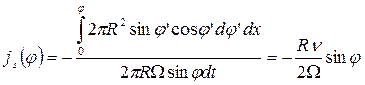. (3.32)

Величина j_s(φ) достигает максимального значения j_m при φ = π/2, и таким образом

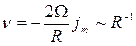. (3.33)

Соотношение (3.33) справедливо безотносительно к тому, каков детальный механизм поверхностной диффузии. Применительно к случаю, когда движение происходит в поле градиента напряжений, скорость определяется соотношением:

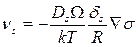(3.34)

Здесь δ_s – толщина приповерхностного слоя, где диффузия осуществляется в меру коэффициента D_s.

С уменьшением размера поры относительная роль механизма поверхностной диффузии будет возрастать и станет определяющей при R < R* = D_sδ_s/D₀. При
D_s/D₀ = 10⁴ – 10⁵ и δ_s^*~ 10^{-9 м}имеем: R* ≈ 10^{-1 м. Числовые оценки величины ν}_s, сделанные с помощью соотношения (3.34), приводят к величине 1 – 10 Å/с.

Экспериментальные исследования движения пор под влиянием градиента напряжений отсутствуют. Имеются, опыты, в которых наблюдалось движение пор под влиянием градиента температуры ( 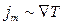и, таким образом, ).

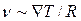Закон v ~ R^-1 наблюдали экспериментально. С помощью электронного микроскопа исследовали перемещение газозаполненных пор в медной фольге в поле градиента температуры. Значительный градиент создавали путем локального разогрева фольги электронным пучком. В этих опытах скорости перемещения пор оказались обратно пропорциональными их радиусам. Поры с радиусами ~3,5×10^{-8 м}перемещались со скоростью ≈10^-7м/с, т.е. за секунду пора перемещалась на расстояние, в несколько раз превосходящее ее линейные размеры (!).

Движение полой поры сопровождается ее залечиванием, и в связи с этим существует некоторая предельная величина смещения

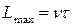, (3.35)

где τ – время полного залечивания поры.

При залечивании с помощью диффузионного растворения τ определяется соотношением (3.20).

В случае, когда перемещение поры с начальным радиусом R₀ осуществляется под влиянием градиента напряжений механизмом объемной диффузии,

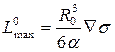, (3.36)

а в случае механизма поверхностной диффузии

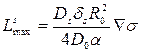. (3.37)

Из (3.36) и (3.37) следует, что при прочих равных условиях

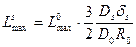. (3.38)

Перемещение поры, осуществляющееся с помощью поверхностной диффузии, в области невысоких температур может оказаться значительным, существенно превосходящим ее размер. Из (3.37) следует, что
L_s^max /R₀ = 10 – 10³ в области невысоких температур, когда D_s/D₀ = 10⁶ – 10⁷.

В реальной порошковой прессовке пора может перемещаться в поле напряжений, создаваемом соседней порой или расположенной поблизости дислокацией.

Выполним оценку кинетики сближения двух полых сферических пор. Величина 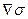, обусловленная близостью поры радиуса R₀, по порядку определяется соотношением

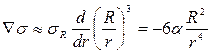, (3.39)

где r – расстояние между порами.

Из соотношений (3.31), (3.34) и (3.39) следуют формулы, определяющие скорость сближения двух пор одинакового радиуса R:

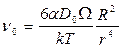, (3.40)

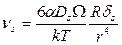. (3.41)

В (3.40) учтена временная зависимость радиуса залечивающейся поры согласно (3.19).

В случае, когда перемещение поры осуществляется вследствие вязкого деформирования среды, скорость сближении двух пор определится формулой

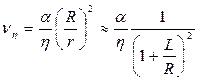, (3.42)

где L = r – R.

Скорость сближения двух пор разного размера (R₁ и R₂) определяется соотношениями, подобными (3.40) и (3.41):

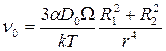, (3.43)

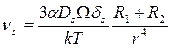. (3.44)

Из приведенных оценок следует, что скорость сближения газозаполненных пор, радиус которых остается неизменным, со временем увеличивается. В случае полых (т.е. залечивающихся) пор скорость их сближения может со временем убывать в связи с тем, что поля напряжений, создаваемые порами, с уменьшением размера пор будут перекрываться в меньшей степени.

Ряд исследователей наблюдали перемещение поры в поле градиента напряжений, создаваемых соседней порой. Изучали сближение пор в монокристаллах NaCl, отжигавшихся в автоклаве под давлением инертного газа 2 – 3 МПа.Давление всестороннего сжатия способствовало ускорению процесса, не изменяя его закономерностей. Для опытов выбирали образцы, имевшие приблизительно изомерные поры с размером 10^-3 – 10^{-4 м. Результаты экспериментов представлены на рис. 3.12 в безразмерных координатах} l/l₀ и d/d₀. В этих координатах удобно представить результат графического интегрирования уравнения (3.42), с которым следует сравнивать экспериментально наблюдаемую кинетику, так как в принятых условиях опыта залечивание пор и сближение центров происходило вследствие вязко-пластического течения вещества. Ход кривой в избранных координатах не зависит от кинетики процесса, а определяется начальным размером пор и их взаимным расположением. Как это следует из рис. 3.12, где приведены расчетные и экспериментально найденные зависимости, соотношение (3.42) достаточно хорошо описывает реально наблюдаемую кинетику сближения центров пор.

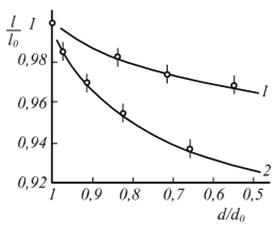
Рис. 3.12. Данные о взаимном сближении двух пор в монокристалле NaCl под давлением.
1, 2 относятся к двум различным парам пор.

Перемещение поры может произойти в поле напряжений, создаваемых дислокацией, находящейся па расстоянии r от центра поры. В этом случае 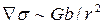(G – модуль сдвига, b – вектор Бюргерса). Имея в виду мелкие поры, когда скорость перемещения определяется механизмом поверхностной диффузии, можно, воспользовавшись (3.34), оценить скорость движения поры в поле, создаваемом дислокацией:

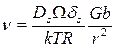. (3.45)

Из (3.45) следует оценка: при D_sδ_s = 10^-18 – 10^-19 м³/с, R = 10^-6 – 10^{-7 м,}
r = 10^{-6 м,} b = 5×10^{-10 м оказывается, что} ν =10^-8 – 10^-9 м/с.

Скорость движения поры может существенно увеличиться, если напряжения создаются не одиночной, а группой дислокаций.

Как уже упоминалось, пора может двигаться, притягиваясь к границе, закрепляясь на ней так, чтобы максимальный участок поверхности границы «исчез» в поре.

Перемещение поры как целого может осуществляться в пористой среде в процессе собирательной рекристаллизации. В этом случае силы, вынуждающие рекристаллизационное смещение границ, концы которых закреплены на поре, искажают ее форму так, что вдоль поверхности поры возникает градиент химического потенциала, который обусловливает поток вещества от «передней» к «задней» стенке поры, т.е. ее смещение в направлении движения межзеренных границ (рис. 3.13). На начальной стадии собирательной рекристаллизации этот механизм движения пор может оказаться действенным и существенно влияющим на кинетику собирательной рекристаллизации и коалесценции пор.

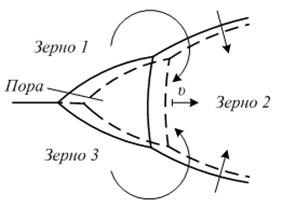
Рис. 3.13. Схема перемещения поры, увлекаемой движущимися границами.
ν – направление движения поры; прямые стрелки – направления движения границ; изогнутые стрелки – направление потока вакансий

В ионном кристалле, где имеются вакансии, несущие эффективные заряды различных знаков, пора может перемещаться в электрическом поле. Если в кристалле создано однородное на бесконечности электрическое поле напряженностью Е, то обусловленное им перемещение поры не может быть вызвано только поверхностной диффузией (в отсутствие объемной). Это обстоятельство – следствие того, что пара ионов двух типов в решетке не обладает суммарным зарядом и поэтому в линейном по электрическому полю приближении их химический потенциал не зависит от электрического поля. Перемещение поры в ионном кристалле под влиянием электрического поля может происходить лишь при условии определенного согласования потоков объемной и поверхностной диффузии. Расчет скорости перемещения поры в ионном кристалле типа NaCl приводит к соотношению

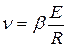; (3.46)

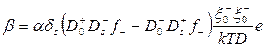; (3.47)

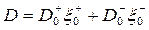, (3.48)

где ξ₀⁺, ξ₀^- и D₀⁺, D₀^- – равновесные концентрации и коэффициенты диффузии вакансий в анионной и катионной подрешетках;

D_s⁺, D_s^- – коэффициенты поверхностной диффузии анионных и катионных вакансий;

δ_s – толщина «приповерхностного» слоя;

e – заряд электрона;

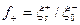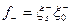, – безразмерные отношения концентрации анионных и катионных вакансий на поверхности и в объеме кристалла.

Рис. 3.14. Последовательность фотографий газозаполненных полостей в NaCl, движущихся под влиянием электрического поля

Экспериментально перемещение пор в монокристалле NaCl под влиянием электрического поля наблюдалось в опытах, проводившихся при
Т = 700 °С и Е = 7 кВ/м(ток через кристалл 0,5 – 0,7 мкА). При этом происходилизначительные взаимные перемещения пор в ансамбле, состоящем из множества пор различных размеров. Типичная серия фотографий одного и того же пористого участка кристалла изображена на рис. 3.14.

Законы v ~ R^-1 и v ~ E в описываемых опытах выполнялись. Скорость перемещения пор при R ≈ 10^{-5 м}и Т = 700 °С оказалась порядка 10^-10 м/с.