Самоорганизующиеся нейронные сети Кохонена

Одной из главных задач, решаемых системой интеллектуальной поддержки, является задача распознавания ситуаций (образов). Эти ситуации не всегда могут быть априори классифицированы и предоставлены системе в виде набора шаблонов. На этот случай в системе должны присутствовать механизмы разбиения воспринимаемых ситуаций на классы (кластеризации) и последующей классификации вновь поступающих образов. Основой для построения таких механизмов могут служить самоорганизующиеся нейронные сети.

Классическим примером самоорганизующейся нейронной сети является сеть Кохонена (самоорганизующаяся карта признаков) [11, 19].

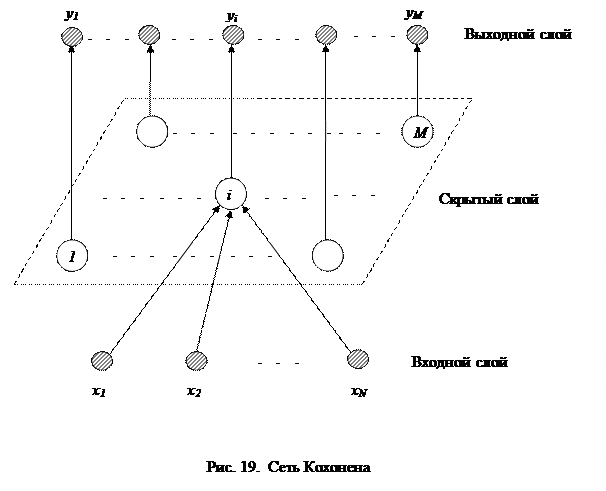
Нейронная сеть Кохонена относится к классу сетей прямого распространения. Она имеет единственный скрытый слой нейронов, представленный в виде одномерной или двумерной решетки (в принципе размерность решетки может быть и выше, случай двумерной решетки показан на рис. 19). Каждому скрытому нейрону соответствует свой выход сети. Нейроны входного слоя, количество которых равно размерности воспринимаемого образа, осуществляют функции приема и ретрансляции входных сигналов на все нейроны скрытого слоя (на рис. 19 это показано только для нейрона 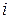). Число нейронов в скрытом слое (и, соответственно, число выходов сети) определяет количество кластеров, на распознавание которых ориентируется нейронная сеть.

Алгоритм, обеспечивающий процесс самоорганизации нейронной сети Кохонена, подбирая синаптические веса связей между нейронами входного и скрытого слоев 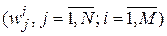, преследует цель отобразить множество N-мерных входных векторов в двумерную карту распределения нейронных активностей. Каждый нейрон такой карты соответствует определенному кластеру, объединяющему в себе сходные по критерию близости векторы. 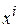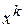В качестве критерия близости векторов и можно использовать евклидово расстояние между ними 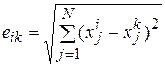или их скалярное произведение 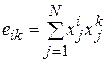(в смысле его максимума).

В основу алгоритма положены три механизма [19]:

· механизм конкуренции;

· механизм кооперации;

· механизм адаптации.

Механизм конкуренции реализует конкурсный (конкурентный) метод, суть которого состоит в следующем.

Входной вектор 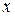и векторы синаптических весов входных связей всех нейронов скрытого слоя ( 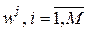) предполагаются нормализованными. Для каждого скрытого нейрона оценивается величина его активности 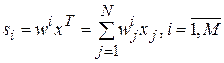. Между нейронами осуществляется конкурс на максимальное значение этой величины. Нейрон 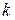, имеющий наибольшее значение нейронной активности 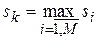, объявляется победителем и наиболее подходящим для данного вектора .

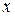Механизм кооперации реализует принцип, согласно которому наиболее возбужденный нейрон усиливает (через синаптические веса) не только себя, но и пространственно близкие к нему нейроны. В связи с этим вводятся понятия топологической окрестности победившего нейрона и функции окрестности 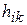, определяющей меру соседства нейрона 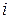с нейроном-победителем 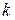. В качестве последней часто используется функция Гаусса

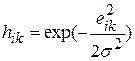, (7.12)

где 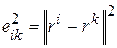, 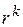и 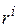— дискретные векторы, определяющие, соответственно, позиции нейрона-победителя 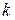и его нейрона-соседа 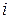в решетке;

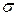— эффективная ширина топологической окрестности, определяющая минимальный уровень функции окрестности, до которого нейроны из топологической окрестности участвуют в процессе обучения вместе с нейроном-победителем.

В процессе обучения эффективная ширина топологической окрестности постепенно уменьшается, например по закону

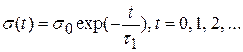, (7.13)

где 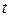— дискретное время;

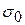— начальное значение величины ;

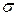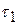— некоторая временная константа (настроечный параметр алгоритма).

Таким образом, функция окрестности приобретает зависимость от времени в виде

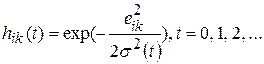, (7.14)

где 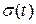определяется по формуле (7.13).

Механизм адаптации реализует определенную стратегию изменения (коррекции) весов синаптических связей. В ее основу может быть положено правило Хебба с некоторой дополнительной составляющей, учитывающей эффект забывания.

Правило Хебба говорит о том, что если предсинаптический и постсинаптический нейроны активизируются одновременно, то сила этой связи возрастает. В противном случае синапс ослабляется.

Эффект забывания учитывается слагаемым (входящим в общую формулу с отрицательным знаком) в ви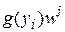де , где 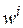— вектор синаптических весов нейрона 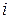; 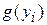— положительная скалярная функция, определенная на дискретном наборе выходных сигналов нейронов (функция забывания) и принимающая нулевое значение для .

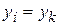С учетом вышесказанного изменение (коррекция) вектора синаптических весов нейрона 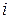представляется следующей формулой:

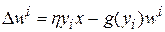, (7.15)

где 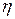— параметр скорости обучения.

Если в качестве функции забывания использовать линейную функцию 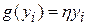и оценивать выходы нейронов функцией окрестности, т.е. принять 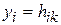, то формула адаптации векторов синаптических весов (7.15), с учетом необходимости их нормирования, примет следующий вид:

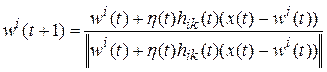, (7.16)

где 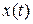— вектор, поданный на вход сети в момент времени ;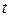

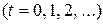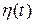— меняющийся во времени (постепенно уменьшаемый) параметр скорости обучения.

В основу изменения параметра скорости обучения может быть положена функция

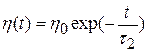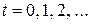, , (7.17)

где 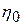— исходное значение параметра (в момент );

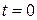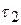— некоторая временная константа (настроечный параметр алгоритма).

Формула (7.16) применяется ко всем нейронам, лежащим в топологической окрестности нейрона-победителя 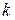и кооперирующимся с ним в обучении. Из формулы видно, что векторы синаптических весов кооперирующихся нейронов 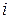смещаются в сторону входного вектора со скоростью, пропорциональной соответствующему им значению функции окрестности (наиболее интенсивно это происходит у нейрона-победителя 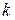, имеющего максимальное значение ).

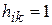Помимо рассмотренных архитектур ИНС, существует множество других, с которыми можно ознакомиться, обратившись к источникам [11, 12, 19].

ВОПРОСЫ И ЗАДАНИЯ ДЛЯ САМОКОНТРОЛЯ

1. Как Вы понимаете аналитический и синтетический способы обработки информации?

2. Какова структура естественного нейрона?

3. Как классифицируются естественные нейроны с точки зрения выполняемых ими функций?

4. Как формируются и передаются нервные импульсы?

5. Какова предельная частота активизации естественного нейрона?

6. Опишите механизм взаимодействия между естественными нейронами.

7. Определите понятие искусственной нейронной сети.

8. Как Вы понимаете словосочетание существенно параллельно распределенный процессор?

9. Что представляет собой классическая модель формального нейрона?

10. Какие виды активационных функций нейронов Вы знаете?

11. Проведите классификацию ИНС по характеру входных сигналов, базовым свойствам структуры и типу обучения.

12. Чем принципиально отличается обучение ИНС с супервизором от обучения через самоорганизацию?

13. Чем отличается многослойный персептрон стандартной (регулярной) топологии от его модифицированных версий?

14. Что означает свойство ИНС обобщать?

15. Попробуйте обучить однослойный персептрон Розенблатта выполнению двуместной логической операции сложения по модулю 2 ( ).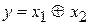

16. Что, на Ваш взгляд, является наиболее ценным в классическом алгоритме обратного распространения ошибки: заложенная в нем стратегия поиска (оптимизации) или возможность вычисления точных (аналитических) производных от функции ошибки по варьируемым параметрам сети?

17. Опишите алгоритм синтеза RBF-сети.

18. Как обучается и функционирует нейронная сеть Хопфилда?

19. Сколько образов может запомнить сеть Хопфилда?

20. Как обучается и функционирует нейронная сеть Хемминга?

21. Сколько образов может запомнить сеть Хемминга?

22. Назовите основные механизмы, положенные в основу самоорганизации нейронной сети Кохонена. В чем суть каждого из них?

8. НЕКОТОРЫЕ ИЗ ПРИЛОЖЕНИЙ
ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ