Классификация искусственных нейронных сетей

Конкретные типы архитектур ИНС различаются [12, 19]:

· характером входных сигналов;

· структурой сети;

· типом обучения.

По характеру входных сигналов сети могут быть бинарными или аналоговыми.

Бинарные сети принимают на свои входы сигналы, имеющие значения 0 или 1. Иногда рассматривают (как вариант бинарной сети) биполярные сети, оперирующие с сигналами, принимающими значения 1 или -1.

Аналоговые сети работают с сигналами из непрерывного спектра значений. Например, с нормированными сигналами, принимающими значения на отрезке [-1, 1].

По характеру структуры нейронные сети можно разбить на два больших класса, принципиально отличающихся друг от друга признаком отсутствия или наличия в сети межнейронных обратных связей:

· нейронные сети прямого распространения;

· рекуррентные нейронные сети.

Нейронные сети прямого распространения обычно представляются в виде многослойных (в частном случае однослойных) структур, обладающих свойством прямонаправленности: каждый нейрон предыдущего слоя (начиная с входного слоя) может воздействовать только на нейроны последующих слоев и ни на какие другие.

Рекуррентные нейронные сети отличаются от сетей прямого распространения наличием в них обратных связей.

По типу обучения различают нейронные сети:

· обучаемые с супервизором (с учителем);

· обучаемые через самоорганизацию.

Обучение с учителем предполагает наличие множества обучающих шаблонов. Каждый шаблон ставит в соответствие конкретному входному воздействию на сеть (из множества возможных воздействий) требуемый от нее (желаемый) отклик. В процессе обучения настроечные параметры сети (синаптические веса межнейронных связей, пороги и, возможно, параметры активационных функций нейронов) подбираются таким образом, чтобы реальные отклики сети на входные воздействия, указанные в шаблонах, совпадали (с определенной степенью точности) с желаемыми. При достаточной мощности нейронной сети (в смысле количества слоев, числа нейронов в них) и множества обучающих шаблонов сеть приобретает способность правильно реагировать не только на входные воздействия из обучающей выборки, но и на другие допустимые незнакомые ей воздействия. В этом состоит свойство нейронной сети обобщать.

Обучение нейронной сети через самоорганизацию осуществляется без контроля со стороны учителя (множества обучающих шаблонов). Обучение осуществляется только по входным образам с использованием независимой от задачи меры качества ее представления, которому должна научиться нейронная сеть.

Рассмотренная классификация проведена только по основным признакам, характеризующим конкретные архитектуры нейронных сетей с точки зрения принципов их обучения и функционирования.

Персептроны

Многослойный персептрон представляет собой сеть прямого распространения с одним входным (сенсорным)слоем, одним выходным (моторным) слоем и одним или несколькими внутренними (скрытыми, связующими) слоями нейронов. Характерной его чертой является прямонаправленность: информация, преобразуясь, передается от входного слоя через 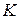скрытых слоев к выходному слою.

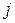
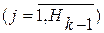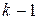
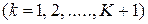В стандартной (регулярной) топологии персептрона каждый нейрон слоя непосредственно воздействует с синаптическими весами 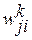на все нейроны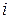 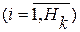следующего слоя 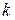и ни на какие другие ( 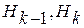– соответственно, число нейронов в слое 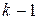и в слое 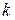; 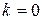и 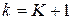обозначают, соответственно, входной и выходной слои). Схема многослойного персептрона стандартной топологии представлена на рис. 14.

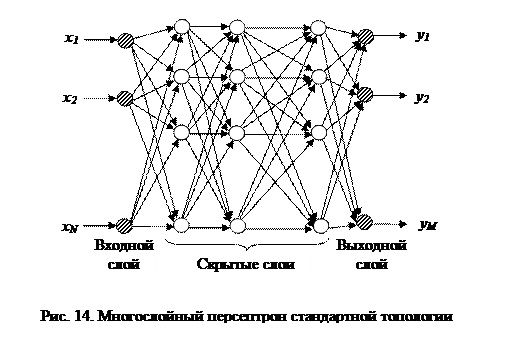
Модифицированные версии многослойного персептрона могут иметь нерегулярные связи между слоями (какие-то связи могут отсутствовать) и прямые (непосредственные) связи между нейронами несмежных слоев.

Входной слой персептрона выполняет функции приема и ретрансляции входных сигналов 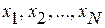на нейроны первого скрытого слоя. Основное нелинейное преобразование сигналов происходит в скрытых слоях. Нейроны выходного слоя осуществляют суперпозицию взвешенных сигналов последнего скрытого слоя (имеют линейную активационную функцию) или выполняют нелинейное преобразование, как и нейроны скрытых слоев.

Обучение персептрона – это итеративный целенаправленный процесс изменения значений весов синаптических связей (и, возможно, порогов активационных функций нейронов), реализуемый «внешней» процедурой (алгоритмом обучения) с использованием тренировочных шаблонов (обучение с супервизором) до тех пор, пока сеть не приобретет желаемые свойства.

Тренировочный шаблон представляет собой пару векторов 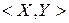, один из которых 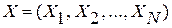– вектор известных входных сигналов, другой 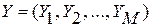– вектор желаемых выходных сигналов. В процессе обучения векторы 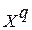из тренировочного набора 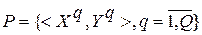последовательно подаются на вход ИНС и для каждого из них оценивается ошибка между фактическим 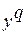и желаемым 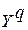откликом (выходом) сети 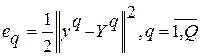. Затем определяется общая ошибка 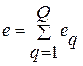, на основании которой (а возможно, и с использованием данных о предыдущих итерациях) алгоритм обучения осуществляет модификацию значений настроечных параметров сети, направленную на уменьшение ошибки. Как вариант, модификация значений варьируемых параметров сети может осуществляться после оценки действия каждого очередного шаблона, т.е. по «локальной» ошибке 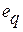. Процесс обучения повторяется до тех пор, пока сеть не приобретет способность выполнять желаемый тип преобразования, заданный тренировочным набором шаблонов .

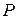В результате обучения сеть достигает способности правильно реагировать не только на шаблоны множества 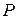, но и на другие допустимые возмущения, с которыми она никогда ранее не имела дела. В этом состоит уже упоминавшееся свойство ИНС обобщать. Ошибка в обобщении, которая может иметь место, определяется двумя причинами:

· ограниченностью размеров сети, ведущей к недостаточному качеству аппроксимации;

· ограниченностью объема обучающей выборки.

Схема, иллюстрирующая процесс обучения персептрона, представлена на рис. 15.

Рассмотрение проблемы обучения начнем с простейшего однослойного персептрона Розенблатта (рис. 16).

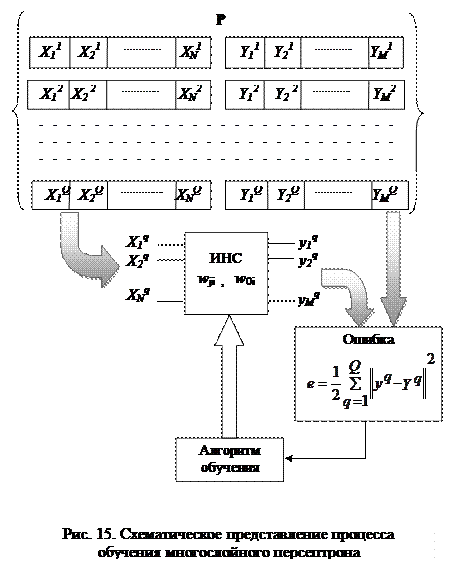
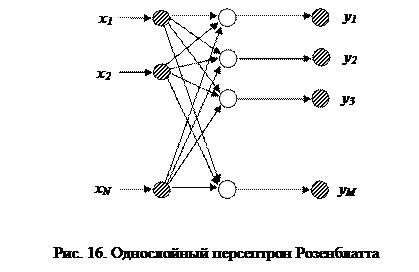
Это нейронная сеть, имеющая 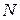входов и один слой из 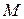связующих нейронов, передающих сигналы каждый на свой выход. Входной слой выполняет функции приема и ретрансляции входных сигналов 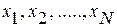на нейроны скрытого слоя, 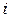-й связующий нейрон которого 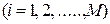осуществляет нелинейное преобразование

,

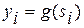где 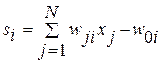— сдвинутая на величину порога 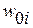сумма взвешенных входных сигналов;

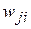— синаптический вес связи 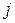-го нейрона входного слоя с 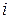-м нейроном скрытого слоя;

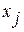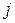— -й входной сигнал сети (бинарный или непрерывный);

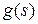– ступенчатая активационная функция нейрона;

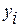– переменная, характеризующая выход i-го интернейрона и принимающая значения 0 или 1.

Согласно данному закону функционирования, однослойный персептрон Розенблатта разделяет 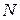-мерное пространство входных сигналов на классы гиперплоскостями:

, .

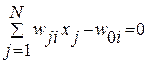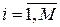Таких классов может быть не более .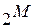

Для однослойного персептрона Розенблатт использовал следующее правило обучения: веса связей увеличиваются, если выходной сигнал, сформированный принимающим нейроном, слишком слаб, и уменьшаются, если он слишком высокий. Согласно этому правилу, веса связей 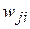менялисьпосле каждого вычисления выходов нейронной сети 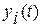для поданного на вход очередного вектора из набора шаблонов по следующей формуле:

,

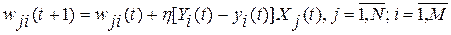где 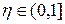— настроечный параметр процедуры обучения.

Для обучения многослойных персептронов Вербосом в 1974 году был предложен алгоритм обратного распространения ошибки (АОР, или BPE – Back-Propagation Error).

В основу алгоритма BPE положен метод градиентного спуска, согласно которому на каждой итерации поиска значений синаптических весов и порогов активационных функций нейронов, направленной на уменьшение ошибки 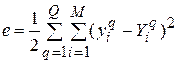, их приращения определяются по формулам:

, , ; ; ,

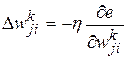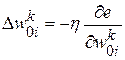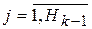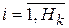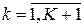где 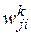— синаптический вес связи j-го нейрона (k–1)-го слоя с i-м нейроном k-го слоя;

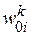— порог активационной функции i-го нейрона k-го слоя;

H_k – число нейронов в k-м слое;

hÎ(0,1]— настроечный параметр обучения.

Согласно правилу дифференцирования сложной функции, производная от функции ошибки по 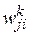определяется как

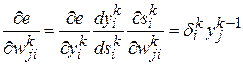, (7.1)

где 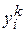— сигнал на выходе i-го нейрона k-го слоя;

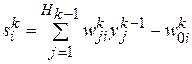— сдвинутая на величину порога сумма взвешенных входных сигналов i-го нейрона k-го слоя; .

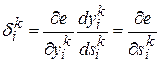Надо заметить, что выражение (7.1) и все последующие выкладки приведены для случая оценки локальной ошибки 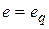(для одного шаблона), поэтому индекс шаблона везде опущен.

Представление производной 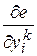через выходы нейронов (k+1)-го слоя

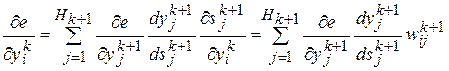(7.2)

позволяет получить рекурсивную формулу

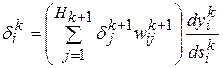(7.3)

для пересчета величин 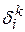со слоя k+1 на слой k (то, что называют обратным распространением ошибки).

Очевидно, для слоя K+1(выходного слоя), с которого начинается обратное распространение ошибки,

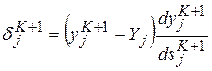. (7.4)

Таким образом, итерационная формула для коррекции значений синаптических весов принимает следующий вид:

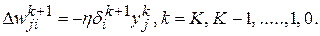(7.5)

Аналогично получается итерационная формула коррекции значений порогов активационных функций нейронов:

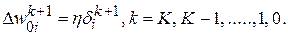(7.6)

Выбор той или иной активационной функции определяется многими факторами, среди которых в первую очередь следует выделить существование производной на всей оси абсцисс и удобство организации вычислений. С учетом этих факторов в алгоритме BPE чаще используют сигмоидальную активационную функцию. Для нее, согласно (7.4),

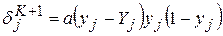. (7.7)

В формуле (7.7) 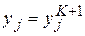— сигнал на выходе j-го нейрона выходного слоя персептрона.

В итоге общее описание алгоритма BPE можно представить следующим образом:

П1. Инициализация синаптических весов 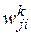и порогов активационных функций 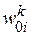во всех слоях персептрона ( 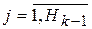, , 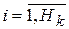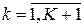) как маленьких величин, например отрезка [-1,1].

П2. Выбор очередного шаблона 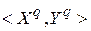из множества P случайным образом или согласно определенному правилу.

П3. Прямой ход: вычисление фактических выходов нейронов персептрона по формуле:

, , , ;

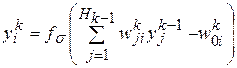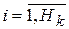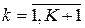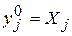вычисление ошибки и проверка критерия выхода из алгоритма.

П4. Обратный ход: коррекция значений синаптических весов и порогов активационных функций с использованием выражений (7.3)–(7.7).

П5. Переход к П2.

7.5. RBF-сеть

RBF-сеть (Radial Basis Function-network) представляет собой однослойную (по числу скрытых слоев) ИНС (рис. 17) прямого распространения, способную аппроксимировать произвольный набор непрерывных функций в базисе радиально-симметричных активационных функций нейронов с любой степенью точности, обучаясь с супервизором по простому алгоритму, не требующему рекурсии.

Аппроксимируемые функции задаются набором шаблонов

,

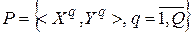где 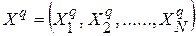— вектор переменных (аргументов) аппроксимируемых функций, определяющий N-мерное пространство входных сигналов RBF-сети;

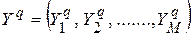— вектор соответствующих значений аппроксимируемых функций, число которых M определяет количество выходов RBF-сети.

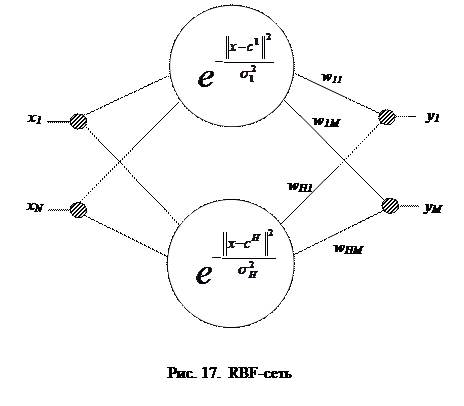
RBF-сеть имеет единственный скрытый слой из H нейронов. Только эти нейроны, обладая радиально-симметричной активационной функцией, осуществляют нелинейное преобразование. Синаптические веса всех связей между нейронами входного и скрытого слоев берутся равными единице.

В активационной функции i-го нейрона скрытого слоя, описываемой выражением

,

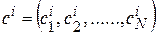— центр активационной функции i-го нейрона скрытого слоя;

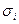— ширина окна активационной функции i-го нейрона.

Матричное выражение для вычисления синаптических весов связей между нейронами скрытого и выходного слоев ( 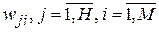) получается следующим образом.

Сигнал выхода i-го нейрона выходного слоя, получаемый под воздействием вектора аргументов q-го шаблона ( 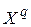), приравнивается i-му элементу 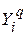выходного вектора этого шаблона:

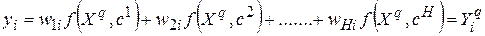. (7.8)

Если положить 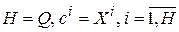, то уравнение (7.8) можно представить в следующем виде:

,

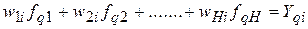где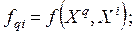

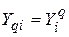— желаемый отклик i-го выходного нейрона на q-й шаблон.

Записав аналогичные уравнения для всех выходов сети и всех шаблонов, получим следующее матричное уравнение:

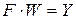, (7.9)

где ; ;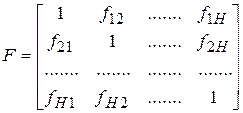

.

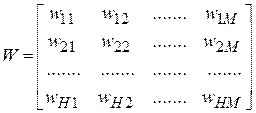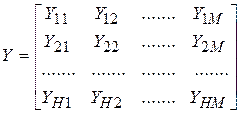Из (7.9) легко находится матрица синаптических весов

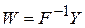. (7.10)

С учетом вышеизложенного синтез RBF-сети осуществляется по следующему алгоритму:

П1. Определяется размер H скрытого слоя RBF-сети, равный количеству тренировочных шаблонов Q (H=Q).

П2. В качестве центров активационных функций нейронов скрытого слоя берутся точки пространства входных сигналов, заданные в наборе тренировочных шаблонов Р, т.е.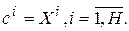

П3. Задается ширина окон активационных функций нейронов скрытого слоя 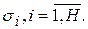Окна должны покрывать пространство входных сигналов сети, не накладываясь друг на друга.

П4. Формируются матрицы F и Y.

П5. Вычисляется матрица 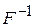, и по формуле (7.10) определяются значения синаптических весов 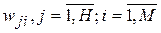, обеспечивающие совпадение точек интерполяционной поверхности с тренировочными шаблонами в пространстве выходных сигналов сети.

Следует заметить, что наиболее ответственными этапами описанного алгоритма являются выбор размера скрытого слоя и задание ширины окон активационных функций его нейронов. Ибо от этого зависит ошибка аппроксимации в точках входного пространства, не фигурирующих в наборе тренировочных шаблонов.

Сеть Хопфилда

Сеть Хопфилда относится к классу рекуррентных ИНС. Она состоит из N нейронов, каждый из которых имеет связи воздействия на все остальные нейроны (полный направленный граф без петель) с весами 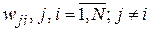. Выходы нейронов фиксируют начальное состояние сети, обусловленное предъявленным стимулом (возмущением), и все последующие ее состояния вплоть до устойчивого.

Состояние бинарной сети Хопфилда описывается N-мерным вектором 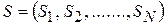, компонента 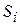которого характеризует состояние i-го нейрона: 0 или 1 (имеется в виду использование в качестве активационной функции нейрона единичной ступеньки). Таким образом, состоянию сети соответствует одна из вершин единичного гиперкуба в N-мерном пространстве.

Каждое устойчивое состояние такой системы можно рассматривать как «запись образа» в ее памяти. При подаче на ее входы возмущения, обусловленного предъявленным для распознавания образом, сеть должна из приобретенного начального состояния в соответствии с динамикой ее функционирования прийти в устойчивое состояние, определяющее идеальный записанный образ.

Возможна асинхронная или синхронная динамика поведения сети.

В случае асинхронной динамики состояние сети меняется с определенной частотой так, что в каждый следующий момент времени случайно выбранный нейрон i принимает состояние

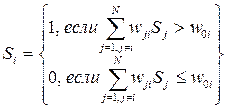, (7.11)

где 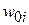— порог i-го нейрона, который часто принимается равным 0 для всех .

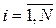В отличие от асинхронной динамики, синхронная динамика предполагает изменение в каждый момент времени по правилу (7.11) состояния всех нейронов сети.

Хранение образов 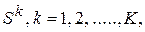в памяти сети Хопфилда обеспечивается матрицей синаптических весов, известной под названием матрица Хебба. Ее элементы определяются по формулам:

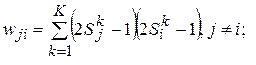
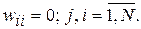
Надежное распознавание образов сетью Хопфилда обеспечивается при выполнении соотношения .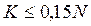

Сеть Хемминга

Это нейронная сеть, состоящая из двух однослойных подсетей A и B, содержащих по M нейронов (рис. 18). Подсеть A формирует по входному N-мерному бинарному вектору начальные состояния ( 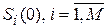) для нейронов подсети В согласно выражению:

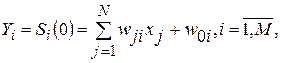
где 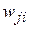— синаптический вес связи 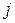-го нейрона входного слоя с 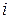-м нейроном подсети А;

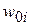— порог линейной активационной функции 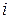-го нейрона подсети А.

При настройке подсети А значения синаптических весов и порогов определяются по формулам:

,

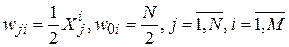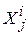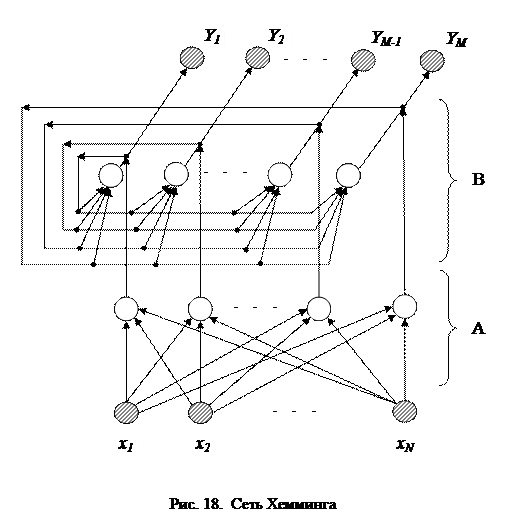
где — 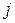-й элемент 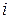-го вектора памяти.

Динамика подсети В итерационна. От начального состояния, установленного подсетью А, она развивается по закону:

,

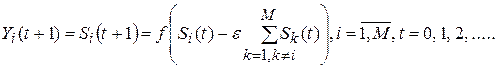где 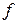– пороговая активационная функция нейронов подсети В, аргумент которой записан с учетом синаптических весов обратных связей, определенных по формуле:

; .

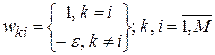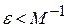Пороги активационных функций для нейронов подсети В устанавливаются равными 0.

Итерационный процесс заканчивается, когда выходы всех нейронов подсети В, за исключением одного, становятся пассивными (побеждает один, соответствующий идентифицированному идеальному образу). Следует заметить, что в случае когда один из векторов памяти является частью (по значащим фрагментам кода) другого вектора, при подаче его на вход сети активными становятся выходные нейроны, соответствующие обоим векторам.

Таким образом, обученная сеть Хемминга, как и сеть Хопфилда, способна выполнять функции ассоциативной памяти, т.е. распознавать (воссоздавать) идеальный образ по предъявленной искаженной информации о нем. Число запоминаемых сетью образов равно