Синтез автономной системы управления спускаемым аппаратом

Обратимся снова к задаче синтеза автономной системы управления конечным состоянием спускаемого аппарата. Целью управления по-прежнему является обеспечение минимального рас­сеивания точек приземления, которое возникает за счет случайных возмущений, действующих в полете (порывы ветра, отклонение плотности атмосферы от стандартной, отклонения геометрических и аэродинамических параметров от расчетных). Однако в отличие от случая управления по полной информации, рассмотренного в гл. 5, теперь предполагается использовать для управления лишь информацию от акселерометров, ориентированных вдоль связанных осей ЛА.

Ограничимся рассмотрением плоского движения центра масс ЛА, полагая, что оно может быть достаточно точно описано линеа­ризованными относительно расчетной траектории спуска уравнениями движения типа (5.83)

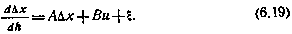
Предполагается, что в состав вектора состояния х включены пара­метры, описывающие как движение центра масс, так и динамику ЛА относительно центра масс в продольной плоскости.

В соответствии с постановкой задачи измерению доступен век­тор перегрузки п с компонентами

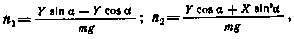
где X — сила лобового сопротивления; Y — подъемная сила; 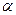— угол атаки, т — масса ЛА.

Линеаризуя выражения для перегрузок относительно расчетной траектории, получаем

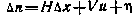
или

где 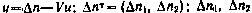— отклонения соответст­вующих перегрузок от их расчетных значений; Н, V—матрица и вектор частных производных по компонентам вектора х и управ­лению и соответственно, вычисленные вдоль расчетной траектории; — белый шум, характеризующий случайные ошибки измерений, причем

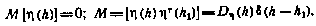
В качестве характеристики рассеивания примем, как и прежде, дисперсию координаты 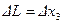в момент h=0. Тогда задача оптимизации математически может быть сформулирована так: тре­буется синтезировать закон управления системой (6.19) на основе наблюдений (6.20) из условия минимизации величины

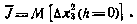
Имеем типичную задачу управления по неполным данным. Для ее решения воспользуемся понятием достаточных координат. В ка­честве вектора достаточных координат может быть принят вектор апостериорного математического ожидания 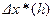, удовлетворяю­щий уравнению

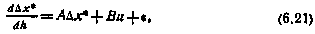
где

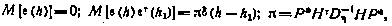
a матрица Р* определяется из уравнения

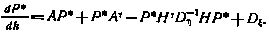
Критерий оптимальности также представим через вектор х*:

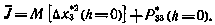
Здесь через 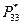обозначен элемент матрицы Р*, стоящий на пересе­чении третьей строки и третьего столбца и представляющий собой апостериорную дисперсию компоненты 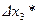. Итак, в терми­нах достаточных координат получена задача управления одномер­ным конечным состоянием линейной системы (6.21). Ее решение было получено в гл. 5. Согласно этому решению искомый закон управления в данном случае имеет вид

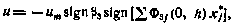
где 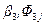определяется так же, как и в гл. 5.

Таким образом, оптимальный стохастический регулятор, обес­печивающий минимальное рассеивание точек приземления ЛА, представляет собой последовательное соединение двух блоков — блока определения достаточных координат (в данном случае фильтра Калмана) и блока управления, который служит для фор­мирования управляющего сигнала на основе достаточных коорди­нат и является в данном случае релейным элементом. Для реали­зации синтезированной системы управления необходимо использо­вать бортовую ЦВМ.