Оптимальное управление сближением летательных аппаратов. линейные непрерывные системы, оптимизируемые по квадратичному критерию

Рассмотрим задачу формирования оптимального алго­ритма (закона) управления при сближении двух летательных ап­паратов, один из которых пассивен и движется по известной (опорной) траектории. В качестве математической модели процесса сближения примем линеаризованные относительно опорной траек­тории уравнения относительного движения второго (активного) летательного аппарата:

где вектор х характеризует отклонение параметров движения двух аппаратов; u — вектор управляющего воздействия активного ап­парата, например, компоненты ускорения, создаваемого двигатель­ной установкой; А и В— матрицы частных производных правых частей нелинейных уравнений движения, получаемые в результате линеаризации нелинейных уравнений движения. В общем случае матрицы А и В зависят от времени. Будем полагать, что возмуще­ние | является белым шумом.

Критерий оптимальности зададим в виде

где — положительно определенные матрицы.

Первое слагаемое (интегральное) в критерии (5.80) характери­зует качество процесса управления (через слагаемое ) и энер­гетические затраты, необходимые для осуществления процесса сближения (через слагаемое ), второе — эффект управления конечным состоянием или, другими словами, точность сближения.

Задача заключается в выборе закона управления u(х,t), обра­щающего критерий (5.80) в минимум. Предполагается, конечно, что в любой момент вектор состояния х может быть измерен. Можно предложить два подхода к решению данной задачи.

Первый заключается в замене непрерывной задачи ее дискрет­ным аналогом, решении полученной дискретной задачи и переходе снова к непрерывному случаю. Дискретными аналогами уравнения движения и критерия оптимальности в данном случае являются

Здесь введены следующие обозначения:

I — единичная матрица; 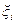— случайный вектор с характеристиками (5.75). Заметим, что из соотношений (5.75) следует, что

Учитывая полученные ранее результаты в отношении линейной дискретной системы с квадратичным критерием, алгоритм оптималь­ного управления для данной задачи можем представить в виде

Причем

Матрица Λ_i, формирующая функцию будущих потерь

определяется с помощью рекуррентного соотношения

при условии Λ_N+1=λ. Наконец, параметр с_i равен

Переходя в этих соотношениях к пределу при 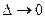, получим ре­шение исходной непрерывной задачи в следующем виде: для функции будущих потерь

для алгоритма оптимального управления

где матрица коэффициентов обратной связи удовлетворяет соотно­шению

а матрица Λ и параметр с — дифференциальным уравнениям

с граничными условиями .

Как и в дискретном случае, алгоритм оптимального управления является линейным. Нетрудно установить, что он полностью совпа­дает с алгоритмом управления соответствующей детерминирован­ной системой (при ). Таким образом, наличие аддитивного возмущения 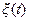в линейной системе не влияет на алгоритм опти­мального управления при использовании квадратичного критерия, а сказывается лишь на величине функции будущих потерь R(x,t) и, следовательно, на общем значении критерия J.

Другими словами, синтез таких систем можно производить, не учитывая аддитивных случайных возмущений. Влияние их следует оценивать лишь при анализе работы замкнутой системы.

Второй подход к решению исходной задачи заключается в не­посредственном применении стохастического уравнения Беллмана (5.76):

Граничное условие при этом принимает вид

Найдем характеристики а, b марковского случайного процесса в данном случае. Раскрывая в (5.77) пределы, получаем

Таким образом, вектор сноса случайного процесса представля­ет собой правую часть уравнения (5.79) при отсутствии возмуще­ния, а матрица интенсивностей совпадает с матрицей интенсивностей белого шума и не зависит ни от х, ни от u.

С учетом найденных значений a(x,u) и b уравнение Беллмана принимает вид

откуда следует, что алгоритм оптимального управления связан с функцией R(x, t) соотношением

С учетом этого соотношения окончательно получаем следующее уравнение для функции :

Покажем, что решение этого уравнения с учетом требуемого граничного условия имеет вид квадратичной формы:

Действительно, подставляя в уравнение, получаем

Последнее уравнение обращается в тождество при любых х, если матрица Λ и скаляр с удовлетворяют системе обыкновенных диф­ференциальных уравнений

Для выполнения граничного условия достаточно потребовать, чтобы

Алгоритм оптимального управления с учетом найденной функции принимает уже известный вид

где матрица коэффициентов обратной связи L равна