Достаточные условия оптимальности в непрерывном случае. стохастическое уравнение беллмана

Обобщим полученные выше результаты на случай управления непрерывными системами. С этой целью дискретизируем непрерыв­ную задачу, применим к полученной дискретной задаче известные результаты и осуществим обратный (предельный) переход к не­прерывной задаче. Начнем с достаточных условий оптимальности.

Пусть динамическая система описывается стохастическим диф­ференциальным уравнением

где х — n-мерный вектор состояния; u — m-мерный вектор управ­ления; 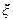— q-мерный вектор случайных возмущений; t — время; f — вектор-функция размерности n.

Рассмотрим поведение системы (5.73) на конечном интервале времени [О, Т], полагая, что управление 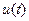принадлежит некото­рому допустимому множеству U(t). Так как практически любое слу­чайное возмущение может рассматриваться как результат прохож­дения белого шума через некоторую динамическую систему, назы­ваемую формирующим фильтром, то, не нарушая общности, можно сказать, что 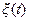является белым шумом с нулевым математиче­ским ожиданием

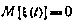
и корреляционной функцией

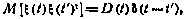
где D(t)—матрица интенсивностей белого шума. Случайный про­цесс x(t), описываемый при этом дифференциальным уравнением (5.73), является марковским.

Полагая, что вектор состояния может быть измерен в любой момент времени, поставим задачу определения такого закона уп­равления u(x,t), который обеспечивает достижение минимума критерия оптимальности

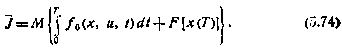
Предположим, что непрерывный процесс 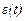может быть представ­лен в виде дискретной последовательности случайных независимых, векторов 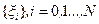, с характеристиками

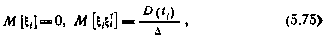
которая при 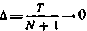в стягивается к процессу 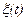. Тогда для всех малых значений Δ вместо уравнения (5.73) и критерия (5.74) можно записать

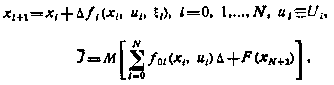
где

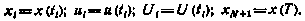
Получили дискретный аналог исходной задачи. Достаточные ус­ловия оптимальности для нее состоят в применении рекуррентного соотношения

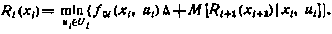
Напомним, что по определению функция 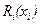равна

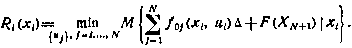
Предположим, что функция 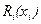имеет частные производные первого и второго порядка для всех i. Разложим функцию 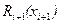в ряд Тейлора в окрестности точки с точностью до членов второ­го порядка малости. Получим

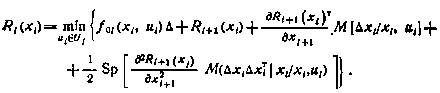
Разделим теперь обе части этого уравнения на Δ и перейдем к пределу при 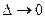. Получим следующее уравнение для R(x,t):

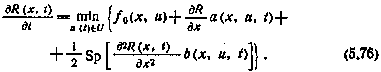
Здесь введены обозначения

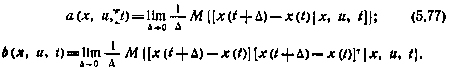
Вектор коэффициентов сноса a(x,и,t) и матрица коэффициентов диффузии b(x,и,t) марковского случайного процесса x(t) харак­теризуют соответственно математическое ожидание и ковариации смещения из точки (x,и) в момент t за время Δ.

Уравнение (5.76) часто называют стохастическим уравнением Беллмана. Решая его, можно найти функцию R(x,t) и параллельно алгоритм оптимального управления системой (5.73). Уравнение (5.7G) является дифференциальным уравнением в частных произ­водных второго порядка.

Граничные условия, которым должно удовлетворять это уравне­ние, получаются из рассмотрения функции R(x,t) в момент t=T. Так как при 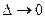функция будущих потерь принимает вид

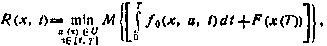
то для момента t=T имеем

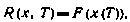
Соотношение (5.78) и следует рассматривать как граничное ус­ловие для уравнения Беллмана (5.76).