Оптимизация процесса перевода стационарного исз в заданное положение с использованием двигательной установки малой тяги

В качестве еще одного примера решения прикладной за­дачи рассмотрим задачу оптимизации процесса перевода стационар­ного ИСЗ (СИСЗ) из одной точки в другую с использованием кор­ректирующей двигательной установки (КДУ) малой тяги, развива­ющей постоянное (в номинале) ускорение вдоль нормали к текуще­му радиус-вектору. Как и в разд. 5.4, перевод СИСЗ должен быть осуществлен с требуемой точностью при минимальных энергетиче­ских затратах. Ввиду малости управляющего ускорения будем те­перь учитывать влияние длительности коррекции, считая его суще­ственным, на параметры текущей орбиты. Это требует использова­ния более сложной модели процесса перевода. Такая модель может быть получена, в частности, если рассмотреть уравнения движения СИСЗ, линеаризованные относительно стационарной орбиты [19]:

Здесь — отклонения радиуса орбиты и долготы от соответ­ствующих значений на стационарной орбите: ; r₀ — радиус стационарной орбиты; — угловая скорость собствен­ного вращения Земли; f — управляющее ускорение, развиваемое КДУ; t — время.

Предположим, что каждое очередное включение КДУ возможно лишь спустя некоторое время после предыдущего выключения. Обозначим через 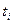момент окончания (t—1)-й коррекции; — дли­тельность i-го пассивного участка; —длительность проведения i-й коррекции. Тогда будем иметь , , 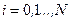N — число коррекций, и — начальный и конечный моменты времени соответственно. Считается, что , , 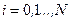— заданные величины.

Полагая, что во время каждой коррекции управляющее ускоре­ние / постоянно и равно ft, согласно [34] решение системы (5.63) можно представить в виде

где

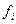la, — номинальное управляющее ускорение, численно равное номи­нальному , но имеющее знак , т. е. — центриро­ванная случайная величина с дисперсией , учитывающая разбро­сы ускорения 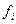относительно номинального значения.

Перейдем в уравнениях системы (5.64) от переменных к новым переменным . Нетрудно установить на основе (5.65), что такой переход является взаимооднозначным. Физический смысл новых переменных сводится к следующему: компонента Хц представляет собой текущее отклонение СИСЗ по долготе от требуемой точки «висения»; компонента , численно равная смещению спутника по долготе в пассивном полете за одни сутки ( при ), характеризует текущую ско­рость дрейфа; наконец, компоненты Хы, Хщ связаны с эксцентриси­тетом текущей орбиты соотношением

Действительно, в i-й момент времени эксцентриситет можно вычис­лить по формуле

где — наибольшее и наименьшее отклонение радиуса орби­ты от стационарного при . Так как согласно (5.64)

то сразу получаем (5.66).

В новых переменных уравнение движения СИСЗ можно пред­ставить в следующем виде:

где

Величина 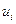, введенная во втором уравнении системы (5.67), имеет важное значение для рассматриваемой задачи. Она характе­ризует расчетное приращение скорости дрейфа в i-й коррекции и однозначно связана с длительностью этой коррекции и направлени­ем приложения управляющего ускорения:

Будем считать 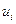в качестве одного из основных параметров управ­ления в i-й момент времени.

На основе соотношения (5.66) и уравнений (5.67) нетрудно полу­чить уравнение для эволюции эксцентриситета в процессе t'-ro кор­ректирования:

где

Из уравнения (5.69) видно, что эксцентриситет после совершения каждой коррекции в общем случае определяется величиной и на­правлением управляющего ускорения, длительностью коррекции и временем ее проведения (месторасположения), определяемым па­раметром , или, что то же самое, длительностью пассивного участ­ка .Исключение составляет лишь случай, когда . Нетрудно убедиться, что эксцентриситет после коррекции в этом случае, рав­ный

зависит лишь от величины управляющего ускорения и длительности коррекции , время проведения коррекции может быть любым.

В связи с тем, что эксцентриситет в конечном счете — явление не­желательное, время проведения каждой коррекции выберем так, чтобы эксцентриситет после коррекции был минимально возмож­ным. Согласно (5.69) минимальное значение достигается при значениях

Здесь — любое целое число, равное

где

Угол может быть определен как

В свою очередь, согласно (5.67) устанавливаем

Откуда при

Поэтому, считая для всех i, получаем окончательно следующее выражение для оптимального значения параметра :

Где

Длительность пассивного участка связана согласно (5.65) с величиной соотношением

Так как однозначно связано с и, следовательно, с целочис­ленным параметром , то последний может быть принят в качест­ве второго управляющего параметра в момент 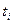(наряду с ),

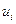С учетом выражений (5.68), (5.70) первое уравнение системы (5.67) можно представить в виде

или

где хн — новая обобщенная переменная, равная

Так как в конце процесса перевода (при ) переменные становятся достаточно малыми, величина по-прежне­му характеризует конечную ошибку по долготе.

Учитывая это, в качестве математической модели при оптимиза­ции процесса перевода СИСЗ примем следующие уравнения:

или более компактно

где

Теперь сформулируем математически задачу оптимизации. Тре­буется найти такие последовательности и , которые обеспечили бы перевод системы (5.71) из начального состояния в конечное с требуемой точностью (если это, конечно, возможно) при минималь­ных энергетических затратах. Энергетические затраты будем оцени­вать величиной

В качестве характеристики конечной точности примем матема­тическое ожидание величины

Итак, требуется минимизировать величину 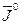при условии

где 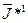— некоторая заданная величина, характеризующая допус­тимые конечные ошибки.

Для решения сформулированной задачи обратимся к комбини­рованному методу оптимизации.

Составим обобщенный критерий оптимальности

где 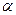— множитель Лагранжа, подлежащий в последующем опре­делению. Как и в разд. 5.4, множитель а следует искать как неот­рицательный корень уравнения

В искомом управлении выделим две составляющие — програм­мную и синтезируемую. К программной отнесем целочисленную по­следовательность , к синтезируемой — последо­вательность . В отношении этих составляющих применим поэтапную оптимизацию.

На первом этапе найдем синтезируемую составляющую. С этой целью обратимся к основному рекуррентному соотношению метода динамического программирования. В данном случае оно принимает вид

причем для момента i = N+ 1

Трудность данной задачи связана с нелинейностью системы (5.71): матрица Ai (точнее, один ее элемент) зависит от управле­ния и переменной а, в уравнение для входит модуль и триго­нометрическая функция с аргументом, содержащим . Для полу­чения приближенного решения аппроксимируем функцию синуса, считая , и линеаризуем уравнение для , «замора­живая» пока матрицу , т. е. считая ее не зависящей от параметров и», а и обозначая через .

Рассмотрим последнюю коррекцию i = N. С учетом сделанных замечаний будем иметь

Где

Отсюда находим, что оптимальное управляющее воздействие на последней коррекции равно

где

а функция будущих потерь при этом

где

Для получения решения при других i<N воспользуемся мето­дом параметров. Аппроксимируем функцию R_N квадратичной. Наи­более просто в данном случае это делается путем пренебрежения вторым слагаемым в выражении для R_N:

Так как вид функции по сравнению с R_N+1 сохранился прежним, то, повторяя изложенные рассуждения, получим аналогичную струк­туру управления и для предыдущей (N—1)-й коррекции. Поэтому аппроксимируя функцию будущих потерь для любого i квадратич­ной функцией вида

получим следующий алгоритм субоптимального управления:

где параметры определяются формулами

Здесь

а Λ_i, 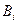удовлетворяют рекуррентным соотношениям

при граничных условиях

Представленные формулы определяют алгоритм управления с точ­ностью до знания матриц . Уточнение последних может быть про­изведено методом последовательных приближений для осредненнои в статистическом смысле траектории процесса перевода: с использованием найденного алгоритма управления (5.72). Элементы , входящие в мат­рицы в начальном приближении, могут быть заданы, например, равными . В каждом последующем приближении они уточняются на основе моделирования осредненного процесса. Опи­санный метод можно трактовать как простейшую разновидность метода статистической линеаризации. При необходимости статис­тическая линеаризация величины щх% может быть проведена и обычным способом, который, однако, является более громоздким.

Определив структуру управления, а следовательно, синтезируе­мую составляющую, можно перейти ко второму этапу оптимизации, т. е определению целочисленной последовательности .

В первом приближении эту задачу можно решить, используя для оценки критерия оптимальности квадратичную функцию будущих потерь . В этом случае последовательность определится из условия минимизации величины

по всем , с учетом ограничений . Так как все — целые числа, то для решения задачи следует использовать прямые методы поиска.

Уточнение полученной таким образом последовательности может быть проведено путем минимизации величины /, най­денной более точными методами, например, методом статистическо­го моделирования процесса перевода с использованием модели (5.71) и алгоритма (5.72). В этом случае оценка обобщенного кри­терия имеет вид

где — величина, характеризующая обобщенный критерий опти­мальности в j-й реализации; n — число реализаций.

При использовании метода статистического моделирования не­трудно получить оценки и других характеристик процесса перевода, в частности, характеристики конечной точности

где — величина в j-й реализации.

Решение задачи завершается отыскиванием множителя Лагранжа 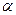в обобщенном критерии оптимальности из условия .