Оптимальное управление линейной стохастической системой
Проиллюстрируем возможность применения достаточных условий оптимальности для решения задачи синтеза на примере управления линейной стохастической системой вида
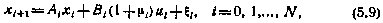
где 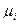 — центрированная случайная величина с дисперсией
— центрированная случайная величина с дисперсией  , характеризующая ошибки реализации управляющего (корректирующего) воздействия, пропорциональные величине этого воздействия, так называемое мультипликативное возмущение;
, характеризующая ошибки реализации управляющего (корректирующего) воздействия, пропорциональные величине этого воздействия, так называемое мультипликативное возмущение; 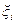 — центрированный случайный вектор с корреляционной матрицей
— центрированный случайный вектор с корреляционной матрицей 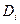 , характеризующий воздействия, не зависящие от величины управления, так называемое, аддитивное возмущение. В качестве критерия оптимальности примем ожидаемое значение обобщенной характеристики, равной взвешенной сумме энергетических затрат и конечной точности:
, характеризующий воздействия, не зависящие от величины управления, так называемое, аддитивное возмущение. В качестве критерия оптимальности примем ожидаемое значение обобщенной характеристики, равной взвешенной сумме энергетических затрат и конечной точности:
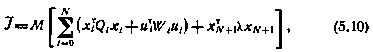
где 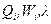 — заданные матрицы.
— заданные матрицы.
Рекуррентное соотношение (5.7) для данной задачи принимает вид
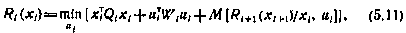
причем согласно (5.8) в конечный момент
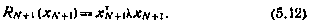
Для момента i — N с учетом (5.9) получаем
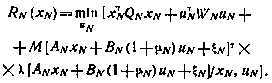
Раскроем в последнем выражении операцию математического ожидания. Получим
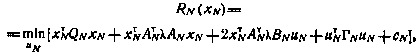
где

Полагая, что матрица 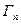 — положительно определенная, находим алгоритм оптимального управления для момента i = N:
— положительно определенная, находим алгоритм оптимального управления для момента i = N:
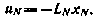
Здесь
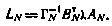
С учетом найденного алгоритма управления выражение для функции 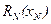 может быть преобразовано к виду
может быть преобразовано к виду
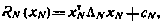
где через ΛN обозначена матрица
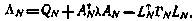
По индукции нетрудно убедиться, что функция будущих потерь 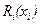 для любого момента i при определенных предположениях о матрицах
для любого момента i при определенных предположениях о матрицах 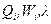 представима в виде
представима в виде

Действительно, предполагая, что (5.13) имеет место в момент i+1, т.е.
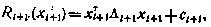
на основе рекуррентного соотношения (5.11) получаем соотношение (5.13), причем Λi, 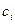 оказываются связанными с Λi+1,
оказываются связанными с Λi+1, 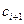 соотношениями
соотношениями
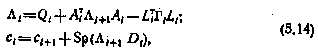
где
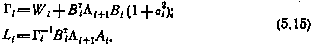
Попутно получаем и алгоритм оптимального управления в виде

Алгоритм (5.15) минимизирует правую часть в выражении (5.11), если матрицы 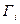 - оказываются положительно определенными. Можно показать, что для этого достаточно потребовать положительную определенность матрицы
- оказываются положительно определенными. Можно показать, что для этого достаточно потребовать положительную определенность матрицы 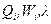 .
.
Из равенства (5.12) получаем граничные условия для матрицы Λi и коэффициента 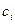 :
:

Таким образом, алгоритм оптимального управления линейной стохастической системой (5.9) при квадратичном критерии (5.10) является линейным. В общем случае коэффициенты обратной связи, определяемые матрицей 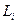 , зависят от статистических свойств мультипликативного возмущения
, зависят от статистических свойств мультипликативного возмущения 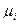 . Если же
. Если же 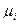 отсутствует, т. е.
отсутствует, т. е. 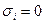 , то нетрудно заметить, что матрица коэффициентов обратной связи
, то нетрудно заметить, что матрица коэффициентов обратной связи 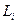 оказывается инвариантной по отношению к возмущениям. Итак, при наличии только аддитивных возмущений алгоритм оптимального управления линейной стохастической системой (5.9) полностью совпадает с оптимальным алгоритмом управления соответствующей детерминированной системой, аддитивные возмущения сказываются лишь на значении функции будущих потерь и, следовательно, на величине критерия оптимальности. Наличие же мультипликативных возмущений приводит к изменению оптимального Управления (в данном случае не самой структуры, а лишь ее параметров
оказывается инвариантной по отношению к возмущениям. Итак, при наличии только аддитивных возмущений алгоритм оптимального управления линейной стохастической системой (5.9) полностью совпадает с оптимальным алгоритмом управления соответствующей детерминированной системой, аддитивные возмущения сказываются лишь на значении функции будущих потерь и, следовательно, на величине критерия оптимальности. Наличие же мультипликативных возмущений приводит к изменению оптимального Управления (в данном случае не самой структуры, а лишь ее параметров 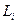 ).
).
