Численные методы программирования оптимального управления

В связи с тем, что задача программирования оптимального управления стохастической дискретной системой в общем случае может быть интерпретирована как специальная задача ма­тематического программирования, для ее численного решения мо­гут быть применены и соответствующие методы [28].

Ниже обсуждаются особенности применения для этой цели 'наи­более распространенных методов математического программирова­ния, таких, как градиентные методы и методы второго порядка.

Градиентные методы при отсутствии ограничений.Обратимся снова к задаче оптимизации программы управления системой

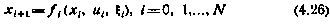
с целью минимизации терминального критерия

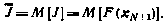
Как и прежде, считается, что начальное состояние х₀ известно. Предположим сначала, что ограничения на вектор управления отсутствуют.

Не стремясь здесь к получению точного решения с использова­нием условий оптимальности, рассмотрим процедуру приближен­ного решения задачи методом последовательных приближений, ос­нову которого составляет градиентный метод поиска.

Обозначим через , , 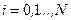q-e приближение иско­мой последовательности. Тогда в соответствии с градиентным ме­тодом [28] новое (q+1)-е приближение может быть найдено спо­мощью соотношения

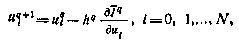
где 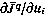— градиент критерия оптимальности по вектору 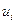на q-й итерации; 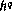— шаг поиска.

Смысл данного соотношения заключается в том, что новое при­ближение управления 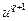получается путем перехода из старого приближения 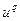в направлении антиградиента 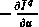с шагом .

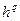Такое направление поиска, как известно, является локально наи­лучшим. В этом направлении минимизируемая функция имеет наи­большую скорость убывания.

Составляющие градиента 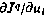могут быть определены чис­ленными методами как отношение приращения критерия 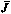к мало­му приращению (пробному) соответствующей составляющей управления .

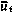Однако при таком подходе возникают настолько значительные вычислительные трудности, особенно при больших числах N и раз­мерностях твектора управления 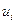,что возможность получения решения становится сомнительной. Указанные трудности сущест­венно сокращаются, если обратиться к методу сопряженных си­стем. Напомним, что согласно этому методу вычисление градиента 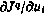может быть осуществлено по формуле

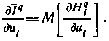
Здесь через 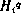обозначен гамильтониан на q-й итерации, равный

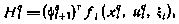
где в свою очередь вектор 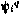удовлетворяет сопряженной системе

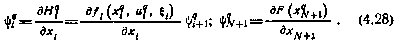
Из приведенных соотношений видно, что для вычисления градиен­тов 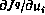на каждой итерации необходимо вычислить математи­ческое ожидание производной гамильтониана по вектору управле­ния 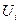. А это может быть осуществлено путем совместного ста­тистического моделирования исходной системы (4.26) и сопряжен­ной (4.28).

Алгоритм такого моделирования состоит в следующем. С помо­щью датчика случайных чисел формируется конкретная j-я реали­зация последовательности случайных векторов 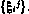, 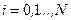. Далее при заданном начальном условии х₀ и известном управле­нии на q-итерации согласно (4.26) моделируется в прямом време­ни при изменении i от 0 до N j-я реализация фазовой траектории

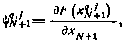
Определив фазовый вектор в конечный момент 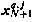и вычислив граничное значение сопряженного вектора

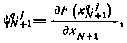
можем промоделировать и сопряженную систему в соответствии с(4.28):

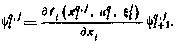
Зная сопряженный вектор в j-й реализации, согласно можно вычислить градиент критерия в данной реализации:

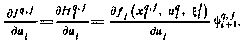
Если теперь произвести осреднение по всем реализациям, то по­лучим градиент исходного критерия оптимальности по управлению 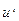на q-й итерации:

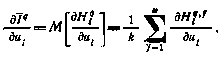
Здесь через k обозначено количество реализаций.

Основное преимущество метода сопряженных систем состоит в том, что в процессе моделирования для вычисления значения кри­терия оптимальности 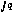и набора градиентов 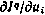для всех мо­ментов 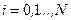в каждой реализации достаточно лишь один раз обратиться к системе (4.26) в прямом времени и к системе (4.28) - в обратном времени.

С целью улучшения процесса сходимости рассматриваемого градиентного метода при моделировании целесообразным оказы­вается применение зависимых испытаний, точнее, использование одних и тех же реализаций случайных векторов 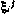, , 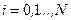на всех итерациях градиентного поиска. Такой способ моделирования является более экономичным, так как в конечном счете позволяет ограничиться существенно меньшим числом реализаций, чем при использовании независимых испытаний [26].

Шаг поиска 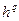может быть выбран различными способами. На­пример, при реализации простейшего градиентного метода он при­нимается постоянным, 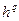=const. При реализации метода наиско­рейшего спуска шаг 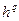выбирается наилучшим на данной итера­ции, т. е. из условия достижения критерием своего наименьшего значения в направлении антиградиента:

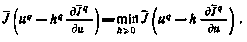
Учет ограничений на компоненты вектора управления.Часто в

задачах управления ограничения, накладываемые на компоненты 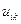вектора управления 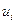, имеют вид

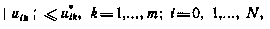
где через 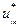обозначено предельное значение компоненты .

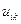В этих случаях для поиска может быть использована следую­щая модификация градиентного метода, являющаяся по сути де­ла реализацией проективного градиентного метода [28].

Если точка 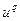является внутренней точкой допустимого множе­ства U или граничной, но с градиентом, направленным внутрь допустимого множества U, то переход к новому приближению 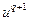осуществляется в соответствии с обычной схемой

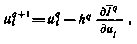
где градиент 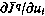вычисляется по-прежнему согласно (4.27). Однако выбор шага поиска теперь следует проводить с учетом до­полнительного ограничения

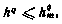
где через 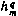обозначен максимально возможный на q-й итерации шаг поиска. Для его определения найдем сначала предельное зна­чение шага поиска 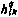, если принять во внимание только ограни­чения на компоненту управления :

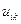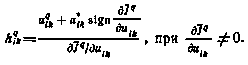
Тогда 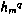с учетом всех ограничений будет равен

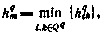
где через 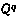обозначено множество индексов i, k, для которых 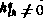. Заметим, что равенство 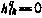означает, что компонента 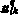принимает свое предельное значение, а градиент 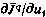направлен во вне множества U.

Если множество 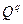окажется пустым, то это будет означать, что точка 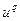является граничной, а градиент направлен во вне до­пустимой области U. В этом случае переход к новому приближе­нию естественно осуществить по следующей схеме:

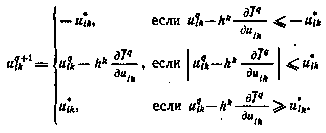
Смысл данной схемы состоит в том, что если при движении вдоль антиградиента какая-либо компонента вектора управления не выходит за пределы допустимого множества, то новое приближение по этой компоненте определяется согласно градиентному методу, если же при таком движении происходит выход за допус­тимое множество, то значение компоненты принимается равным прежнему предельному значению.

Оптимизация программы проведения однопараметрической коррекции.Проиллюстрируем возможность, применения изложен­ного метода на задаче оптимизации программы проведения однопараметрической коррекции космического аппарата. В качестве математической модели процесса коррекции, как и прежде, примем скалярное конечноразностное уравнение

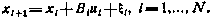
Будем считать, что имеют место соотношения (4.16).

Требуется определить последовательность корректирующих воздействий 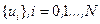, обращающих в минимум терминаль­ный критерий

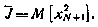
В отличие от рассмотренного ранее случая полагаем, что «а каждое корректирующее воздействие накладывается ограничение .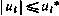

Для получения точного решения задачи следовало бы восполь­зоваться необходимыми условиями оптимальности в форме диск­ретного принципа минимума. При этом задача оптимизации све­лась бы к некоторой краевой задаче, трудности решения которой обсуждались в предыдущем разделе. Если же получение точного решения не требуется, то для получения приближенного решения можно использовать изложенный выше градиентный метод. Вычис­лительный алгоритм такого метода в данном случае может быть представлен следующим образом.

1. Задается любое допустимое управление — начальное при­ближение .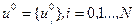

2. Переход от произвольного q-го приближения к новому (q+1)-му осуществляется по схеме

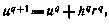
где 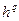— шаг поиска, а вектор 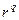определяет направление поиска на q-й итерации.

3. Определение вектора 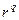на q-й итерации предполагает вы­полнение следующих операций:

1) определяется производная 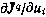на q-й итерации.

Так как в данном случае гамильтониан равен

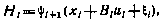
то согласно (4.27) и (4.28) имеем

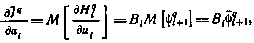
причем

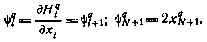
Отсюда следует, что математическое ожидание сопряженной пере­менной для всех моментов времени есть величина постоянная и равная

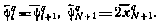
Математическое ожидание конечного промаха 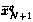в свою очередь может быть найдено на основании исходной модели движения

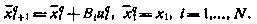
Заметим, что в силу линейности модели в данном случае при определении производных 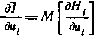статистического моделирования проводить не требуется;

2) вычисляется максимально допустимый шаг поиска на q-й итерации согласно соотношениям

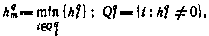
где

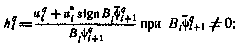
3) формируются компоненты вектора 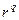, определяющего на­правление поиска на q-й итерации:

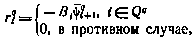
4) выбор шага поиска hi можно осуществить наилучшим обра­зом, т. е. из условия

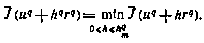
Причем характерно, что для вычисления значения самого кри­терия 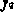на q-й итерации можно воспользоваться уравнением для' второго момента 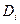текущего промаха 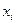, которое имеет вид

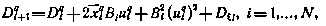
с граничным условием 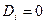. При i = N+1 получаем .

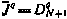Таким образом, в данной задаче удается избежать статистиче­ского моделирования на всех этапах поиска.

Применение методов второго порядка. Наиболее существенным недостатком всех градиентных методов (особенно при решении за­дач большой размерности) является медленная сходимость про­цесса поиска. В стохастических задачах, где в общем случае для вычисления как самой минимизируемой функции, так и ее произ­водных на каждой итерации должно производиться статистическое моделирование, этот недостаток еще более усугубляется. Одним из способов улучшения сходимости процесса поиска является учет при формировании нового приближения вторых производных кри­терия оптимальности, другими словами, использование методов второго порядка. Простейшим среди этих методов является метод Ньютона.

Его суть состоит в том, что в качестве нового (q+1)-го приближе­ния принимается оптимальное решение, обеспечивающее минимум квадратичной аппроксимации критерия оптимальности 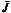на q-м приближении. Итак, квадратичная аппроксимация, получаемая путем разложения критерия 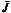в ряд Тейлора в окрестности q-го приближения, имеет вид

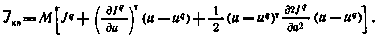
Произведя обычную минимизацию по вектору и путем приравни­вания нулю градиента 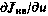, получаем

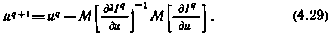
Предполагается, естественно, что ограничения на управления отсутствуют, а матрица 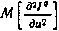положительно определенная, что обеспечивает, с одной стороны, существование обратной матрицы, а с другой стороны, гарантирует достижение в точке 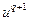миниму­ма .

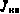Покажем, что вычисление матриц вторых частных производных в каждой реализации может быть осуществлено, как и вычисление составляющих градиента при использовании сопряженных систем, путем однократного обращения к некоторой системе уравнений.

С этой целью продифференцируем дважды терминальный кри­терий 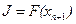по текущему управлению 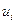. Дифференцируя в свое время этот критерий один раз, получали следующие соотно­шения, справедливые для каждой реализации:

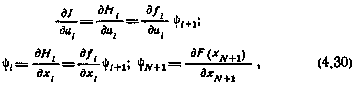
где

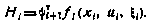
Для определения элементов матрицы вторых частных производ­ных продифференцируем 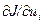еще один раз по .

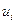Учитывая при этом (4.30), получим следующее соотношение:

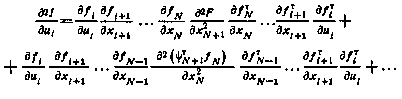
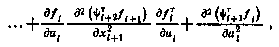
которое можно представить в более компактном виде

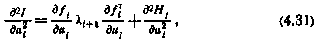
если ввести в рассмотрение обозначения

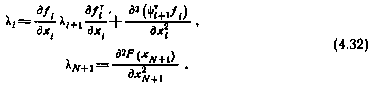
Аналогично для матрицы смешанных производных в предполо­жении j>i будем иметь

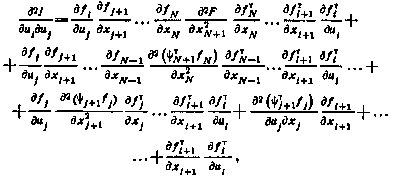
или в компактной форме

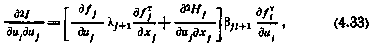
где 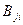— матрицы, удовлетворяющие рекуррентному соотношению

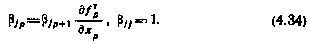
Таким образом, на основании соотношений (4.31) — (4.34) с граничными условиями на правом конце путем однократного про­счета в обратном времени можно получить значения всех элемен­тов матрицы вторых частных производных 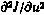в конкретной реа­лизации. Используя далее метод статистического моделирования по описанной ранее схеме и произведя осреднение по совокупности реализаций, получаем матрицу 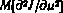в алгоритме (4.29).

Хорошо известно [28], что метод Ньютона, имея большую скорость сходимости, чем градиентные методы, обладает лишь локальной сходимостью. Это значит, что метод обеспечивает сходимость процесса поиска к оптимальному решению при условии выбора достаточно хорошего начального приближения. В противном слу­чае метод может оказаться расходящимся. Для придания методу свойства глобальной сходимости по аналогии с градиентными ме­тодами вводят шаг поиска на каждой итерации 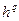, и схема, теперь уже модифицированного метода Ньютона, принимает вид

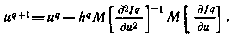
Шаг поиска может выбираться разными способами, например, из условия

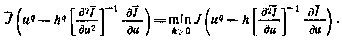
Естественно, что при больших числах N, а значит, и при боль­ших размерностях вектора и вычисление полной матрицы может потребовать значительных затрат машинного времени. Для их сокращения можно рекомендовать использование приема погрупповой оптимизации, согласно которому последующее приближение получается из предыдущего варьированием компонент вектора уп­равления лишь в один единственный i-й момент времени при фик­сированных значениях управлений в другие моменты. Затем после­довательно варьируются и другие векторы. При такой погрупповой оптимизации алгоритм (4.29) принимает вид

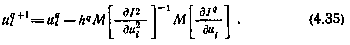
Простота данного алгоритма состоит в том, что он не требует вычисления матриц вторых смешанных производных 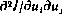, , 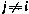с которыми и связаны основные вычислительные трудности. Вычисление матриц 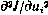не вызывает затруднений.

Иногда может оказаться полезным и другой, еще более простой алгоритм поиска, предполагающий, что матрица 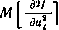яв­ляется диагональной. В этом случае для каждой j-й компоненты 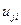вектора 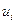получаем следующую расчетную формулу:

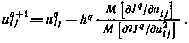
С одной стороны, как только что было установлено, этот алго­ритм может рассматриваться как частный случай модифицирован­ного метода Ньютона. С другой стороны, он может интерпретиро­ваться как одна из разновидностей градиентных методов, в кото­рой поиск осуществляется в пространстве управлений с перемен­ной на каждой итерации метрикой.

Параметрическая оптимизация закона коррекции.Проиллюст­рируем применение методов второго порядка снова на задаче, свя­занной с оптимизацией процесса коррекции космического аппара­та путем определения коэффициентов обратной связи 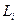в зависи­мости .

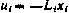Как и прежде, математическую модель процесса коррекции и критерий оптимальности представим в виде

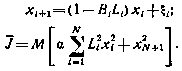
Сначала преобразуем данную задачу к задаче терминального управления. С этой целью введем вспомогательную переменную 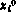, определив ее с помощью уравнения

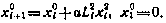
Тогда критерий оптимальности становится терминальным в прост­ранстве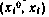

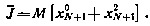
Теперь для решения задачи обратимся к алгоритму (4.35). В дан­ном случае гамильтониан имеет вид

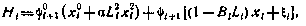
а сопряженные переменные 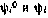удовлетворяют уравнениям

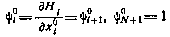
и

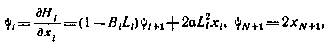
откуда следует, что

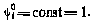
Как и прежде, производная критерия оптимальности 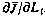, равная согласно (4.30)

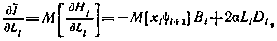
может быть приведена к виду

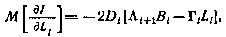
где 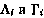определяются согласно (4.23) - (4.25) , а второй момент 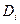согласно соотношению

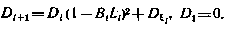
Найдем теперь выражение для второй производной 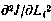. Рас­крывая (4.31), с учетом (4.32) в данном случае можно получить

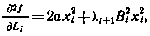
где 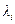определяется с помощью рекуррентного соотношения

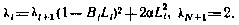
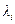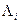Нетрудно заметить, что матрицы и связаны условием

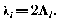
Учитывая это, получаем

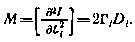
Анализируя полученные выражения, можно установить, что 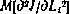не зависит от текущего параметра 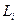, хотя зависит от всех последующих 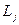при j>i.

Поэтому целесообразно оптимизацию по отдельным компонен­там искомой последовательности проводить в такой очередности: j =N, N—1, ..., 1. Оказывается, что применение алгоритма (4.35) в этом случае позволяет за один цикл итераций по всем 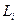, i = N, ..., 1, найти сразу точное решение задачи. Действительно, получаем

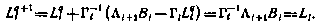
Учитывая данный результат, можно рекомендовать и при реше­нии более сложных задач, в частности, при оптимизации нелиней­ных систем погрупповой поиск управляющих воздействий осуще­ствлять в очередности j = N, N-1, ..., 1.

НЕОБХОДИМЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ ДЛЯ НЕПРЕРЫВНОГО СЛУЧАЯ. НЕПРЕРЫВНЫЙ ПРИНЦИП МИНИМУМА (МАКСИМУМА)

Решение задач, связанных с оптимизацией непрерывных как стохастических, так и детерминированных систем, практически всегда требует дискретизации. Можно указать два подхода к такой дискретизации.

Первый состоит в переходе от исходной непрерывной задачи к дискретной сразу до ее решения. При этом дифференциальные уравнения, описывающие поведение системы, заменяются конеч­но-разностными. Соответствующим образом преобразуется и кри­терий оптимальности. Для решения полученной вновь задачи мо­гут быть применены либо условия оптимальности для дискретных систем, либо соответствующие численные методы поиска опти­мального управления.

Второй подход связан с использованием необходимых условий оптимальности, полученных непосредственно для исходной непре­рывной задачи. Эти условия в явном виде редко позволяют полу­чить решение задачи оптимизации. Они обычно лишь трансформи­руют исходную задачу в некоторую другую, например связанную с решением краевой задачи для системы дифференциальных урав­нений, при решении которой в конечном счете приходится прово­дить также дискретизацию.

Заранее бывает трудно отдать предпочтение какому-либо од­ному из этих подходов. Первый подход, очевидно, более прост в реализации при получении численного решения задачи, обладает определенной универсальностью, так как фактически исходную за­дачу сводит ,к специальной задаче .математического программиро­вания, для решения которой в настоящее время накоплен богатый опыт. Однако применение второго подхода иногда позволяет более просто выявить структуру оптимального управления, а в некото­рых случаях и найти более эффективный способ решения задачи в целом.

Учитывая это, рассмотрим необходимые условия оптимально­сти в задаче программирования оптимального управления непре­рывной стохастической системой и их применение для решения конкретных задач.

Пусть динамическая система на интервале времени [0, Т] опи­сывается следующим стохастическим дифференциальным уравне­нием

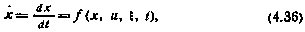
где x=x(t), u = u(t) —векторы состояния и управления соответст­венно в текущий момент, 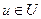,U — множество допустимых управ­лений; 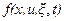—вектор-функция, непрерывно дифференцируемая по своим аргументам; 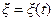—случайный процесс; с извест­ными статистическими характеристиками.

Задача программирования оптимального управления заключа­ется в отыскании такой временной зависимости u(t), которая обеспечивает перевод системы (4.36) из заданного начального состояния х(0)=х₀ в некоторое конечное состояние х(Т) с мини­мальным значением критерия

Наиболее просто необходимые условия оптимальности для сфор­мулированной задачи получаются в предположении, что непрерыв­ные случайные процессы 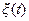и x(t) могут быть представлены в виде дискретных последовательностей случайных векторов 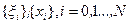, которые при стремлении интервала дискретности Δ к нулю стягиваются к исходным процессам 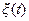и x(t). В этом слу­чае для малых Δ (с точностью до членов первого порядка малости) вместо уравнения (4.36) и критерия (4.37) можно записать их ко­нечно-мерные аналоги

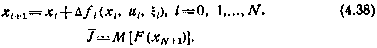
Исходная задача, таким образом, в первом приближении оказыва­ется эквивалентной задаче программирования оптимального уп­равления 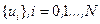, изученной нами ранее. Поэтому для нее необходимые условия оптимальности можно выписать. С этой целью составим гамильтониан для этой задачи, обозначая его че­рез :

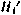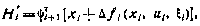
где сопряженный вектор 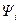удовлетворяет при этом уравнению

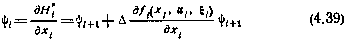
при граничном условии

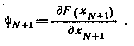
Тогда, если 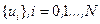— оптимальная последовательность, то согласно (4.10) имеют место следующие условия:

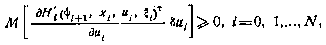
для всех допустимых 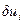т. е. удовлетворяющих условию .

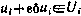Смысл этих условий состоит в неотрицательности вариации 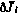терминального критерия 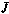, получаемой за счет вариации управле­ния 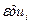в i-й момент:

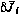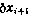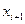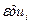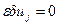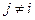Установим связь вариации с вариацией фазового вектора , вызываемой в свою очередь вариацией управления . С этой целью примем, что вариации управления во все другие мо­менты времени, кроме i-го, равны нулю, т. е. при , а 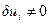. Тогда для моментов 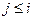вариация 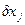вектора 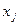будет тождественно равна нулю. Для момента j = i+1 в соответствии с уравнением (4.38) будем иметь

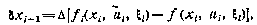
а для моментов j>i+l вектор 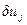удовлетворяет уравнению в отк­лонениях

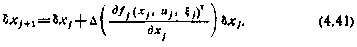
Здесь через 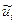обозначено любое допустимое управление 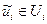в отличие от оптимального управления .

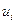Покажем, что скалярное произведение вектора 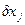, определя­емого уравнением (4.41), и сопряженного вектора 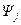, определяемо­го в соответствии с (4.39), представляет собой постоянную величи­ну для любых 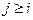. Действительно, согласно (4.39) и (4.41)

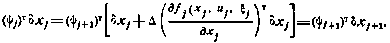
Но для момента j = N+1 согласно (4.38), (4.39) математическое ожидание этого произведения определяет вариацию критерия оп­тимальности

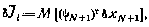
которая должна быть неотрицательной. Поэтому условие опти­мальности (4.40) можно представить так:

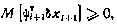
или, раскрывая вариацию 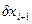вектора 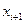, в развернутом виде

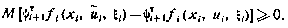
Полученное соотношение, как уже было установлено, справедливо для любого допустимого управления 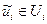и для любого момента времени 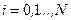. Если теперь ввести в рассмотрение новый га­мильтониан в виде

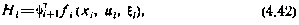
то условию оптимальности можно придать следующий вид:

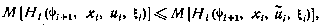
или окончательно

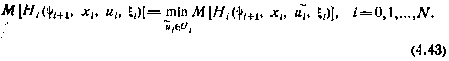
Таким образом, для дискретной системы (4.38) при малых зна­чениях интервала дискретности оказывается справедливым диск­ретный принцип минимума по отношению к гамильтониану (4.42) независимо от свойства гамильтониана и допустимого множе­ства .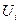

Осуществим теперь предельный переход во всех соотношениях, определяющих необходимые условия оптимальности. Для этого устремим интервал дискретности Δ к нулю. Соотношения (4.38) примут вид исходного дифференциального уравнения (4.36) и ис­ходного критерия (4.37), а конечно-разностное уравнение (4.39) для сопряженного вектора 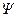перейдет в дифференциальное урав­нение

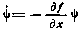
с граничным условием

Необходимые условия оптимальности (4.43) примут вид непрерыв­ного принципа минимума

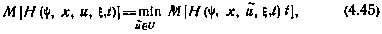
где гамильтониан

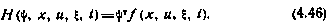
Смысл условия (4.45) заключается в том, что при оптимальном управлении в каждый момент времени математическое ожидание гамильтониана достигает своего минимального (по управлению) значения. С учетом вида гамильтониана (4.46) уравнение для со­пряженного вектора можно записать в виде

Благодаря принципу минимума (4.45), исходная задача определе­ния оптимальной программы управления u(t) из условия миними­зации функционала (4.37) редуцируется к краевой задаче для си­стемы стохастических уравнений (4.36) и (4.47). Для исходных уравнений (4.36) граничное условие x(0) задано «слева», т. е. в на­чальный момент, а для сопряженных уравнений (4.47) — «спра­ва», т. е. в конечный момент времени в виде условия (4.44). Опти­мальное управление должно удовлетворять этим краевым условиям и одновременно обращать в минимум математическое ожидание га­мильтониана.

Если, как и при рассмотрении дискретного случая, в качестве граничного условия для сопряженного вектора принять условие 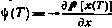, т. е. изменить в условии (4.44) знак на обратный, то необходимое условие оптимальности (4.45) примет более при­вычную форму принципа максимума:

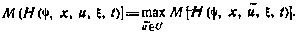
Если в исходной задаче критерий оптимальности имеет более сложную интегротерминальную структуру вида

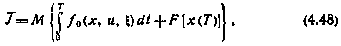
то путем введения дополнительной переменной 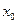, определяемой с помощью дифференциального уравнения

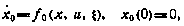
критерий (4.48) сразу сводится к терминальному виду

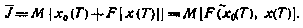
по отношению к вектору состояния х и дополнительной переменной 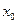совместно.

Составим гамильтониан для данной расширенной задачи:

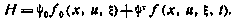
Здесь сопряженная компонента 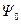удовлетво