Метод максимума правдоподобия при нормальном распределении ошибок измерений

Пусть вектор подчиняется нормальному закону рас­пределения с нулевым математическим ожиданием и диагональной корреляционной матрицей . В таком случае

С учетом (3.177), (3.178) получаем функцию правдоподобия:

Исследуем функцию правдоподобия на максимум, следуя [6]. Пе­репишем (3.179) в виде

где через С обозначен множитель перед экспонентой, не завися­щий от y^N и а.

Поскольку функция L(y^N, а) всюду не отрицательна, то для нее существует логарифм, а так как логарифм — монотонная функция, то максимум ln L(y^N, а) совпадает с максимумом L(y^N, а).

Поэтому исследуем на максимум In L (y^N, a):

Из (3.180) следует, что максимум ln L(y^N, а) достигается при ми­нимуме по а положительно определенной квадратичной формы

Поэтому имеем

Это уравнение совпадает с (3.138) при . Отсюда следует, что метод наименьших квадратов можно рассматривать как част­ный случай метода максимума правдоподобия: при аддитивных и независимых ошибках измерений, подчиняющихся нормальному закону распределения, оценки, получаемые по методу наименьших квадратов, определяются из тех же условий, что и оценки макси­мального правдоподобия. Поэтому все алгоритмы оценивания и ре­зультаты, касающиеся метода наименьших квадратов, приведен­ные выше, справедливы и в данном случае. С другой стороны, при­веденные в данном разделе рассуждения можно рассматривать как теоретическое обоснование тех условий, когда оценки, полученные по методу наименьших квадратов, будут обладать свойствами оце­нок максимального правдоподобия, т. е. будут состоятельными.

При нахождении оценок максимального правдоподобия так же, как и при использовании метода наименьших квадратов, может учитываться дополнительная информация, содержащаяся в апри­орной плотности вероятностей вектора оцениваемых параметров, если таковая имеется в нашем распоряжении [37]. Пусть задана априорная плотность вероятностей вектора а. В соответствии с формулой Байеса (1.9) имеем

где

В этой формуле p(a/y^N) —апостериорная плотность вероятно­стей вектора а. Как указывалось в разд. 3.1, метод максимума апостериорной вероятности заключается в выборе в качестве оцен­ки такого значения вектора а, при котором достигается макси­мум p(a/y^N).

Так как множитель C₁ в правой части (3.182) не зависит от а, то задача сводится к отысканию максимума функции p₀(a)p(y^N/a)=p₀(a)L(y^N/a). Необходимые условия экстремума по а этой функции имеют вид

Уравнение (3.183) отличается от условия первым слага­емым, учитывающим имеющуюся априорную информацию. Необ­ходимые условия (3.183) приводят к системе нелинейных алгебра­ических уравнений относительно а, которые необходимо решать численными методами.

Пусть априорная плотность вероятностей p₀(а) определяет не­которую априорную оценку вектора а, которую обозначим ; ошиб­ку априорной оценки обозначим . Тогда p₀(а) = p₀(а- ) = = p₀( 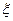). В то же время имеем L(y^N, a)=p(y^N/a)=p[y^N- 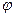(a)]. В результате получаем p₀(а)р(у^N/а)=р_а(а- ) p[y^N- 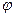(a)]. Это же выражение может быть получено непосредственно из определения функции правдоподобия L(y^N, a)=L[y^N- 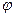(а)]. Для этого доста-

точно рассматривать компоненты вектора как дополнительные измерения и сформировать блочный вектор измерений в виде .

Тогда, считая ошибк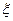и и независимыми, получаем функцию правдоподобия в виде

где — плотность вероятностей вектора .

Таким образом, метод максимума апостериорной вероятности представляет собой обобщение метода максимума правдоподобия при условии, что априорные оценки рассматриваются как допол­нительные измерения, а ошибки априорной оценки и ошибки изме­рений считаются независимыми.

Соответствующая модификация может быть осуществлена и в алгоритме наименьших квадратов. Эта модификация уже была ис­пользована в разд. 3.3.4. при построении аналитического алгорит­ма априорной оценки точности определения орбиты ИСЗ.

Вернемся к задаче отыскания максимума функции р₀(а)×p(y^N/a). Рассмотрим случай, когда векторы и а подчиняются нормальному закону распределения:

В таком случае

Для исследования на максимум функции p(a/y^N) перейдем к ее логарифму:

Максимум по а достигается при минимуме по а двух последних слагаемых в правой части (3.185). Вследствие положи­тельной определенности соответствующих квадратичных форм име­ем условие минимума в виде

Формула (3.186) совпадает с формулой для нахождения оценки по методу наименьших квадратов (3.138) при или максиму­ма правдоподобия (3.181) при условии, что вектор а рассматрива­ется как вектор дополнительных измерений, проведенных с точно­стью, определяемой элементами матрицы Р_о.

Таким образом, соотношение (3.186), определяющее оценки максимума апостериорной вероятности при нормальном законе распределения ошибок измерения и нормальной априорной плот­ности вероятностей оцениваемого вектора, можно рассматривать как соотношение, определяющее оценки метода наименьших квад­ратов или оценки максимума правдоподобия, вычисленные с уче­том априорной информации, содержащейся в Р₀(a).

ГЛАВА