Квазилинейный дискретный фильтр Калмана

При рассмотрении конкретных примеров использования фильтра Калмана сходимость оценок, получаемых с его помощью,. к истинным значениям компонент вектора состояния зависит от того, насколько точно линейные уравнения описывают поведение реальной динамической системы, рассматриваемой в конкретной, технической задаче.

Так как соотношения, связывающие вектор состояния и вектор» измерений, как правило, нелинейны, возникает необходимость в их линеаризации. Как показывает моделирование процесса оценива­ния, линеаризации этих соотношений в окрестности опорной траек­тории служит, как правило, причиной того, что фильтр Калмана-дает не пригодные для практических целей оценки, так как насту­пает упоминавшаяся выше так называемая «неустойчивость фильтра Калмана», когда при уменьшении апостериорного среднеквадратич­ного отклонения какой-либо компоненты вектора состояния оценка этой компоненты в конкретной реализации все более отличается от ее истинного значения.

С целью устранения недостатков линейного фильтра Калмана возникла необходимость в разработке его модификации, основанной на линеаризации нелинейных уравнений движения оцениваемой ди­намической системы и соотношений для измерений в окрестности: оценки, полученной на предыдущем шаге.

Такая модификация позволяет улучшить свойства оценок более-полным учетом нелинейных свойств оцениваемой динамической си­стемы и соотношений для измерений по сравнению с алгоритмом: оценивания, основанным на линеаризации в окрестности опорной, (невозмущенной) траектории. Рассмотрим вывод соотношений мо­дифицированного указанным образом фильтра Калмана, который в дальнейшем будем называть квазилинейным.

Пусть изменение состояния оцениваемой системы описывается разностным уравнением

где x_i -n-мерный вектор состояния системы в момент времени t_i, u_i —m-мерный вектор управления. Закон управления, т. е. способ-формирования вектора управления на основе оценок компонент-вектора x_i считается заданным; 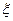—n-мерный вектор случайных возмущений. Относительно векторов x_i и предполагается, что при всех i они независимы и подчинены соответственно нормаль­ным законам распределения (3.14) и (3.15).

Вектор измерений у_i связан с вектором x_i соотношением

где у_i —l-мерный вектор измерений; g_i —l -мерная вектор-функция; η_i —l -мерный вектор независимых гауссовских ошибок измерений, подчиняющихся закону распределения (3.18).

В соотношении (3.91) вектор-функция g_i зависит не только от компонент вектора состояния x_i, но и от управления . Из последней записи следует, что вектор управления, переводящий систему из состояния i—1 в состояние i, формируется на основе байесовской оценки вектора , получен­ной в момент . В дальнейшем будем считать, что управление ре­ализуется без ошибок и фиксация в соответствующих плотно­стях вероятности эквивалентна фиксации т. е.

Так как разностное уравнение (3.90) и соотношение для измерений (3.91) нелинейны, то плотность вероятностей , определяю­щая байесовскую оценку , негауссовская. Запишем еще раз фор­мулу Байеса:

Учитывая независимость, аддитивность и гауссовость ошибок из­мерений, можем записать

Линеаризация соотношений (3.90) и (3.91) в окрестности опти­мальных оценок соответственно эквивалентна аппрокси­мации плотностей вероятностей тауссовскими распределениями.

В результате линеаризации соотношений (3,90) и (3.91) по и соответственно получаем

Из этих равенств следует, в частности, что

Плотности вероятностей с учетом линеариза­ции (3.90) и (3.91) имеют вид (3.28) и (3.29) соответственно. Плот­ность вероятностей p с учетом (3.94), (3.33) — (3.35), а так­же гауссовости, аддитивности и независимости запишется. в виде

.

В (3.97) матрица вычислена в точке . Подставляя выражения (3.28), (3.29), (3.97) в формулу (3.92), после преобра­зований, аналогичных тем, о которых говорилось в разд. 3.2.1, получаем следующее выражение для :

где

Соотношения (3.98), (3.99) совместно с соотношениями (3.95), (3.96) определяют квазилинейный дискретный фильтр Калмана. Начальные условия для квазилинейного фильтра совпадают с (3.46).

Заметим, что в соотношениях (3.95), (3.96), (3.98), (3.99) мат­рицы зависят не только от номера i, т. е. от момента времени, но и от соответствующих оптимальных оценок и вектора управления; соотношение (3.95) нелинейно. Поэтому при исполь­зовании квазилинейного фильтра Калмана матрица характе­ризующая точность вычисляемых оценок, не может быть вычислена заранее, отдельно от самой оценки и, следовательно, оценку точности, которая может быть получена с помощью этого алгорит­ма, следует проводить только путем имитационного моделирования процесса оценивания.

Приведенный алгоритм обеспечивает «устойчивую» фильтра-дию во многих случаях, когда линейный фильтр Калмана не позвс-.ляет добиться успеха. Причина такой устойчивости состоит в том, что с ростом размерности вектора , т. е. с увеличением объема об­рабатываемой информации и повышением точности оценок возможность линеаризации соотношений (3.90) и (3.91) в окрест­ности этих оценок становится все более обоснованной.