Исследование вынужденных вертикальных колебаний надрессорного строения подвижного состава

Колебания надрессорного строения происходят при непрерывном рассеивании энергии за счет гасителей колебаний и диссипативных свойств упругих элементов рессорного подвешивания. Это способствует быстрому затуханию колебаний и устраняет опасность перехода через резонансные зоны. Показатели виброзащиты подвижного состава оцениваются по максимальным значениям перемещений, ускорений и коэффициентов динамики.

Рис. 3.1. Динамическая модель колебательной системы вагона, локомотива с одной степенью свободы

Рассмотрим упрощенную динамическую модель вагона, локомотива с одной степенью свободы (рис. 3.1) при следующих основных допущениях [3]:

1) путь считается абсолютно жестким;

2) возмущения от неровностей пути считается детерминированными гармоническими.

Система имеет одну обобщенную координату В системе действуют следующие активные силы:

Fв- возмущающее силовое воздействие, зависящее от времени и задаваемое определенной зависимостью;

Fин= - сила инерции (где m- колеблющаяся масса неподрессоренного строения).

Делее будут приняты следующие обозначения;

- ускорение колебательного движения;

- диссипативная сила сопротивления колебаниям, создаваемая рессорным подвешиванием, имеющим жесткость ж (где 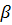- коэффициент затухания гасителя колебаний);

и - скорости вертикальных перемещений массы надрессорного строения m и массы колеса соотвественно при движении по волнообразной неровности рельсового пути.

Дифференциальное уравнение колебаний подпрыгивания надрессорного при возмущающем силовом воздействии и затухании можно представить следующим образом:

, (3.1)

Рассматривая систему как линейную,уравнение ее колебаний (3.1) преобразуем, введя параметры и n.

Здесь

- собственная частота колебаний недемфированной системы;

- относительно затухание колебаний.

Поскольку на вагон, локомотив действует кинематическое возмущение, то, принимая , уравнение колебаний его надрессорного строения примет вид

(3.2)

После решения уравнения (3.2), ряда преобразований в введения для дальнейшего анализа безразмерной частоты (где 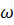- частота вынужденных колебаний системы) получим выражение для амплитудной частотной характеристики перемещений подпрыгивания или динамического коэффициента системы .

A(ξ)= . (3.3)

Динамический коэффициент показывает, во сколько раз амплитуда кинематического возмущения ŋ(t) увеличивает амплитуду колебаний надрессорного строения вагона z. Из уравнения (3.3) следует, что динамический коэффициент зависит от относительного затухания (демпфирования) n и соотношения частот вынужденных и собственных колебаний ξ. Динамический коэффициент имеет максимум на безразмерной частоте ξ=1, т. е. в области резонанса (когда ).

При движении по стыковому пути, вследствие удара колес о принимающий рельс, со стороны пути на вагоне возникают периодические силовые воздействия. От этих толчков происходят вертикальные колебания надрессорного строения.

Частота вынуждающих силовых воздействий

(3.4)

где - скорость движения;

- длина рельсового звена.

Явление резонанса наблюдается при . Тогда, с учетом выражения (3.4), скорость, при которой наблюдается явление резонанса при движении по стыковому пути, равна

(3.5)

Задача: Рассчитать и построить амплитудную частотную характеристику колебания подпрыгивания надрессорного строения вагона, локомотива с одноступенчатым рессорным подвешиванием, движущегося по стыковому пути, имеющему волнообразные неровности. Динамическую систему рассматривать как имеющую одну степень свободы, путь считать абсолютно жестким, а возмущения от неровности пути – детерминированными гармоническими. Определить также значение скорости движения, при которой может наблюдаться явление резонанса вертикальных колебаний надрессорного строения от силового внешнего возмущения, связанного с прохождением колесами стыков рельсового пути.

Таблица 3.1 – Исходные данные

Параметры	Номер варианта
Вес надрессорного строения вагона , Н/м
Жесткость рессорного подвешивания , Н/м
Относительное затухание колебаний n	0,1	0,1	0,15	0,15	0,2	0,2	0,25	0,25	0,3	0,3
Длина рельсового звена l, м	12,5	12,5	12,5	12,5	12,5

Вопросы на защиту:

1. Конструктивные связи: жесткие, упругие, упруго-вязкие, упруго-фрикционные.

2. Силовые характеристики упругих связей, упруго-вязких, упруго-фрикционных.

3. Жесткость, гибкость упругой связи.

4. Конструктивное устройство гидравлических гасителей колебаний, листовых рессор, фрикционных гасителей колебаний, пружин.

Практическая работа №4