Энтропия системы с непрерывным множеством состояний

Система называется непрерывной по данному описывающему ее параметру, если этот параметр является непрерывной величиной. Состояния такой системы нельзя перенумеровать: они непрерывно переходят одно в другое, причем каждое отдельное состояние имеет вероятность, равную нулю, а распределение вероятностей характеризуется некоторой плотностью 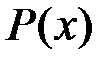. Например, генератор шума, напряжение на выходе которого может принимать любое значение, является непрерывной системой по указанному параметру.

Попытаемся ввести количественную меру неопределенности непрерывной случайной величины Х через энтропию 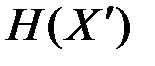дискретной случайной величины 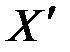, которая получается в результате квантования непрерывной величины Х по уровню. Математически квантование можно представить как нелинейное преобразование непрерывной величины Х. Вся область возможных значений величины Х разбивается на интервалы с длиной, равной 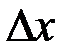. Каждому интервалу ставится в соответствие некоторое значение 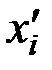, принадлежащее дискретному множеству .

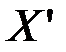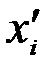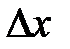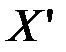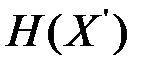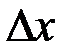Вероятность появления значения равна вероятности попадания случайной величины Х в соответствующий интервал. Чем меньше интервал квантования , тем точнее дискретная величина отображает свойства непрерывной величины Х. Поэтому в качестве количественной меры неопределенности случайной величины Х логично использовать значение энтропии при стремящимся к нулю:

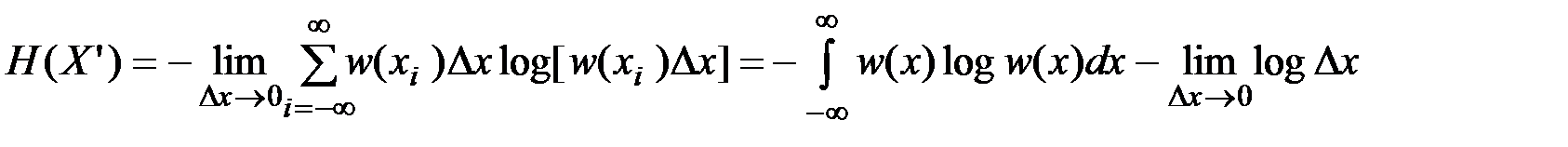
(4.11)

Первый член в (4.11) не зависит от 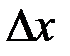- степени точности, с которой определяется состояние системы. От 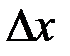зависит только второй член ( 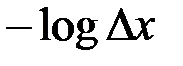), который стремится к бесконечности при 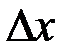,стремящимся к нулю. Это и естественно, поскольку, чем точнее мы хотим задать состояние системы, тем большую неопределенность мы должны снять.

Таким образом, мы убедились, что система с непрерывным множеством состояний не допускает введения конечной абсолютной меры неопределенности. Однако можно ввести количественную меру неопределенности указанной системы по отношению к другой непрерывной системе, состояния которой описываются случайной величиной Y с некоторым стандартным распределением. В качестве последнего (эталонного) удобно использовать равномерное в некотором интервале d распределение

.

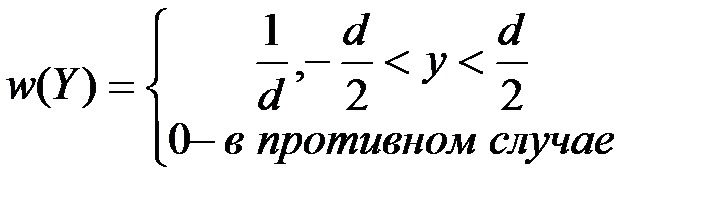Энтропия 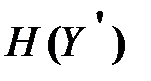вычисляется аналогично выражению (4.11)

.

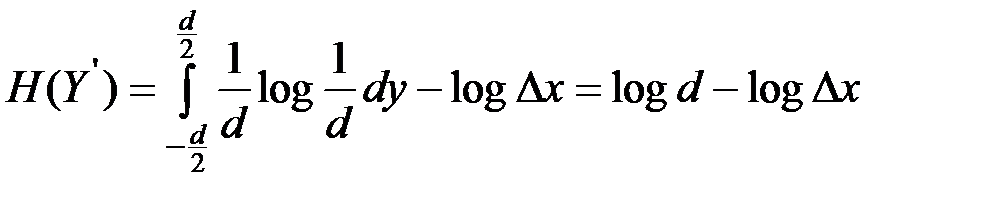Относительной (дифференциальной) энтропией случайной величины Х называется величина

.

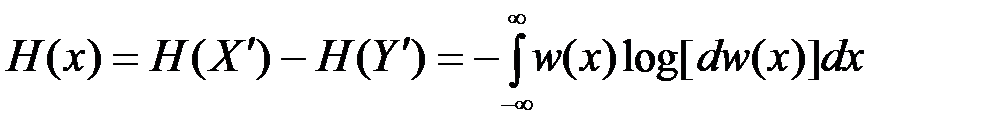В частности, если интервал d = 1, то

.

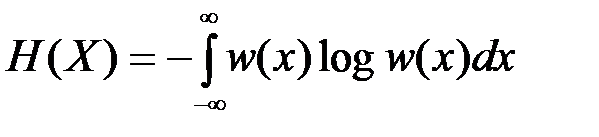Выясним физический смысл относительной энтропии .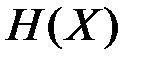

Пусть источник сообщений вырабатывает последовательность значений случайной величины Х. После квантования получим последовательность значений случайной величины :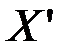

.

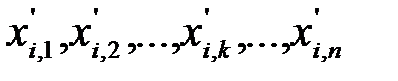При неограниченном увеличении длины последовательности с вероятностью, равной единице, появляются только типичные последовательности, число которых

,

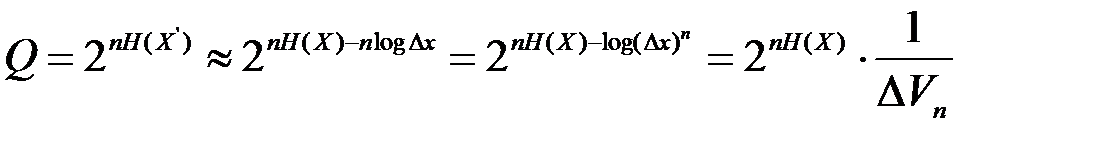где 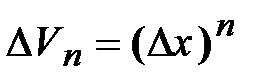- число элементарного n-мерного кубика. Конец вектора, изображающего типичную последовательность, является внутренней точкой этого кубика. Произведение 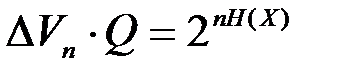равно объему некоторой области в n-мерном пространстве, внутренние точки которой изображают концы типичных векторов (последовательностей). При 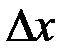, стремящихся к нулю, число типичных последовательностей стремится к бесконечности, объем каждого элементарного кубика стремится к нулю. При этом объем 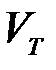, занимаемый типичными последовательностями, остается постоянным, равным .

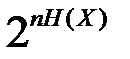Энтропию в дискретном случае можно было определить через число типичных последовательностей:

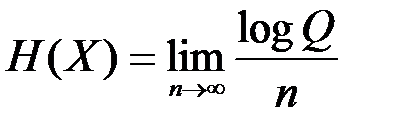
Аналогично относительную энтропию можно определить через объем 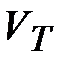, занимаемый типичными последовательностями:

.

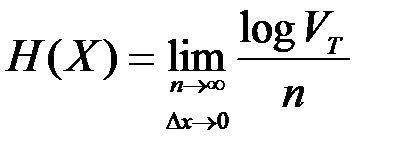В отличие от дискретного случая относительная энтропия может быть не только положительной, но и отрицательной, а также равной нулю. Чем больше объем 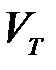, занимаемой типичными последовательностями, тем больше неопределенность того, какая из них появится. Единичному объему ( 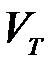=1) соответствует энтропия (неопределенность), равная нулю ( 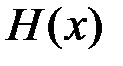=0). Это значение принимается за начало отсчета относительной энтропии.

В частности, относительная энтропия случайной величины с равномерным на единичном интервале (d = 1) распределением равна нулю:

.

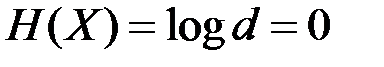В этом случае область n-мерного пространства, занимаемая типичными последовательностями, примерно совпадает с областью определения всех последовательностей и имеет форму куба единичного объема ( 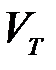= =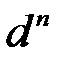1).