Дискретизация непрерывных сообщений и сигналов

Произвольную кусочно-непрерывную функцию 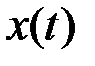, изображающую сообщение или сигнал, можно разложить в обобщенный ряд Фурье по полной системе ортонормированных функций:

,

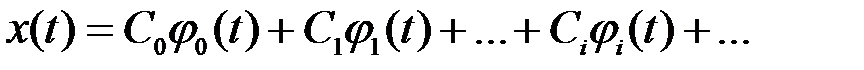если энергия функции 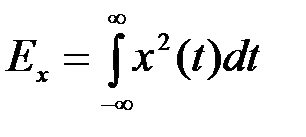конечна [9].

Бесконечная система действительных функций 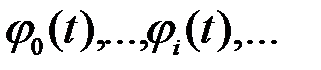называется ортогональной на отрезке [a, b], если

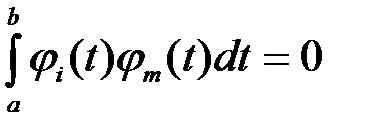при ,

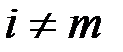а отдельная функция 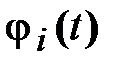называется нормированной, если

.

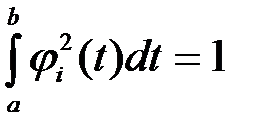Система нормированных функций, в которой каждые две различающихся функции взаимно ортогональны, называется ортонормированной системой. При аппроксимации функции 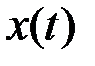ограничиваются, как правило, конечным числом членов ряда. При заданной системе функций 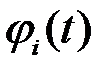и при фиксированном количестве членов ряда n значения коэффициентов 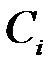можно выбрать такими, при которых среднеквадратичная ошибка аппроксимации

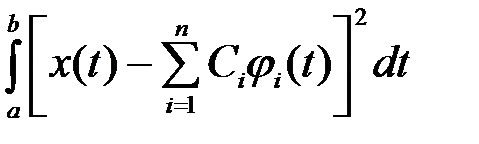
достигает минимума. Ряд, обеспечивающий минимум среднеквадратической ошибки называется рядом Фурье. Минимум среднеквадратичной ошибки достигается в том случае, когда коэффициенты ряда определяются по формуле

,

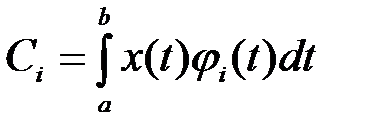при этом они вычисляются независимо друг от друга при любом значении n и называются коэффициентами Фурье.

Ряд, с определяемыми таким образом коэффициентами, называется обобщенным рядом Фурье.

Ортогональная система называется полной, если путем увеличения количества членов в ряде среднеквадратичную ошибку можно сделать сколь угодно малой.

Таким образом, по счетному множеству коэффициентов 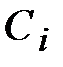можно с определенной точностью восстановить соответствующую функцию 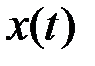можно заменить передачей последовательности коэффициентов 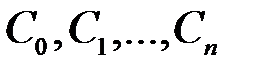. Указанную последовательность можно интерпретировать как вектор в n - мерном Евклидовом пространстве с координатами 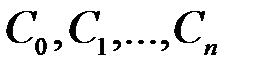, квадрат длины которого

.

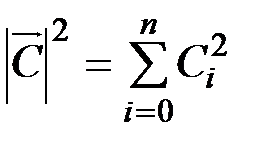Последнее равенство является обобщением теоремы Пифагора на случай n-мерного пространства. Путем непосредственных вычислений легко установить, что энергия сигнала

.

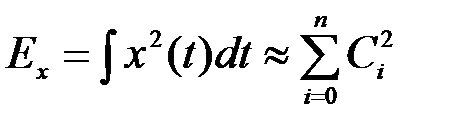Таким образом, дискретизацией называется замена непрерывной функции 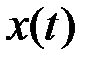, определенной на интервале, равном Т, последовательностью коэффициентов 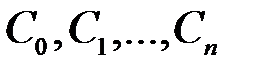... (вектором).

Выбор системы ортогональных функций 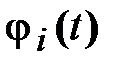определяется целью и физической сущностью решаемой задачи, а не чисто математическими умозаключениями.

С целью передачи сигнала по каналу связи широко применяется разложение функции 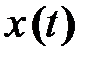в ряд Котельникова, которое позволяет существенно упростить определение коэффициентов .

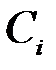Согласно теореме Котельникова произвольная функция 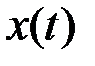с ограниченным спектром, может быть тождественно представлена счетным множеством ее значений, взятых через интервал времени 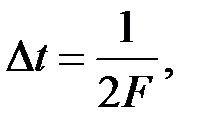где F - верхняя граничная частота спектра сигнала. В этом случае функции

,

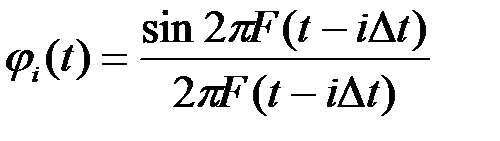образующие систему ортогональных функций, отличаются друг от друга только сдвигом по оси времени t на величину кратную 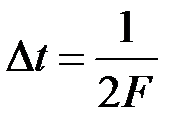, при этом каждая из них достигает своего максимального значения в те моменты времени, когда значения всех остальных функций равны нулю. Коэффициенты разложения определяются по формуле

,

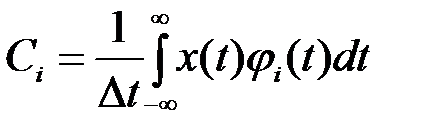которую в результате тождественных преобразований можно привести к виду: 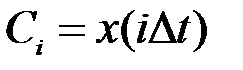, то есть коэффициент 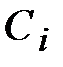равен значению функции 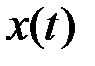в момент, когда функция 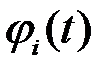достигает своего максимального значения.

Если дискретизации подлежит нормальный (гауссов) случайный процесс, энергетический спектр которого имеет прямоугольную форму, то коэффициенты 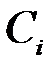будут статистически независимыми случайными величинами, которые совпадают со значениями случайной функции 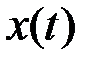, взятыми с шагом Dt [9].

Таким образом, непрерывные сообщения можно передавать в цифровом виде, то есть в виде последовательности чисел, при этом каждое число приближенно выражает величину соответствующего коэффициента 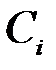.