Линейные корректирующие коды

Надежность передачи сообщений по каналу связи при наличии помех зависит от вида выбранного кода. Под кодом будем понимать множество разрешенных (передаваемых) кодовых слов, которые выбираются из множества входных канальных последовательностей (кодовых слов). Разрешенные кодовые слова (код) следует выбрать таким образом, чтобы вероятность ошибки была минимальной. Вероятность ошибки в данном случае является критерием, т.е. количественной характеристикой качества функционирования системы связи. Она показывает, как часто ошибается приемник (код) в заданной помеховой обстановке и позволяет выбрать наилучший. Приемник (код), обеспечивающий минимум вероятности ошибки, называется оптимальным в заданной помеховой обстановке. Этот критерий был предложен академиком Котельниковым, а соответствующий оптимальный приемник был назван им «идеальным наблюдателем».

С целью уменьшения вероятности ошибки, разрешенные кодовые слова следует выбирать так, чтобы они как можно меньше были похожи друг на друга, что повышает надежность их различения на фоне помех.

В качестве меры различия кодовых слов выбирается расстояние Хемминга, т.е. количество разрядов, в которых кодовые слова различаются. Поэтому корректирующую способность кода можно характеризовать минимальным расстоянием d между разрешенными кодовыми словами, которое называется минимальным кодовым расстоянием.

Декодирование осуществляется по минимуму расстояния Хемминга между принятым кодовым словом и разрешенными кодовыми словами, которые хранятся в памяти приёмника, т.е. решение принимается в пользу разрешенного кодового слова, наиближайшего к принятому. В этом случае ошибки кратности

t ≤ d – 1 обнаружимы, а кратности t < 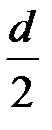или 2t + 1 ≤ d исправимы. Кратность ошибки – это количество единиц в векторе .

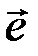При большой длине кодовых слов такой способ декодирования не удается реализовать в реальном масштабе времени из-за большого объема вычислений и, кроме этого, требуется большой объем памяти для хранения кодовых слов.

Преодолеть указанные трудности, в частности, позволяет использование линейных корректирующих кодов. В этом случае вместо запоминания всех разрешенных кодовых слов запоминается только система линейных уравнений, решениями которой являются разрешенные кодовые слова.

Основной задачей построения линейных корректирующих кодов является выбор системы линейных уравнений, которая записывается в виде:

………………………………

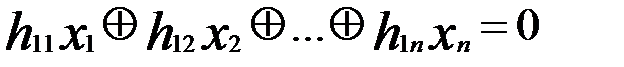
или в матричном виде H 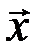= 0, где 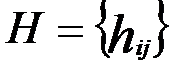- проверочная матрица, а кодовое слово размера n – 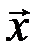= (x₁, … , x_n ). Элементы матрицы и кодового слова принимают значения только 0 или 1, при этом суммирование производится по модулю два ( ). В этой системе уравнений количество строк m выбирается меньше количества столбцов для того, чтобы система уравнений имела не единственное решение, каждое из которых является разрешенным кодовым словом. Каждое из уравнений уменьшает количество независимых переменных x_i на единицу. Поэтому количество независимых переменных, значения которых и место расположения можно выбирать произвольно, равно . 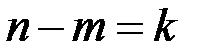Если в качестве независимых переменных выбираются первые k символов x₁,…,x_k, то код называется систематическим. Эти символы называются информационными в отличие от защитных x_k+1,…,x_n, причем защитные символы линейно выражаются через информационные. Таким образом, количество разрешенных кодовых слов равно 2^k, а общее количество входных канальных кодовых слов равно 2ⁿ.

В случае линейных корректирующих кодов сумма двух разрешенных кодовых слов является разрешенным кодовым словом. Это основное свойство, которое можно использовать в качестве определения линейного корректирующего кода, следует из равенства

,

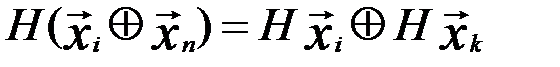где 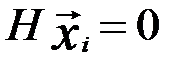и 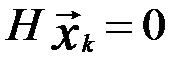по определению разрешенного кодового слова.

Рассмотрим декодирование по синдрому, использующее согласно выбранной модели канала связи принятое кодовое слово 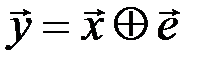, где 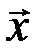- разрешенное кодовое слово, 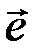- вектор ошибок.

Если 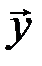совпадает с разрешенным кодовым словом ( 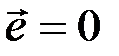или 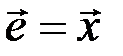- случай необнаружимой ошибки), то правая часть системы уравнений равна нулю: 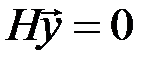, , 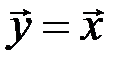и отлична от нуля, когда 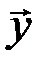- запрещенное кодовое слово: 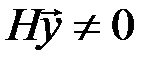. В общем случае 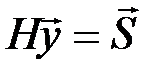, где вектор-столбец 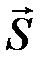называется синдромом.

Поскольку система уравнений линейна (Н – линейный оператор), то справедливы следующие преобразования:

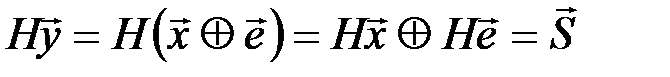
отсюда 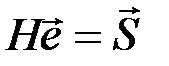, т.к. 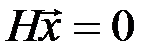по определению разрешенного кодового слова .

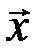Равенство 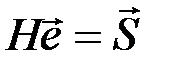устанавливает связь между синдромом 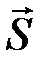и вектором ошибок 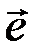, но, к сожалению, неоднозначную, поскольку не существует матрицы, обратной к Н.

Каждому значению синдрома, количество которых равно 2^m, априори до приема кодового слова 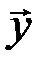, соответствует некоторое подмножество векторов 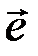, из которого при декодировании выбирается наиболее вероятный вектор 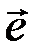с минимальным весом. (Одно из значений синдрома равно нулю, когда вектор 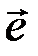совпадает с разрешенным кодовым словом, что соответствует случаю необна-ружимой ошибки).

Решение принимается в пользу кодового слова 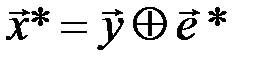, которое является разрешенным.

Таким образом, при декодировании по принятому вектору 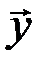вычисляется синдром, который используется при вычислени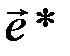и и .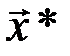

Декодирование по минимуму расстояния, по синдрому и по максимуму апостериорной вероятности 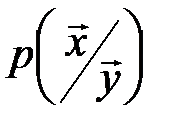эквивалентны.

Эквивалентность декодирования по минимуму расстояния и по синдрому следует из равенства 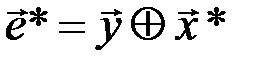, которое показывает, что расстояние между 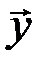и 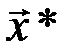измеряется весом (количеством единиц) вектора .

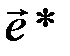Вектор 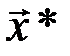является оценкой максимального правдоподобия, поскольку вектор ошибок с минимальным весом 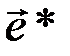, однозначно определяющий 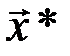, имеет максимальную вероятность при малых вероятностях ошибок в отдельном разряде вектора 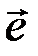( ~10^-2 – 10^-3 ).

Рассмотрим некоторые свойства линейных кодов. Количество векторов 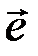в каждом из подмножеств, соответствующих различным значениям синдрома, равно количеству разрешенных кодовых слов 2^k. Для любых двух векторов 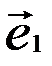и 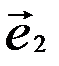, принадлежащих одному и тому же подмножеству, справедливы равенства 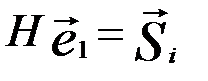и 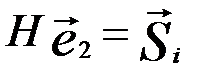. Складывая эти равенства и преобразуя суммы с учетом линейности системы уравнений (линейности оператора H) получим

,

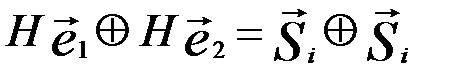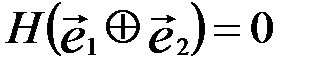
Отсюда следует, что сумма 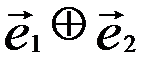является разрешенным кодовым словом по его определению, т.е. все векторы подмножества различаются между собой только на разрешенные кодовые слова.

Таким образом, если один из векторов подмножества выбрать в качестве исходного (порождающего), то все остальные можно получить в результате его сложения последовательно с каждым разрешенным кодовым словом, количество которых равно 2^k.

Минимальное кодовое расстояние в случае линейных кодов совпадает с минимальным весом разрешенных кодовых слов.

Действительно, расстояние между двумя кодовыми словами измеряется весом их суммы. Для линейного кода эта сумма совпадает с одним из разрешенных кодовых слов, вес которого определяет расстояние между двумя выбранными разрешенными кодовыми словами.

Рассмотрим свойства матрицы H, которые гарантируют заданное значение минимального кодового расстояния. Для каждого кодового слова уравнение 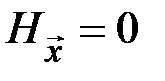означает, что сумма некоторого подмножества столбцов матрицы Н равна 0. Приумножении матрицы Н на вектор-столбец 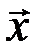из матрицы выбираются столбцы, которым соответствуют единицы в векторе 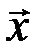. Поскольку минимальное кодовое расстояние равно минимальному весу кодовых слов, то должно существовать, по крайней мере, одно подмножество, состоящее из d столбцов матрицы H, сумма которых равна 0. С другой стороны, не может существовать ни одного подмножества из d-1 или менее столбцов, сумма которых равна 0. Если рассматривать столбцы матрицы Н как векторы, то можно сказать, что для кода с кодовым расстоянием, равным d, все подмножества из d-1 столбцов должны быть линейно независимыми. Это утверждение составляет одну из фундаментальных теорем о групповых кодах. Оно позволяет находить кодовое расстояние d группового кода, заданного матрицей Н, а также строить матрицы Н, гарантирующие заданное минимальное кодовое расстояние.

Декодированию по синдрому можно дать следующую физическую интерпретацию: вектор 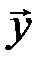подается на вход линейного дискретного фильтра, который описывается линейным оператором H, а на выходе фильтра наблюдается вектор 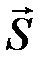. Фильтр не пропускает на выход разрешенные кодовые слова 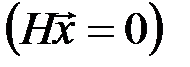, а помеха 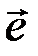, искаженная фильтром наблюдается на его выходе в виде синдрома .

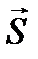По синдрому с некоторой точностью восстанавливается (оценивается) вид вектора ошибок на входе фильтра. Оценка 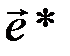этого вектора используется для компенсации вектора ошибок 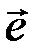, действующего в канале. Механизм компенсации можно пояснить с помощью равенства:

.

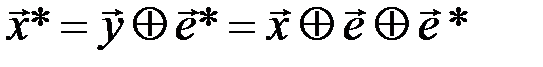При декодировании ошибка отсутствует, когда 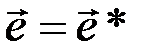.