Движение по grad для факторного эксперимента.

Для нормирования модели, получив уравнение регрессии, мы можем связать значения коэффициентов bj с компонентами вектора grad параметра оптимизации

Уравнение регрессии имеет вид: у=b₀+b₁x₁+b₂x₂+…+b_nx_n

Тогда в каждом компоненте вектора grad ставится в соответствии коэффициент уравнения регрессии

Тогда для мы получим следующее

9.5. Выбор значения

1) Необходимо подставить значение в модели вида у=f( ) b и затем дифференцирую по определить его значение, когда достигнет max значение

= const ( определяет величину шага в факторном пр-ве при движении по grad)

определяем на основании оценок коэффициента уравнения регрессии, который имеет статистический смысл, поэтому определение таким способом допустимо если выполняется условие:

2) он основан на соответствии среднеквадратичного отклонения оценок модели и величиной шага

- дисперсия коэффициентов в уравнении регрессии

n – число значимых факторов

j- номер шага

При этом способе выбора величина шага в направлении. grad параметра оптимизации зависит от номера шага, по мере приближения к экстремуму шаг уменьшается.

Но однако необходимо учитывать и абсолютную величину шага, так как иногда при большой величине получается слишком большая величина шага, при которой можно выйти за область определения фактора.

9.6. Расчет начальных значений факторов для планирования следующего этапа эксперимента.

Из первого этапа эксперимента известны коэффициенты факторных моделей b0,b1…bk, так же мы нашли дисперсию коэффициентов.

Для расчета начальных значений фактора на следующем этапе необходимо рассчитать величину шага тем или иным способом, и рассчитать - изменение факторов, которые обеспечивают движение по grad, то есть в направление max изменения функции отклика y.

Полученная точка может служить центром нового факторного эксперимента, целью которого является построение модели в новой области факторного пространства нахождения нового значения grad, последующего движения в этом направлении и т.д. до тех пор, пока не будет достигнут экстремум.

На основании первичной информации построим план.

Рототабельность плана обеспечивается проведением параллельных опытов в центре плана, а не в любой точке.

Рототабельность – зависимость дисперсии от координат.

y

x

Критерий остановки

Движение по grad целесообразно пока приращение параметра оптимизации 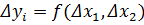достигает max.

Но так как всегда имеются случайные ошибки Δy=Δy᷈+δy

Всякое движение по grad становится бессмысленным при отрицательном grad, то есть должно выполняться условие, что Δy>0.

Проверка этой гипотезы сводится к проверке выполнения неравенства

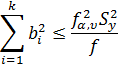
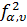- Коэффициент Стьюдента

bi- коэффициент уравнения регрессии

f=N-k-1

Если это условие выполняется, то движение по grad становится не эффективно, следовательно, данное неравенство может служить критерием остановки при движении по grad.

Глава10. План 2-го порядка

Общие понятия

Планы 2-го порядка предполагают уравнение регрессии вида

y=b₀+b₁x₁+b₂x₂+…+b_kx_k+b₁₁x₁²+b₂₂x₂²+b_kkx_k²+b₁₂x₁x₂+b₁₃x₁x₃+…+b_k-1,kx_k-1x_k

Уравнение для двухфакторной модели:

y=b₀+b₁x₁+b₂x₂+b₁₁x₁²+b₂₂x₂²+b₁₂x₁x₂

Общее число уравнение и число неизвестных коэффициентов модели =n+1=6.

Оценки коэффициентов модели содержат функции независимых факторов типа с x_i².

Этот фактор должен принимать, по крайней мере, три различных значения, то есть мы должны использовать так называемые трехуровневые факторные планы вида 3^k.

Подсчитаем число опытов для различного числа опытов:

k N

1 9

2 27

3 81

4 243

5 729

6 2187

7 6561

Уменьшить количество опытов по сравнению с трехуровневым планированием можно путем построения центральных композиционных планов второго порядка.

Для квадратичной модели композиционный план может быть получен путем добавления некоторого количества специальных точек к ядру плана, в качестве которого используются ПФП для линейной модели.

Таким образом, если к ядру плана вида ПФЭ 2^k добавить одну точку в центре плана и добавить 2k так называемых «звездных» точек, то получим центр композиционный план Бокса. Координаты звездных точек представляют собой (±α,0,0,0,0…) (0,±α,0,0)

(0,0,±α,0…) (0,0…±α).

Общее число точек центра композиционного плана Бокса:N=2^k+2k=1≤3k.

Построим матрица планирование для трехфакторного эксперимента.

N	X1	X2	X3
	+	+	+
	-	+	+
	+	-	+
	-	-	+
	+	+	-
	-	+	-
	+	-	-
	-	-	-
	+α
	-α
		+α
		-α
			+α
			-α

Ядро плана ПФП 2^k

Звездные точки 2k α-плечо звездной точки

Центр плана

10.2 Ортогональные центральные композиционные планы

При построении ортогональных композиционных планов величина α выбирается таким образом, чтобы обеспечить ортогональность плана, т.е. диагонализировать матрицу X^ТX.

Для выполнения этого условия уравнение модели необходимо преобразовать к виду.

y=a₀+b₁x₁+b₂x₂+…+b_кx_к+…+b₁₁(x₁²-β)+b₂₂(x₂²-β)+…

...+b_кк(x_к²- β)…+b₁₂x₁x₂+…+b_к-1x_к-1x_к,

В этом уравнении величина β рассчитывается из условия

β= 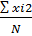или β=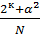

где N общее число точек плана,

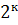-число точек в ядре плана,

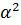- размах или плечо звездной точки композиционного плана.

Переход к уравнению регрессии от преобразованного уравнения производится с помощью формулы.

b₀=a₀-β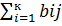

в этом случае получится

y=b₀+b₁x₁+b₂x₂+…+b₁₁x₁²+b₂₂x₂²+…

необходимо учесть следующее, для ортогональных центральных композиционных планов также как и для факторных планов Iго порядка обеспечивается независимость вычисления всех коэффициентов в уравнении регрессии, кроме b₀.

Оценку значения коэффициента b₀ необходимо пересчитать после отбрасывания незначимых квадратичных коэффициентов.

Несколько осложняется расчет дисперсии для различных коэффициентов, поскольку разные коэффициенты b₀,b_i,b_ii,b_ij, рассчитывается с различными степенями свободы. Поэтому для каждого композиционного плана пользуясь справочными данными матрицы дисперсий ковариации.

Для ортогонального плана необходимо, чтобы парные взаимодействия не были смешаны с линейными эффектами. Поэтому в качестве ядра плана при к 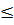4, используется только ПФЭ2^к , при к 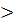4 допускается использование ДФП2^к-р.

	j	x0	x1	x2	xк	x12-β	x22-β	x122-β	x1x2	xк-1xк
Ядро плана			-1	-1	-1	1-β	1-β	1-β
			-1	-1	1-β	1-β	1-β	-1	-1
		-1		-1	1-β	1-β	1-β	-1
…		…	…	…	…	…	…	…	…
2к-р					1-β	1-β	1-β
Звездные точки	2к-р +1		+α			α2-β	-β	-β
		-α			α2-β	-β	-β
	…	…	…	…	…	…	…	…	…
			+α		-β	α2-β	-β
			-α		-β	α2-β	-β
				+α	-β	-β	α2-β
2к-р +2к				-α	-β	-β	α2-β
Центр плана	2к-р +2к+1

10.3 Выбор плеча ортогонального плана α.

Скалярное произведение любых столбцов матрицы планирования равно нулю, для любых α за исключением столбцов при квадратичных эффектах. Их скалярное произведение в общем случае не равно нулю, но является функцией α.

Приравнивая к нулю сумму скалярных произведений элементов двух столбцов с квадратичными эффектами, получим условия для выбора значений α при которых обеспечивается ортогональность плана .

α^к-р (1- )- ( - )+(2к-3)( )=0

α= .

10.4 Параметры для ортогонального центрального плана

для различных к.

Размер плана	Ядро плана	N	α	β	Элементы матрицы
С0	С1	С2	С3
	22			0,6677	0,1111	0,1667	0,5	0,2
	23		1,215	0,73	0,0667	0,0913	0,2298	0,125
	24		1,414	0,8	0,04	0,05	0,125	0,0625
	25-1		1,547	0,77	0,037	0,0481	0,0871	0,0625
	26-1		1,722	0,843	0,0222	0,0264	0,0564	0,03125
	27-1		1,885	0,9	0,0127	0,0141	0,0399	0,0156
	28-1		2,001	0,8889	0,0123	0,0139	0,0312	0,0156

С₀= С₁= .