Тема 5. Исследование двоичных полных и неполных сумматоров

Цель работы:Приобретение практических навыков синтеза суммирования двоичных и десятичных чисел

Теория и примеры выполнения задания.

Сумматоры. Комбинационные и накапливающие сумматоры двоичных чисел. Сложение в двоичной системе счисления является самой важной арифметической операцией, так как оно лежит в основе других арифметических операций: вычитания, умножения, деления.

Сумматоры предназначены для выполнения арифметических и логических операций над числами, представленными в двоичном, двоично-десятичном, троичном и др. кодах.

Для суммирования могут применяться одно- или многоразрядные сумматоры, а само суммирование осуществляется либо последовательно, начиная с младшего разряда, либо параллельно (т.е. суммируются все разряды чисел одновременно), либо параллельно-последовательно (когда многоразрядное число разбивается на группы и суммирование разрядов в группах осуществляется параллельно, а группы суммируются последовательно).

В цифровых устройствах применяются одноразрядные сумматоры на два и на три входа, причем первый называется полусумматором(ПС), а второй – полным одноразрядным сумматором (ПОС). Обе схемы реализуются на комбинационных ЛС и называются комбинационными.

Таблица состояний полусумматора (табл.5.1)

Таблица 5.1. Таблица истинности двоичного полусумматора

Вход	Выход
a	b	S	P

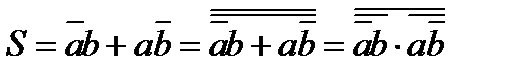(4.5)

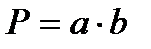
где: S – функция суммы,

P – функция переноса в старший разряд

Таблица 5.2 состояний полного сумматора

Значения переменных на входе	состояние выхода
a	b	с	S	P

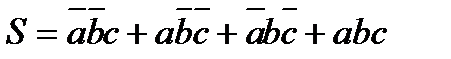(5.1)

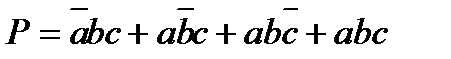
Преобразуем (1) в базисе И-НЕ:

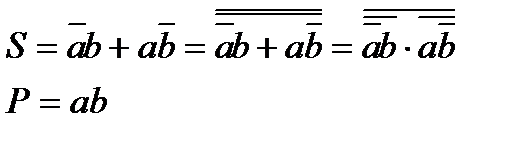(5.2)

Неполный сумматор имеет только два входа и два выхода. Один выход дает результат сложения двух бит, а второй – результат переноса, возникающий при сложении, т.е. неполный сумматор представляет собой, в принципе, элемент ИСКЛЮЧАЮЩЕЕ ИЛИ, дополненный выходом переноса.

Рисунок 5.1– Неполный сумматор (сумматор по модулю 2)

Полный же одноразрядный сумматор (ПОС), представленный таблицей истинности, имеет три входа и два выхода. На третий вход подается результат переноса предыдущего сумматора. ПОС можно построить из двух неполных (рис. 5.2).

Рисунок 5.2 – Полный сумматор на 3 входа

Карты Карно-Вейча для функции суммы S и функции переноса P, заполненные в соответствии с табл.5.2, имеют вид:

ab

c
				S 1
			6 p1iUQmlWo+xByEFGUFIFR8wUYY7SQJgf83S+ul5d55N8erma5GlVTe7Wy3xyuc6uZtW7armssp8B cpYXrWCMq4D6SN4s/ztyjGM00O5E3xfZufMirOP3ugjJSxix4JjV8R+zi5wINBjotNHsGSlh9TCN +Hqg0Gr7nZIeJ7Gk7tsOLKdEflBIq3mW52F0o5LPrqao2HPL5twCqsZQJfWUDOLSD+O+M1ZsW7wp i+1W+g6p2IjIkUDTAdVIYJy2mMH4MoRxPtej1+/3a/ELAAD//wMAUEsDBBQABgAIAAAAIQABXGQd 3QAAAAcBAAAPAAAAZHJzL2Rvd25yZXYueG1sTI/BTsMwEETvSPyDtUjcWjutWtKQTYWQQOLAoYUP cOJtEhKvo9htQ78e90SPoxnNvMm3k+3FiUbfOkZI5goEceVMyzXC99fbLAXhg2aje8eE8EsetsX9 Xa4z4868o9M+1CKWsM80QhPCkEnpq4as9nM3EEfv4EarQ5RjLc2oz7Hc9nKh1Fpa3XJcaPRArw1V 3f5oES4/u89D6T+6942qVl2yWVSri0V8fJhenkEEmsJ/GK74ER2KyFS6IxsveoR0Ga8EhNkTiKud rKMuEZYqBVnk8pa/+AMAAP//AwBQSwECLQAUAAYACAAAACEAtoM4kv4AAADhAQAAEwAAAAAAAAAA AAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnhtbFBLAQItABQABgAIAAAAIQA4/SH/1gAAAJQBAAAL AAAAAAAAAAAAAAAAAC8BAABfcmVscy8ucmVsc1BLAQItABQABgAIAAAAIQBwrUVcegIAAAcFAAAO AAAAAAAAAAAAAAAAAC4CAABkcnMvZTJvRG9jLnhtbFBLAQItABQABgAIAAAAIQABXGQd3QAAAAcB AAAPAAAAAAAAAAAAAAAAANQEAABkcnMvZG93bnJldi54bWxQSwUGAAAAAAQABADzAAAA3gUAAAAA " filled="f"> 1

ab

c
				P 0

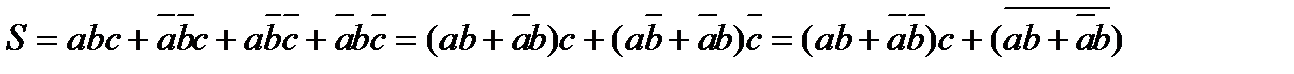(5.3)

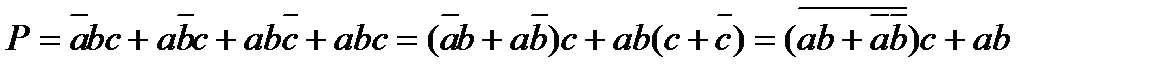
P=ab+bc+ac

Карта Карно для S показывает, что логическая функция не минимизируется, поэтому ее преобразования можно делать только с учетом удовлетворения требований минимальных аппаратных затрат, необходимых для одновременной реализации S и Р. Вариантов таких преобразований много. Один из них, реализующий (2) в базисе И-ИЛИ-НЕ имеет вид (рис.5.3):

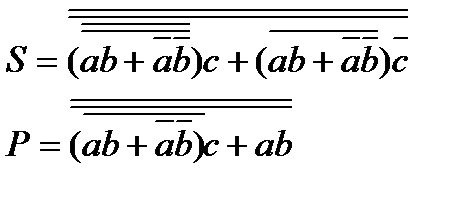(5.4)

Рисунок 5.3 – Полный сумматор на 3 входа на элементах И-ИЛИ-НЕ

S

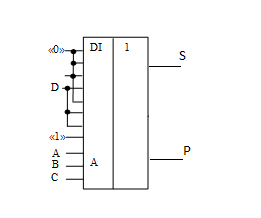
Рисунок 5.4 – Полный одноразрядный комбинационый сумматор на сдвоенном мультиплексоре.

ПОС вырабатывает выходные сигналы суммы и переноса, определяемые комбинацией цифр слагаемых, одновременно поданных на входы. Сумматор не обладает памятью и после снятия сигналов с входов сигналы S и P на выходе также снимаются. Такие сумматоры называются комбинационными.

Параллельный (многоразрядный) сумматор может быть составлен из одноразрядных, число которых равно числу слагаемых , путем соединения выхода, на котором формируется сигнал переноса данного разряда, с входом для сигнала переноса соседнего старшего разряда (рис. 5.5).

Рисунок 5.5– Сумматор параллельного типа

Последовательный сумматор можно реализовать в соответствии со схемой, приведенной на рис. 5.6.

Рисунок 5.6 – Последовательный сумматор

В сумматоре рис. 5.6 операнды А и В соответственно с регистров РгА и РгВ последовательно, начиная с младших разрядов, подаются на входы А и В сумматора. Значение суммы выводится на выход Sсумматора, а значение переноса – на выход сумматора Р, к которому подключен триггер переноса. Выход триггера соединен со входом С сумматора. После суммирования значений двух одноименных разрядов суммы и переноса производится сдвиг содержимого регистров А, В и S и образуется новое значение суммы. Количество циклов сдвига определяется разрядностью слагаемых.

К достоинству схемы относится то, что для получения эначения суммы нужен только один сумматор, но при этом время суммирования зависит от числа разрядов операндов.

Организация накапливающих сумматоров на основе комбинационных схем требует применения запоминающих регистров и может строиться, например, по схеме рис. 5.7:

Сумма

Рисунок 5.7– Сумматор накапливающего типа

Ко входам комбинационной схемы (КС) подключены два регистра слагаемых А и В, а к выходу сумматора подключен регистр суммы С, выходы которого через схемы ИЛИ могут передавать результат суммирования через регистр второго слагаемого вновь на сложение с новым значением числа А, то есть в схеме может осуществляться суммирование чисел с накоплением результатов сложения.

Рассмотренные схемы сумматоров имеют выходы S и Р. Для повышения быстродействия переносы выполняют не последовательно, а параллельно или групповым методом.

Десятичный сумматор.При сложении десятичных чисел сумматоры строят по четырехразрядному принципу.

В последние годы большинство новых ЭВМ, предназначенных для инженерных расчетов, строится так, чтобы вычисления в них выполнялись в 10 системе счисления. Это делает более удобным программирование на таких ЦВМ, обеспечивает простоту индикации промежуточных и конечных результатов, исключает блоки преобразования чисел из одной системы счисления в другую.

Задача построения десятичного одноразрядного сумматора (точнее двоично-десятичного) в принципе может решаться также, как и задача построения двоичного сумматора. Однако, если в случае двоичного сумматора требовалось реализовать 2 функции от трех двухзначных переменных (S и Р), то в случае десятичного сумматора необходимо реализовать 5 функций от 9 двухзначных переменных – по 4 переменных для каждой десятичной цифры и одна переменная – перенос из младшего разряда. При этом выходные функции будут определены лишь на 200 наборах из 2⁹=512. Можно было бы записатьСДНФ этих функций и минимизировать их известными формальными методами. Однако СДНФ в этом случае содержали бы десятки дизъюнктивных членов, что значительно затрудняет минимизацию. Кроме того, вследствие большого числа неопределенных значений функций трудно решить вопрос об их оптимальном доопределении. Поэтому при использовании двоично-десятичных кодов с весами 8421 задачу суммирования десятичных цифр решают в два этапа. На первом этапе суммируют двоичные коды десятичных цифр по правилам двоичной арифметики. На втором этапе производят коррекцию результата путем прибавления или вычитания некоторой поправки, величина которой связана с величиной нескорректированного результата. При этом могут возникать три случая.

1. Результат, полученный на 1 этапе, меньше 10. В этом случае никакой коррекции не требуется. Результат представляется четырьмя двоичными разрядами, а переноса в старший десятичный разряд нет.

2. Результат 1 этапа находится в пределах от 10 до 15. Здесь необходимо передать единичный сигнал переноса в старший десятичный разряд, а в данном десятичном из полученной суммы следует вычесть поправку, равную 10.

3. Результат 1 этапа находится в пределах от 16 до 19. В этом случае необходимо передать единицу переноса в старший десятичный разряд. Но при этом сумма в данном десятичном разряде уменьшится сразу на 16, в то время, как она должна уменьшиться только на 10. Поэтому необходимая коррекция – прибавление 6. Следует заметить, что во втором случае коррекция может быть введена точно также, как в третьем, так как вычитание цифры 10 может быть заменено сложением с ее дополнительным кодом, которым и является код цифры 6 – 0110.

На рис.5.8 ряд сумматоров реализует первый этап сложения. Наличие сигнала переноса на выходе старшего двоичного разряда означает, что результат первого этапа больше или равен 16. Кроме того, перенос в старший разряд (десятичный) должен формироваться в тех случаях , когда сумма больше или равна 10, то есть когда в ее двоичном представлении будут получены коды 1010, 1011, 1100, 1101, 1110, 1111. Для обнаружения таких кодов необходима схема из двух элементов И.

Для определения переключательной функции переноса воспользуемся картой Карно-Вейча, полученной на основе анализа выходов сумматоров S1…S4 (Таблица 5.3).

Таблица 5.3. Нахождение переключательной функции переноса

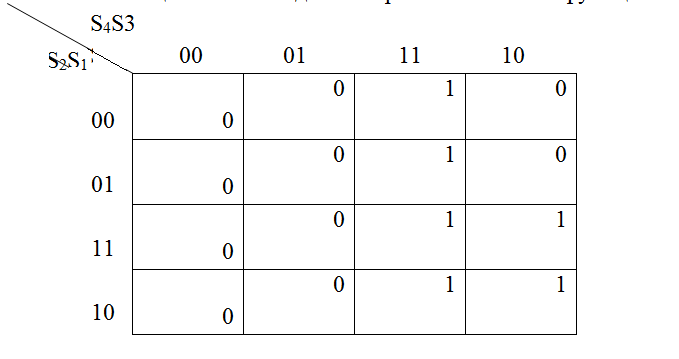
Переключательная функция формирования сигналов переноса в старшую декаду P запишется в виде:

P = S₄S₃ V S₄S_2.

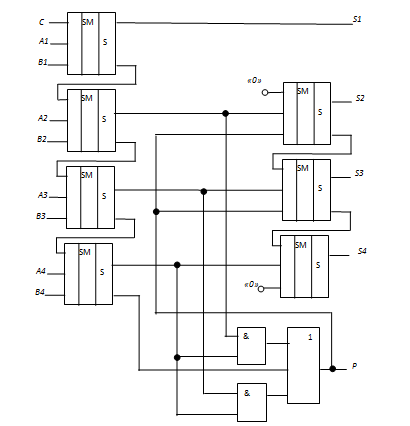
Рисунок 5.8– Схема одноразрядного десятичного сумматора

Другой ряд сумматоров предназначен для прибавления корректирующей поправки.

Схему можно упростить, заменив SM5 и SM7 полусумматорами.

По такому принципу можно строить и сумматоры, например, для кодов с избытком 3.

Буквенное обозначение в составе ИМС: сумматоры – ИМ, полусумматоры – ИЛ.

Рисунок 5.9 – Обозначение двоично-десятичного сумматора ИМ3

Задание на самостоятельную работу:

1. Выполнить синтез двоичного сумматора на 2 входа на элементах И-НЕ.

2. Выполнить синтез двоичного сумматора на 2 входа на элементах ИЛИ-НЕ.

3. Выполнить схему сумматора на элементах базиса И, ИЛИ, НЕ.

4. Выполнить схему одноразрядного двоичного сумматора на 3 входа на элементах 2-2И-ИЛИ-НЕ.

5. Выполнить синтез последовательного сумматора для суммирования двух четырехразрядных двоичных чисел.

6. Выполнить синтез параллельного сумматора для суммирования двух четырехразрядных двоичных чисел.