Тема 4. Исследование логических схем на мультиплексорах

Цель работы:Приобретение практических навыков синтеза комбинационных схем в базисе И, ИЛИ, НЕ на основе мультиплексоров

Теория и примеры выполнения задания.

Мультиплексор (коммутатор) – комбинационная многовходовая схема с одним выходом F. Входы МС подразделяются на информационные x и управляющие v. Обычно 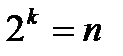, где k и n– число управляющих и информационных входов соответственно. Код, поступающий на управляющие входы, определяет один из информационных входов, значение переменной которого подается на выход F_1.

На рис.4.1. представлен MC (n=4, k=2). Этот МС построен как совокупность двухвходовых конъюнкторов (их число равно числу информационных входов), управляемых выходными сигналами

дешифратора, дешифрирующего двоичный управляющий код. Выходы конъюнктров объединены схемой ИЛИ. Данный вариант характеризуется двухступенчатой реализацией, что определяет задержку распространения сигнала, равную сумме задержки сигнала в дешифраторе и конъюнкторе.

Синтез 4-разрядного мультиплексора Рис. 4.1 выполнен в соответствии с таблицей истинности 4.1.

В интегральном исполнении применяется построение МС по линейной схем (Рис. 4.2 а,б).

В соответствии с данными уравнениями строятся реальные схемы МС, две из которых для k=2 и n=4 приведены на рис. 4.2.

Мультиплексоры широко применяются в качестве коммутаторов-селекторов сигналов для преобразования параллельного кода в последовательный, построения схем генераторов и схем сравнения кодов.

Рисунок 4.1 – Мультиплексор на 4 входа с дешифратором управления

Рисунок 4.2 – Мультиплексор на 4 входа в интегральном исполнении

Работа мультипликатора при этом описывается логическим уравнением:

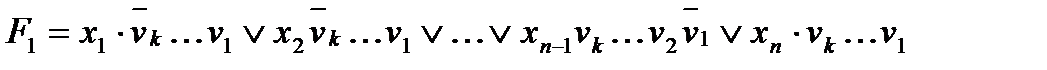(4.1)

В тех случаях, когда требуется передавать на выходы многоразрядные входные данные в параллельной форме, используется параллельное включение мультиплексоров по числу разрядов передаваемых данных. Такое объединение мультиплексоров называется мультиплексорным деревом. На рисунке 4.3 приведена функциональная схема мультиплексорного дерева, позволяющая передавать входное 16-разрядное слово на выход в последовательном коде. Так, например, чтобы выдать на выход Q мультиплесора разряд D₂ входного слова, необходимо подать на MC₁ адресный код X₁X₂= 10 и на MC₅ – X₃X₄ = 00.

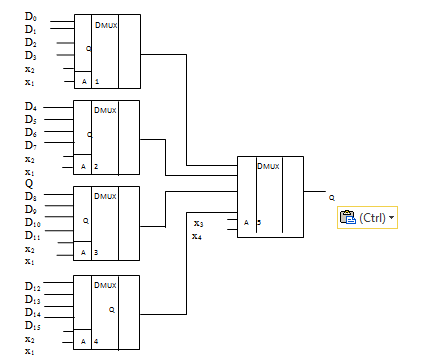
Рисунок 4.3 – Функциональная схема мультиплексного дерева

Мультиплексоры широко используются для синтеза комбинационных схем, так как применение последних позволяет значительно сократить число используемых интегральных схем.

Рассмотрим выходную функцию 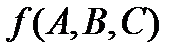формирования переноса при суммировании 3 переменных. Матрицу значений входных переменных получим непосредственным анализом карты Карно, а не путем разложения функции по минтермам с последующим преобразованием.

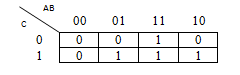
Для реализации схемы выберем мультиплексор 4x1. В качестве селекторных возьмем переменные А и В. Анализируя столбец карты, для которого АВ=00, обнаруживаем, что значение функции равно 0 для обеих клеток столбца (т.е. для обоих значений С), т.е. 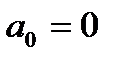. Для столбца с АВ=01 функция на выходе равна 1 при С=1, т.е. 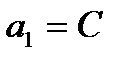. Для АВ=10, функция f также равна 1 при С=0, т.е. 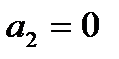. Для АВ=11 значение функции fравно 1 для обоих значений С, а 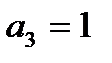. Соответствующая схема мультиплексора 4x1 приведена на рис.4.4.

Рисунок 4.4 – Мультиплексор для реализации функции переноса

Мультиплексоры с четырьмя входными линиями обычно размещают по 2 на одном кристалле. При этом селекторные линии к ним являются общими. Такое конструктивное решение является очень удобным при логическом проектировании. Восьмивходовые мультиплексоры находят широкое применение, так как компактно размещаются на одном кристалле. Их можно использовать для схем с 4-мя или большим числом входных переменных. В качестве примера рассмотрим схему компаратора, карта которого приведена на рис. 4.5. На этой карте представлены значения выходной функции f_1., причем 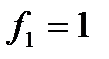в тех случаях, когда три или большее число входных переменных принимают значения 1. Если из четырех исходных переменных (А, В, С,D)три являются селекторными, то каждой входной линии мультиплексора должнысоответствовать значения в двух клетках карты Карно. Из этих пар клеток по существу получается карта Карно для оставшейся переменной D. Для ABC=000 значение функции 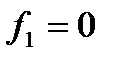как при 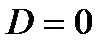, так и при 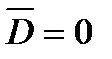. Следовательно 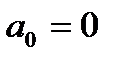. То же справедливо для ABC=001, 010 и 100, а поэтому 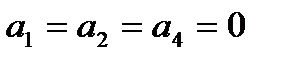. Однако для ABC=011, 101 и 110 пр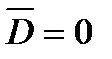и и 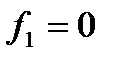, а при 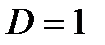, значение 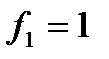; следовательно 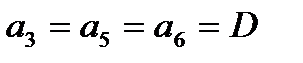. При ABC=111 значение 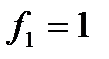как при 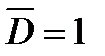, так и при 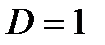, а поэтому 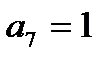. На рис. 4.5 показана реализация этой схемы на восьмивходовом мультиплексоре.

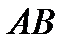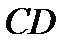Карта Карно-Вейча компаратора 3 из 4

Рисунок 4.5 – Компаратор 3 из 4

Задание на самостоятельную работу:

1. Построить мультиплекор на 4 входа, используя схемы двухвходовых мультиплексоров.

2. На базе мультиплексора на 4 входа реализовать переключательную функцию, заданную преподавателем.

3. Реализовать мультиплексное управление восемью семисегментными индикаторами.

4. На основе мультиплексора на 8 входов и 2 выхода сумматор на 3 входа.