Тема 3. Исследование дешифраторов, мультиплексоров, демультиплексоров, двоичных компараторов

Цель работы:Приобретение практических навыков синтеза комбинационных схем на произвольное число входов и выходов.

Теория и примеры выполнения задания.

Дешифраторами называются комбинационные логические схемы, преобразующие код числа, поступающий на входы, в управляющий сигнал только на одном из выходов. Если на входы дешифратора подается двоичный код числа, то функционирование двоичного дешифратора можно описать с помощью выражений:

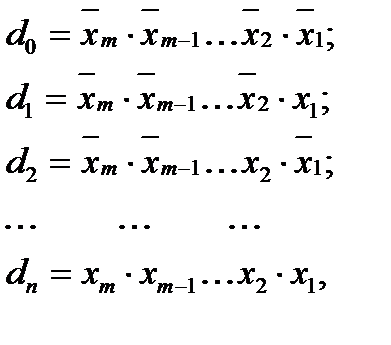(3.1)

если 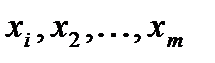- сигналы на входах дешифратора,

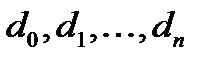- сигналы на выходах дешифратора.

Таким образом, дешифратор представляет собой не что иное, как совокупность схем совпадений, формирующих управляющий сигнал только на одном из выходов, в то время как на остальных выходах управляющий сигнал отсутствует. По этой причине дешифраторы часто называются избирательными схемами.

При дешифрации n-разрядного двоичного кода и реализации всех комбинаций этого кода число выходов дешифратора:

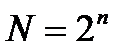
В зависимости от разрядности дешифруемого кода и функциональных возможностей ряда логических ИС, находящихся в распоряжении разработчика, дешифратор может быть выполнен на основе одноступенчатой(линейной) и многоступенчатой схем дешифрации. Среди многоступенчатых схем можно выделить прямоугольные (матричные) и пирамидальные схемы построения дешифратора.

Линейные дешифраторы выполняются прямой схемной реализацией выражений вида (3.1) без какого-либо их логического преобразования, т.е.представляют собой по существу N независимых по выходам вентилей с числом входов m у каждого.Пусть, например, m=3, N=8, тогда выражения для функции выходов дешифратора имеют вид:

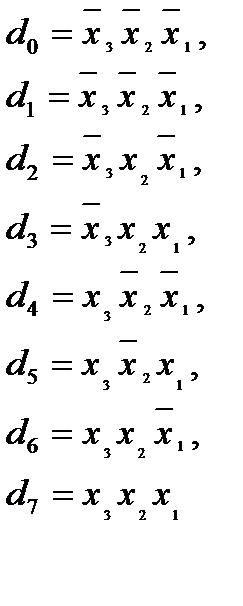Рисунок 3.1 – Дешифратор на 3 входа

Переключательные функции дешифратора рис.3.1 записаны на основе

нижеприведенной таблицы истинности (таблица 3.1)

Таблица 3.1истинности дешифратора

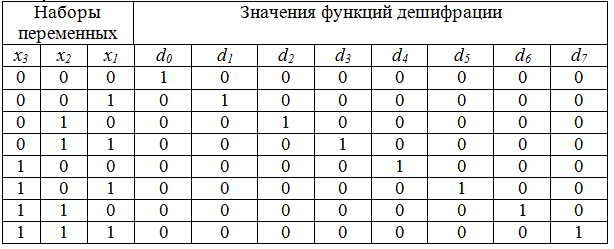
Одноступенчатые дешифраторы наиболее эффективны, когда разрядность входного кода M не превышает число входов m схемы И интегральной микросхемы. Отсюда и быстродействие линейных дешифраторов (ЛД) является максимальным по сравнению с другими схемами дешифрации и равно средней задержке типового элемента ИС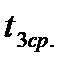

Прямоугольный дешифратор содержит первую ступень из нескольких линейных дешифраторов, на каждом из которых дешифруется группа разрядов входного слова.

В серии ИМС дешифратор маркируется буквами ИД.

Рисунок 3.2 – Прямоугольный дешифратор на 16 выходов

Демультиплексор (ДМС, DMUX) – схема, выполняющая функцию обратную функции мультиплексора, т.е. это комбинационная схема, имеющая одининформационный вход (x₁), n информационных выходов (F₁-Fn) и k управляющих входов 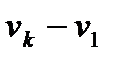. Обычно, так же как и для мультиплексора, .

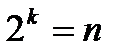Работа ДМС описывается логическими уравнениями:

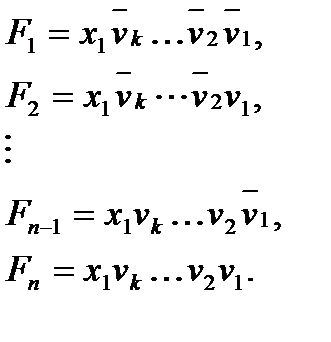(3.2)

Схема ДМС (n=4, k=2), построенная по данным уравнениям приведена на рис. 4.26 (a, b) а ее функциональное обозначение – на рис.4.26c.

Демультиплексорное дерево, представляющее собой демультиплексор на 16 выходов, приведено на рис. 3.4d.

ДМС эффективно используются для преобразования последовательного кода в параллельный. Совместное использование МС с ДМС (рис. 3.5) обеспечивает последовательную передачу информации с преобразованием параллельного кода в последовательный и последовательного в параллельный. В таком применении в качестве управляющих сигналов используются выходы двоичного счетчика.

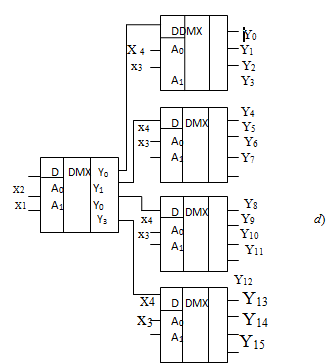
Рисунок 3.5 – Структура включения МС и ДМС для передачи информации

В серии интегральных схем демультиплексоры имеют обозначения:ИД, КП.

Схемы сравнения слов с константами. Пусть А=а₁…a_n – n-разрядное слово и K=k₁…k_n – константы. Функциональная схема вычисляющей значение x_l логического условия А=К синтезируется следующим образом. Константа К определяет единственный двоичный набор, на котором функция x_l=j_l(a₁, …,a_n) должна принимать значение 1. Поэтому функция j_lдолжна представляться конституентой 1.

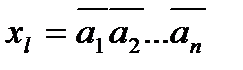, где

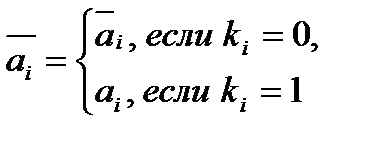(3.3)

Например, логическим условиям: х₁:=(А=0); х₂:=(А=1010); х₃:=(А=1111), где А=а₁а₂…а₄, соответствуют следующие булевы функции 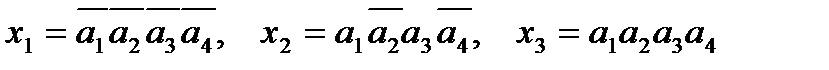, на основе которых построена схема на рисунке 3.6, формирующая, в частности, значения осведомительных сигналов х₁, х₂, х₃. В этой схеме слово А снимается с выходов четырехразрядного регистра А.

Рисунок 3.6 – Схема сравнения с константой

Логическому условию А¹К соответствует булева функция, принимающая значение x_l =0 на двоичном наборе K=k₁k₂…k_n и значении x_l =1 на всех остальных наборах. Такая функция должна содержать единственную конституенту нуля, соответствующую набору К.

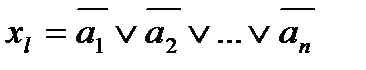
где

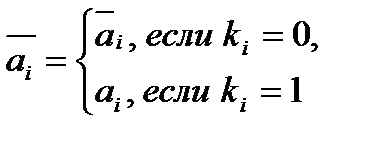(3.4)

Например, логическим условиям х₄:=(А¹0) и х₅:=(А¹1010) соответствует следующая булева функция:

(3.5)

Логическому условию А<К, принимающему значения x_l =1, если А<К, и значение x_l =0, если А³К соответствует булева функция j_l(a₁, …,a_n), принимающая значение 1 на каждом из наборов 0, 1,…,К и значение 0 на всех остальных наборах К, К+1,…,2ⁿ-1. Эту функцию можно представить дизъюнкцией конституент 1, соответствующей наборам 0, 1, …, К-1.

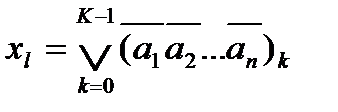, (3.6)

где буква 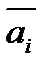определяется формулой (3.6).

Например, логическому условию х₄:=(А<1010), где А=а₁а₂…а₄, соответствует булева функция, представленная на рисунке в виде карты Карно:

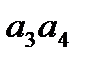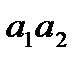Минимальная форма этой функции 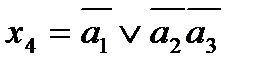. Аналогичным образом синтезируются схемы, вычисляющие логические условия вида А≤К, А>К, А³К.

Схемы сравнения на равенство. Логическое условие А=В, где А=а₁а₂…а₄, В=b₁b₂…b₄ n-разрядные слова, вычисляются комбинационной схемой, называемой схемой сравнения (по равенству). Значения А и В равны, если одновременно равны их одноименные разряды a_i, b_i, i=1,…,n. Таблица истинности, где

r_i – признак равенства значений a_i и b_i;

q_i - признак неравенства, представлена ниже:

Таблица 3.2 истинности значений функций равенства и неравенства

ai	bi	ri	qi

r_i определяется следующей булевой функцией:

.

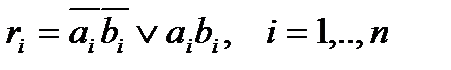Признак равенства двух n-разрядных слов вычисляется как конъюнкция

R=r_1..r₂...r_n.

По вышеизложенным выражениям построена схема сравнения трехразрядных слов А и В (Рис. 3.7):

Рисунок 3.7 – Схема сравнения двух трехразрядных слов

Если значения слов представляются в парафазном коде цена n-разрядной схемы сравнения составляет 7n единиц по Квайну. Время сравнения, определяемое промежутком от момента поступления слов А, В до момента выработки осведомительного сигнала R cоставляет t_ср=3t, где t - задержка сигнала на одном логическом элементе.

Схема, вычисляющая значения логического условия А¹К строятся аналогично. Из таблицы истинности следует, что значение признака неравенства q_iодноименных разрядов a_i, b_iслов А и В, определяется булевой функцией:

.

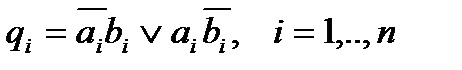Слова А и В не равны, если хотя бы в одном разряде q_i=1.

Схемы сравнения на больше-меньше.Вычисление значения логического условия A>B, где А=а₁а₂…а_n, В=b₁b₂…b_n n-разрядные слова называется сравнением слов на больше-меньше. Значение A>B можно вычислить с помощью сумматора путем определения знака разности 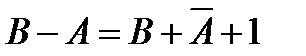, где 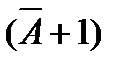- дополнительный код значения А, используемый для замены операции вычитания на сложение. В соответствии с правилами машинной арифметики разность (В-А)<0, если перенос из старшего разряда суммы 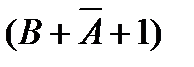отсутствует, и разность (В-А)³0, если формируется перенос из старшего разряда суммы. Следовательно, отсутствие переноса свидетельствует об истинности отношения A>B, а наличие переноса – о ложности этого отношения. Если для вычисления отношения A>B должна использоваться специальная схема (нет необходимости в использовании сумматора), то для сравнения на больше-меньше используется n-подсхем формирования переносов. Такие подсхемы П объединяются в схему сравнения на больше-меньше в соответствии с рисунком 3.8:

Рисунок 3.8 – Схема сравнения на больше-меньше

На вход схемы подается обратный код 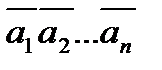слова А и прямой код b₁b₂…b_n слова В. Для получения дополнительного кода используется вход переноса в младший разряд P_n=1. Перенос из старшего разряда q_iопределяет значение отношения A>B: если q_i =0, то A>B, то есть отношение истинно, если q_i =1, то A≤B, то есть отношение ложно. Из рисунка видно, что цена одной схемы П составляет 8 единиц по Квайну и задержка сигнала переноса P_i-2t. Следовательно, цена схемы сравнения n-разрядных слов равна 8n единиц и время сравнения t_ср=2nt+t= (2n+1)t.

Задание на самостоятельную работу:

1. Каскадным включением только дешифраторов на 2 входа построить дешифратор на 16 выходов.

2. Построить преобразователь двоичного четырехразрядного кода в код с избытком 3.

3. Построить преобразователь кода 2 из 5 в двоичный код.

4. Построить преобразователь кода 2421 в код семисегменного индикатора.

5. Построить компаратор, реализующий функцию К≥9 для 4 двоичных переменных.

6. Выполнить синтез демультиплексора на 16 выходов, используя демультиплексоры на 4 выхода.