Теорема Вариньона о моменте равнодействующей

Теорема Вариньона о моменте равнодействующей

Если система сил имеет равнодействующую, то момент этой равнодействующей относительно любого центра равен алгебраической сумме моментов сил системы относительно того же центра. Доказательство: Пусть система сил F1, F2, F3 … приводится к равнодействующей, приложенной в точке O. Такая система не находится в равновесии (R ≠ 0). Уравновесим эту систему силой R’, равной равнодействующей R, направленной по линии ее действия в противоположную сторону (аксиома о двух силах).

Таким образом, система исходных сил F1, F2, F3 … и уравновешивающей силы R’ находится в равновесии и должна удовлетворять уравнениям равновесия, например:

Поскольку сила R’, равна равнодействующей R и направлена по линии ее действия в противоположную сторону, то MA(R’) = - MA(R). Подстановка этого равенства в уравнение равновесия дает:

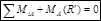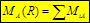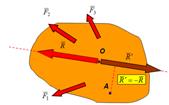
Различные формы системы условий равновесия плоской системы сил.

Первая форма условий равновесия

Для равновесия произвольной плоской системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы главный вектор R этих сил и их главный момент Mo относительно произвольной точки O, лежащей в плоскости действия этих сил, были равны нулю, т.е.

ΣFk = 0, ΣMo(Fk) = 0 (1.3)

В координатной форме эти условия выражаются следующими тремя уравнениями:

ΣFkx = 0, ΣFky = 0, ΣMo(Fk) = 0.

Вторая форма условий равновесия (теорема о трех моментах)

Теорема о трех моментах – алгебраическая сумма моментов сил относительно трех произвольных точек A,B,C, не лежащих на одной прямой, равна нулю, т.е.

ΣMA(Fk) = 0, ΣMB(Fk) = 0, ΣMC(Fk) = 0; (1.5)

Третья форма условий равновесия

Алгебраическая сумма моментов всех сил относительно двух любых точек A и B равна нулю и сумма проекций этих сил на ось Ox, не перпендикулярную к прямой, проходящей через точки A и B , равна нулю, т.е. ΣMA(Fk) = 0, ΣMB(Fk) = 0, ΣFkx = 0. (1.6)

Связи и реакции связей

Свободное тело – свобода перемещений тела не ограничивается никакими другими телами.

Несвободное тело – его движение ограничено другими телами.

Связь – тело, ограничивающее свободу перемещений объекта.

Реакция связи – сила, действующая на объект со стороны связи.

Принцип освобождаемости от связи – несвободное тело можно рассматривать как свободное, если отбросить связи и заменить их действие соответствующими реакциями.

1. Нить, шарнирный стержень: Реакция нити (стержня) направлена по нити (по стержню).

2. Абсолютно гладкая поверхность: Реакция гладкой поверхности направлена перпендикулярно общей касательной плоскости, проведенной к соприкасающимся поверхностям тела и связи.

3. Неподвижный цилиндрический шарнир: Реакция неподвижного шарнира проходит через центр шарнира перпендикулярно оси шарнира и имеет произвольное направление. Реакцию неподвижного шарнира можно разложить на две составляющие, например, Rx и Ry, параллельные координатным осям.

4. Подвижный цилиндрический шарнир: Реакция подвижного шарнира проходит через центр шарнира перпендикулярно оси шарнира и плоскости опирания.

5. Неподвижный сферический шарнир: Реакция неподвижного сферического шарнира проходит через центр шарнира и имеет произвольное направление в пространстве. Реакцию неподвижного

сферического шарнира можно разложить на три составляющие, например, Rx, Ry, Rz, параллельные координатным осям.

6. Жесткая плоская заделка: В жесткой плоской заделке возникает три реактивных усилия: две составляющие реактивные силы Rx и Ry, а также реактивный момент (пара сил) MA .

Общее правило для связей любого вида:

Если связь препятствует одному или нескольким перемещениям (максимальное число перемещений – три поступательных и три вращательных), то по направлению именно этих и только этих перемещений возникают соответствующие реакции (силы и моменты).

Аксиомы статики

А1. Аксиома инерции – Под действием взаимно уравновешенной системы сил тело находится в состоянии покоя или равномерного прямолинейного движения.

А2. Аксиома двух сил – Если тело под действием двух сил находится в равновесии, то эти силы равны по модулю и направлены по одной прямой в противоположные стороны. Такие две силы представляют собой простейшую взаимно уравновешенную систему сил.

А3. Аксиома присоединения – Если к заданной системе сил присоединить (или изъять) взаимно уравновешенную систему сил, то кинематическое состояние тела не изменится.

Следствие из аксиомы присоединения – Кинематическое состояние тела не изменится, если силу перенести по линии ее действия.

А4. Аксиома параллелограмма – Равнодействующая двух пересекающихся сил равна диагонали параллелограмма, построенного А5. Аксиома действия и противодействия – Всякому действию соответствует равное и противоположное противодействие (III закон Ньютона).

А6. Аксиома отвердевания – Равновесие деформируемого тела сохраняется при его затвердевании (обратное справедливо не всегда).

Принцип освобождаемости от связи – несвободное тело можно рассматривать как свободное, если отбросить связи и заменить их действие соответствующими реакциями.

Пара сил

Пара сил – совокупность двух параллельных друг другу сил, равных по величине и направленных в противоположные стороны. Пара сил более не может быть упрощена (не может быть заменена одной силой) и представляет собой новую силовую характеристику механического взаимодействия.

Момент пары сил на плоскости равен произведению модуля любой из сил пары на плечо пары, взятым со знаком + (плюс), если вращение плоскости под действием пары сил происходит против часовой стрелки, и со знаком – (минус) в противном случае.

Теорема. Момент пары не зависит от выбора полюса.

В этом можно убедиться вычислением суммы моментов от каждой из сил относительно любого центра, например точки А:

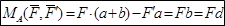
Теорема о сложении пар сил на плоскости – Систему пар сил на плоскости можно заменить одной парой, момент которой равен алгебраической сумме моментов исходных пар. Кинематическое состояние тела не изменится.

Теорема Вариньона о моменте равнодействующей

Если система сил имеет равнодействующую, то момент этой равнодействующей относительно любого центра равен алгебраической сумме моментов сил системы относительно того же центра. Доказательство: Пусть система сил F1, F2, F3 … приводится к равнодействующей, приложенной в точке O. Такая система не находится в равновесии (R ≠ 0). Уравновесим эту систему силой R’, равной равнодействующей R, направленной по линии ее действия в противоположную сторону (аксиома о двух силах).

Таким образом, система исходных сил F1, F2, F3 … и уравновешивающей силы R’ находится в равновесии и должна удовлетворять уравнениям равновесия, например:

Поскольку сила R’, равна равнодействующей R и направлена по линии ее действия в противоположную сторону, то MA(R’) = - MA(R). Подстановка этого равенства в уравнение равновесия дает:
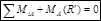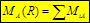