Синтез и исследование системы с модальным управлением

Цель работы– освоение методики синтеза модального регулятора и анализ возможностей модального управления.

Основные сведения

Модальным называется управление, обеспечивающее размещение корней характеристического полинома (ХП) в заданных точках комплексной плоскости. 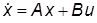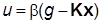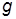В простейшем случае для исходной системы (объекта управления) с одним входом, описываемой уравнением , где x – n-мер-ный вектор состояния, а u – скалярное управление, модальный регулятор (МР), представляющий собой линейную обратную связь по состоянию, описывается уравнением , где – задающее воздействие;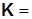 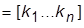– матрица обратной связи; 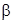– коэффициент, назначением которого можно обеспечить заданный коэффициент передачи системы от входа g к заданному выходу y. Если, например, требуется синтезировать систему, удовлетворяющую заданным требованиям к перерегулированию 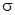и времени регулирования 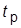, то методика синтеза МР должна включать в себя следующие этапы.

1. Составить математическое описание объекта управления и записать матрицы А и В.

2. Исследовать управляемость пары (А, В). Если матрица ( 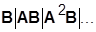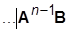) имеет полный ранг, то для данного объекта может быть синтезирован МР.

3. Записать выражения для матрицы новой системы 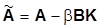и ее ХП 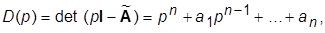коэффициенты которого представляют собой композиции параметров объекта и неизвестных коэффициентов .

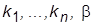4. В соответствии с заданным значением 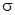по справочнику выбрать тип стандартного желаемого ХП 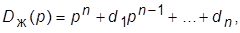где 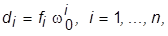и выписать значения коэффициентов 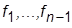( 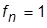) и относительного времени регулирования .

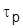5. Зная требуемое значение 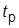, вычислить среднегеометрический корень полинома как 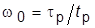, после чего вычислить коэффициенты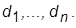

6. Выразить коэффициент передачи системы (требуемое значение которого известно) через коэффициенты 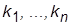и, возможно, .

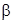7. Приравнивая коэффициенты при одинаковых степенях p желаемого и фактического полиномов ( 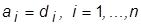), составить систему n линейных алгебраических уравнений. Дополнив ее уравнением из предыдущего пункта и решив, найти элементы 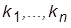матрицы 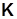и коэффициент .

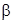Программа работы

Объектом синтеза и анализа является система регулирования скорости двигателя, соединенного с механизмом упругой кинематической связью. Исходная система и система с МР представлены одной схемой на рисунке, из которой исходная система получается при 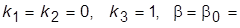= 10. На схеме 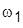и 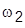– угловые скорости двигателя и механизма; 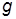– задание скорости; 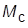– момент сопротивлений; 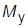– момент сил упругост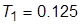и; с и 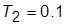с– постоянные времени двигателя и механизма; 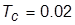си 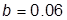– постоянная времени жесткости и коэффициент внутреннего трения; b – коэффициент, описывающий предварительный усилитель и быстродействующий внутренний контур регулирования тока.

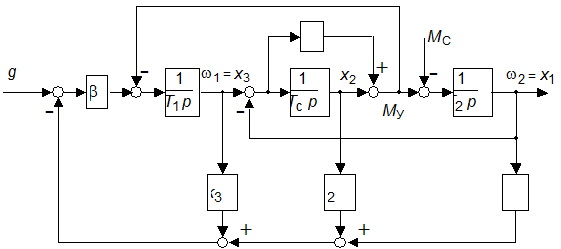
Работа состоит из двух этапов – подготовительного, выполняемого в домашних условиях, и исследовательского, выполняемого в лаборатории.

Задание для домашней подготовки: определить параметры МР 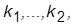b, использовав методику из 5.1, для двух типов стандартных полиномов – Баттерворта и биномиального (их описания даны в лабораторной работе № 2). Значение 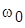взять из вариантов, приведенных ниже:

Вариант

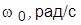При расчете регулятора учесть, что в исходной системе коэффициент передачи равен единице, а в системе с МР равен 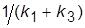, в силу чего получаем уравнение связи 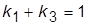. Для самопроверки: окончательные выражения для параметров МР имеют следующий вид:

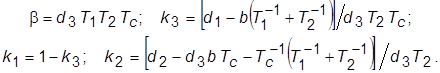
Исследовательская часть состоит из следующих этапов.

1. Выполнить анализ свойств исходной системы: получить ПХ по задающему воздействию (с копией экрана), считая выходной переменную 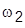, и определить 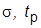и частоту колебаний; определить показатель колебательности М, полосу пропускания 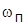и максимум 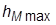ПХ по возмущению.

2. Для каждого из двух вариантов назначения ХП выполнить анализ динамических свойств системы с МР, получив ПХ по задающему и возмущающему воздействиям и определив 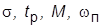. Для одной из ПХ сделать копию экрана.

Содержание отчета

1. Структурная схема исходной системы, численные значения ее параметров, ПФ исходной разомкнутой системы.

2. Полный расчет МР, включая запись матрицы системы, анализ управляемости, определение желаемого ХП и параметров МР.

3. Результаты анализа исходной системы и системы с МР, согласно программе работы, и комментарии к ним. (Учесть, что теоретические значения относительного времени регулирования для систем с ПФ без нулей, имеющих ХП Баттерворта и биномиальный, равны, соответственно, 5.9 и 6.3, а перерегулирование при баттервортовом распределении составляет 7.1%.)

Контрольные вопросы

1. Что такое модальное управление? Что представляет собой МР?

2. Какой матрицей определяются динамические свойства исходной системы? системы с МР?

3. Какую роль в синтезе МР играет свойство управляемости исходной системы и какова роль стандартных полиномов?

ПРИЛОЖЕНИЕ