Модифицированный метод Эйлера.
Для определения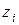 
воспользуемся обычной формулой Эйлера, а для определения 
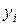будет естественным использовать уточненную формулу, т.е.
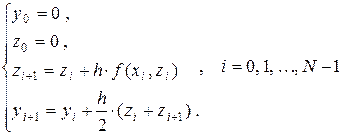(Л4.3)
Пример соответствующей M-функции (ниже задано 
, 
, 
):
function consol
s=input('s=');g=input('g=');L=input('L=');n=input('n=');
h=L/n;c=0.02*(s+g);ej=1/c;
x=0:h:L;z=zeros(size(x));y=z;
for i=1:n
z(i+1)=z(i)+h*f(x(i),z(i));
y(i+1)=y(i)+h*(z(i)+z(i+1))/2;
end
ixyz=[(0:n);x;y;z];
fprintf('\n'),fprintf('%3s %4s %6s %6s','i','x','y','z')
fprintf('\n'),fprintf('%3d %4.1f %6.4f %6.4f\n',ixyz)
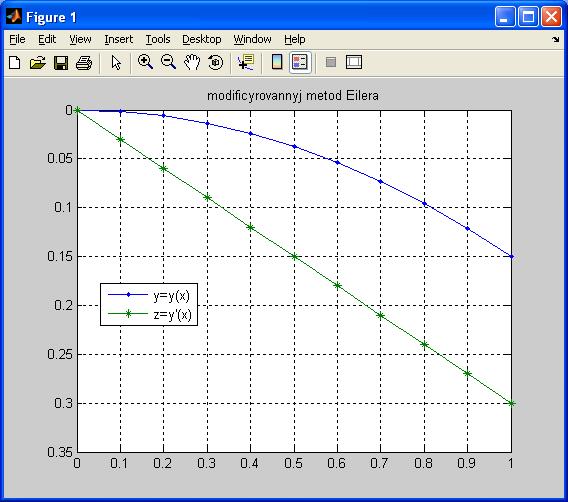
plot(x,y,'.-',x,z,'*-'),grid on
legend('y=y(x)','z=y''(x)',0),title('modificyrovannyj metod Eilera')
function dzdx=f(x,z)
dzdx=m(x)/ej*sqrt((1+z^2)^3);
end
function M=m(x)
M=1/sqrt((1+(c*x)^2)^3);
end
end
Результаты счета:
s=12
g=3
L=1
n=10
i x y z
0 0.0 0.0000 0.0000
1 0.1 0.0015 0.0300
2 0.2 0.0060 0.0600
3 0.3 0.0135 0.0900
4 0.4 0.0240 0.1200
5 0.5 0.0375 0.1500
6 0.6 0.0540 0.1800
7 0.7 0.0735 0.2100
8 0.8 0.0960 0.2400
9 0.9 0.1215 0.2700
10 1.0 0.1500 0.3000
>>
2. Использование встроенной функции ode45, предназначенной для решения задачи Коши для систем обыкновенных дифференциальных уравнений 1-го порядка вида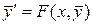 
.
В данной функции реализуются одношаговые методы Рунге-Кутта 4-го и 5-го порядков. Это классический подход, рекомендуемый для начальной пробы решения. Во многих случаях (если система уравнений не является жесткой) можно получить удовлетворительные результаты. Таким образом, данную функцию применяют довольно часто, особенно тогда, когда неизвестны характеристики задачи.
Предварительно представим систему (Л4.2) в виде
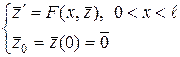, (Л4.3)
где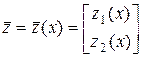 
, 
, 
,
, 
.
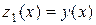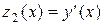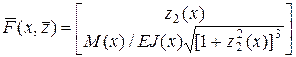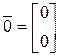При обращении к ode45 входными параметрами будут дескриптор имени функции, реализующей вычисление вектор-функции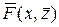 
, массив, содержащий значения левого и правого конца диапазона изменения переменной 
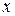, а также вектор начальных значений 
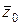. Выходными параметрами будут массивы 
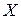и 
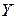, где
, 
, 
, 
.
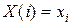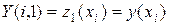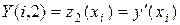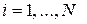Пример соответствующей M-функции (ниже задано , ):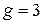
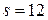function consol_ode45
s=input('s=');
g=input('g=');
c=0.02*(s+g);
EJ=1/c;
x0xL=input('[x0 xL]=');
z0=input('[z10 z20]=');
[X Z]=ode45(@F,x0xL,z0);
n=length(X);
fprintf('\n'),fprintf('%3s %6s %6s %6s','i','x','y','y'''),fprintf('\n')
for i=1:n
fprintf('%3d %6.4f %6.4f %6.4f\n',i,X(i),Z(i,:))
end
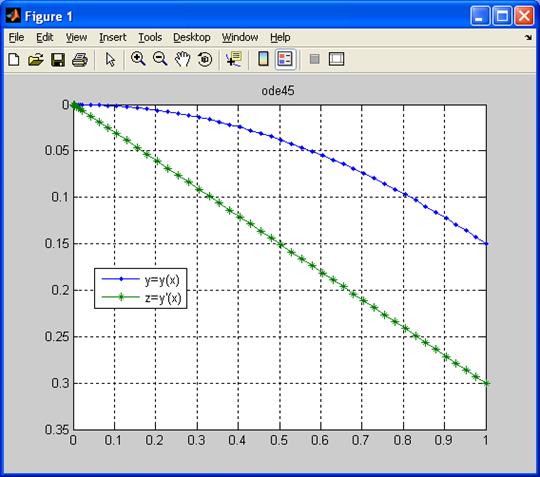
plot(X,Z(:,1),'.-',X,Z(:,2),'*-'),grid on
legend('y=y(x)','z=y''(x)',0),title('ode45')
function dz=F(x,z)
dz=zeros(2,1);
dz(1)=z(2);
dz(2)=M(x)/EJ*sqrt((1+z(2)^2)^3);
end
function m=M(x)
m=1/sqrt((1+(c*x)^2)^3);
end
end
Результаты счета:
s=12
g=3
[x0 xL]=[0 1]
[y0 z0]=[0 0]
i x y y'
1 0.0000 0.0000 0.0000
2 0.0002 0.0000 0.0001
3 0.0003 0.0000 0.0001
4 0.0005 0.0000 0.0002
5 0.0007 0.0000 0.0002
6 0.0015 0.0000 0.0005
7 0.0023 0.0000 0.0007
8 0.0032 0.0000 0.0010
9 0.0040 0.0000 0.0012
10 0.0082 0.0000 0.0025
11 0.0124 0.0000 0.0037
12 0.0166 0.0000 0.0050
13 0.0208 0.0001 0.0062
14 0.0417 0.0003 0.0125
15 0.0626 0.0006 0.0188
16 0.0836 0.0010 0.0251
17 0.1045 0.0016 0.0313
18 0.1295 0.0025 0.0388
19 0.1545 0.0036 0.0463
20 0.1795 0.0048 0.0538
21 0.2045 0.0063 0.0613
22 0.2295 0.0079 0.0688
23 0.2545 0.0097 0.0763
24 0.2795 0.0117 0.0838
25 0.3045 0.0139 0.0913
26 0.3295 0.0163 0.0988
27 0.3545 0.0188 0.1063
28 0.3795 0.0216 0.1138
29 0.4045 0.0245 0.1213
30 0.4295 0.0277 0.1288
31 0.4545 0.0310 0.1363
32 0.4795 0.0345 0.1438
33 0.5045 0.0382 0.1513
34 0.5295 0.0421 0.1588
35 0.5545 0.0461 0.1663
36 0.5795 0.0504 0.1738
37 0.6045 0.0548 0.1813
38 0.6295 0.0594 0.1888
39 0.6545 0.0643 0.1963
40 0.6795 0.0693 0.2038
41 0.7045 0.0744 0.2113
42 0.7295 0.0798 0.2188
43 0.7545 0.0854 0.2263
44 0.7795 0.0911 0.2338
45 0.8045 0.0971 0.2413
46 0.8295 0.1032 0.2488
47 0.8545 0.1095 0.2563
48 0.8795 0.1160 0.2638
49 0.9045 0.1227 0.2713
50 0.9284 0.1293 0.2785
51 0.9522 0.1360 0.2857
52 0.9761 0.1429 0.2928
53 1.0000 0.1500 0.3000
>>
>> 
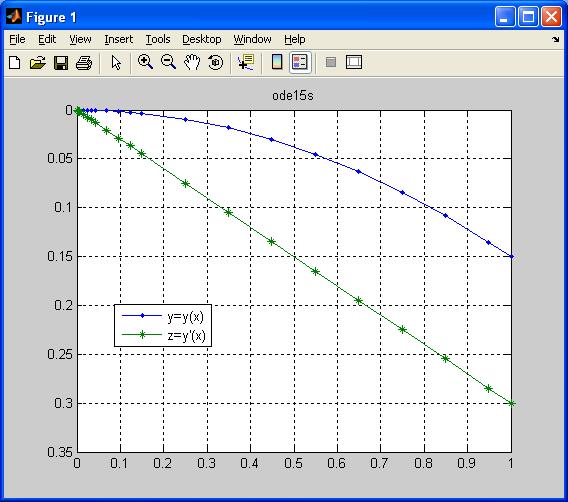
3. Использование встроенной функции ode15s, предназначенной для решения задачи Коши для систем обыкновенных дифференциальных уравнений 1-го порядка вида .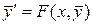
В данной функции реализуется многошаговый метод переменного порядка (от одного до пяти), использующий формулы численного дифференцирования «назад». Это адаптивный метод, рекомендуемый к применению в случае, когда ode45 не обеспечивает решения (система уравнений жесткая). При этом, входные и выходные параметры при обращении к ode15s полностью совпадают с соответствующими параметрами функции ode45 .
Пример соответствующей M-функции (ниже задано , ):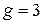
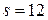function consol_ode15s
s=input('s=');
g=input('g=');
c=0.02*(s+g);
EJ=1/c;
x0xL=input('[x0 xL]=');
z0=input('[z10 z20]=');
[X Z]=ode15s(@F,x0xL,z0);
n=length(X);
fprintf('\n'),fprintf('%3s %6s %6s %6s','i','x','y','y'''),fprintf('\n')
for i=1:n
fprintf('%3d %6.4f %6.4f %6.4f\n',i,X(i),Z(i,:))
end
plot(X,Z(:,1),'.-',X,Z(:,2),'*-'),grid on
legend('y=y(x)','z=y''(x)',0),title('ode15s')
function dz=F(x,z)
dz=zeros(2,1);
dz(1)=z(2);
dz(2)=M(x)/EJ*sqrt((1+z(2)^2)^3);
end
function m=M(x)
m=1/sqrt((1+(c*x)^2)^3);
end
end
Результаты расчета:
s=12
g=3
[x0 xL]=[0 1]
[y0 z0]=[0 0]
i x y y'
1 0.0000 0.0000 0.0000
2 0.0021 0.0000 0.0006
3 0.0041 0.0000 0.0012
4 0.0062 0.0000 0.0019
5 0.0152 0.0000 0.0046
6 0.0242 0.0001 0.0073
7 0.0332 0.0002 0.0100
8 0.0422 0.0003 0.0127
9 0.0690 0.0007 0.0207
10 0.0957 0.0014 0.0287
11 0.1225 0.0023 0.0367
12 0.1492 0.0033 0.0448
13 0.2492 0.0093 0.0748
14 0.3492 0.0183 0.1048
15 0.4492 0.0303 0.1348
16 0.5492 0.0453 0.1648
17 0.6492 0.0632 0.1948
18 0.7492 0.0842 0.2248
19 0.8492 0.1082 0.2548
20 0.9492 0.1352 0.2848
21 1.0000 0.1500 0.3000
>>
