Базисный минор и ранг матрицы. Теорема о базисном миноре

Определение 1.5.1. Минором 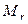порядка r матрицы 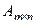( 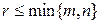) называется определитель порядка r, все элементы которого расположены на пересечении любых r строк и r столбцов этой матрицы.

Лемма 1.5.1.Если в матрице все миноры порядка r равны нулю, то равны нулю и все миноры более высоких порядков.

Доказательство.

Запишем определитель порядка r+1 и разложим его по элементам строки. После разложения, согласно теореме 1.3.1,определитель будет представлять собой сумму произведений элементов этой строки на их алгебраические дополнения, т. е. миноры порядка r с соответствующими знаками. По условию леммы такой определитель равен нулю.

Определение 1.5.2. В матрице А минор порядка r называется базисным, если он отличен от нуля, а все миноры порядка r+1, полученные присоединением к исходному одной строки и одного столбца, равны нулю или не существуют.

Миноры r+1 порядка из определения называются окаймляющими по отношению к исходному и содержат его целиком внутри себя. Столбцы и строки, на пересечении которых расположен базисный минор, будем называть базисными столбцами и строками.

Замечание 1.5.1.Базисный минор определяется неоднозначно, однако, все базисные миноры имеют одинаковый порядок.

Определение 1.5.3. Рангом матрицы называется порядок ее базисного минора. Обозначается: rang A.

Замечание 1.5.2.Из определения ранга матрицы следует

а) для произвольной матрицы 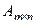выполняется: ;

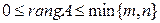b) 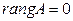тогда и только тогда, когда все элементы матрицы равны нулю, т.е. матрица А – нулевая;

c) дляквадратной матрицы А n-го порядка rangА = n тогда и только тогда, когда .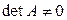

В общем случае для вычисления ранга матрицы будем использовать следующее правило: при вычислении ранга матрицы следует переходить от миноров меньших порядков к минорам больших порядков. Если уже найден минор r-го порядка 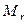, отличный от нуля, то требуется вычислить все миноры r+1 порядка, окаймляющие минор 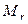. Если они все равны нулю или не существуют, то ранг матрицы равен r. Если хотя бы один из 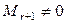, то с ним следует поступить также как с минором .

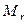Пример 1.5.1. Вычислить ранги следующих матриц:

a) 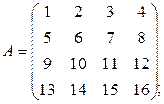b)

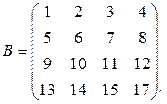
Решение:

a)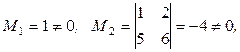

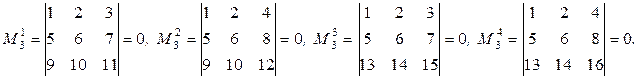
Базисным минором является минор 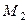,и тогда, согласно определению 1.5.3, rangA=2.

b)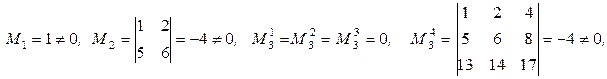

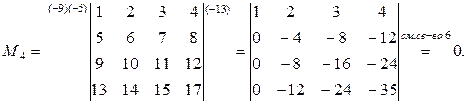
Базисным минором матрицы В является минор 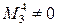. Следовательно, rang B =3.

Как мы видим из примеров, поиск ранга матрицы приводит к вычислению некоторого, быть может, очень большого, числа миноров этой матрицы. Существует еще один способ нахождения ранга матрицы, не связанный с вычислениями миноров. Этот метод основан на предварительном упрощении матрицы при помощи элементарных преобразований.

Определение 1.5.4. Элементарными преобразованиями над матрицей называются следующие преобразования строк (столбцов) матрицы: 1) перестановка двух строк (столбцов) местами; 2) умножение строки (столбца) на любое отличное от нуля число; 3) прибавление к одной строке (столбцу) другой строки (столбца), умноженной на произвольное число; 4) вычеркивание нулевой строки (столбца).

Определение 1.5.5. Матрицы А и В называются эквивалентными, если В можно получить из А с помощью конечного числа элементарных преобразований.

Эквивалентные матрицы будем обозначать следующим символом: А~В.

Теорема 1.5.1. Элементарные преобразования не изменяют ранга матрицы.

Действительно, если к матрице применить элементарные преобразования 1–3, то эти же преобразования или часть из них будут совершены и над ее базисным минором. Из свойств определителя 2, 9 и следствия к свойству 5 следует, что базисный минор, хотя численно и может поменяться, но в нуль в результате данных преобразований не обратится, т.е. ранг матрицы не изменится. Вычеркивание нулевой строки (столбца) так же не может изменить порядка базисного минора, т.е. ранг матрицы остается прежним.

Определение 1.5.6. Говорят, что прямоугольная матрица порядка 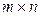имеет диагональную форму, если элементы 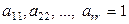( 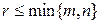), а все остальные элементы матрицы равны нулю.

Метод нахождения ранга матрицы при помощи элементарных преобразований состоит в следующем: для нахождения ранга матрицы нужно элементарными преобразованиями привести эту матрицу к диагональной форме и сосчитать количество единиц, стоящих в последней на главной диагонали.

Замечание 1.5.3. На практике для вычисления ранга матрицы удобно сочетать оба метода. А именно, приводя прямоугольную матрицу порядка 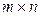к трапециевидной форме, вычислять миноры, используя пример 1.3.4.

Пример 1.5.2. Вычислить ранги матриц

а) 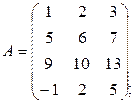b)

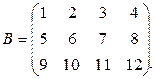
Решение:

а)

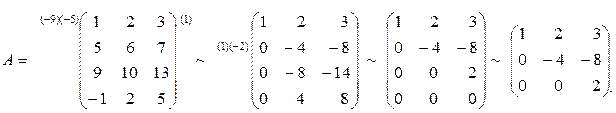
В результате элементарных преобразований над матрицей А получили эквивалентную ей верхнюю треугольную матрицу. Легко видеть, что

.

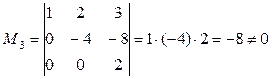Следовательно, rang A =3.

b)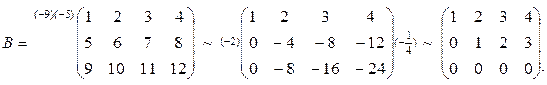

В матрице В минор 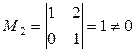, а миноров 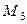нет. Следовательно, rangВ=2.

Пример 1.5.3. Найти ранг матрицы в зависимости от действительных значений параметра а:

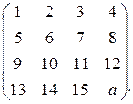
Решение.

Элементарными преобразованиями приведем матрицу к трапециевидной (или, если получится, к треугольной) форме:

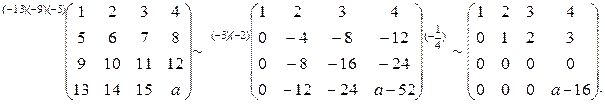
После вычеркивания нулевой строки получается прямоугольная матрица размера 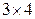, эквивалентная данной.

Если 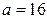, то имеем матрицу

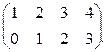
Ранг этой матрицы равен двум, так как она содержит, например, минор .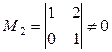

Если 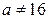, то имеем матрицу, ранг которой равен трем, так как она содержит минор .

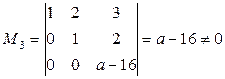Таким образом, 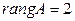, есл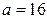и , и 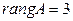, если .

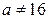Замечание 1.5.4. Матрица в примере 1.5.3 элементарными преобразованиями приведена к ступенчатому виду

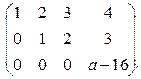
Ранг в этом случае можно также считать по количеству ненулевых строк. То есть, если 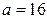, то имеем две ненулевых строки и 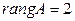; если 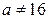, то имеем три ненулевых строки и .

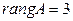Теорема 1.5.2 (о базисном миноре). Всякая строка (столбец) матрицы А есть линейная комбинация базисных строк (столбцов) этой матрицы.

Доказательство.

Пусть ранг матрицы А равен r. Можно считать, что базисный минор 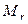расположен в левом верхнем углу матрицы. Если это не так, то заменой строк (столбцов) можно поместить этот минор в левый верхний угол. Окаймим матрицу базисного минора фрагментами i-й строки и j-го столбца матрицы A, где 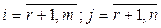. Рассмотрим определитель построенной матрицы

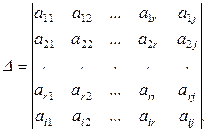
Определитель 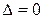как минор r+1 порядка в матрице с базисным миноромпорядка r. С другой стороны, раскладывая определитель по последнему столбцу (см. (1.3. 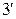)), получим:

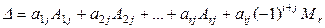. (1.5.1)

Здесь элемент 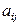стоит в (r+1)-й строке и (r+1)-м столбце определителя 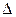, поэтому 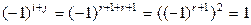. Так как 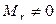, то разделив обе части равенства (1.5.1) на 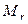, получим: 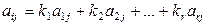, где 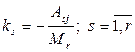. А это и означает, что i-я строка является линейной комбинацией первых r базисных строк.