Понятие определителя. Разложение определителя

по элементам строки (столбца)

Каждой квадратной матрице ставится в соответствие некоторое число, называемое определителем (детерминантом) матрицы. Для определителя матрицы А используют следующие обозначения: 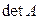, или ∆, или употребляют следующий символ: выписывают матрицу A, но вместо круглых скобок элементы матрицы заключают в прямые черточки.

Элементы, строки, столбцы, диагонали матрицы называют соответственно элементами, строками, столбцами и диагоналями определителя этой матрицы.

Для матрицы 1-го порядка определителем является значение единственного ее элемента, т. е. .

Рассмотрим понятие определителя для квадратных матриц 2-го и 3-го порядков.

Определение 1.3.1.Определителем 2-го порядка матрицы называется число, равное разности произведений элементов главной и побочной диагоналей, т.е.

. (1.3.1)

Определение 1.3.2.Определителем 3-го порядка матрицы называется число, вычисляемое по правилу:

. (1.3.2)

Существует ряд приёмов, облегчающих составление выражения, стоящего в правой части формулы (1.3.2). Рассмотрим некоторые из них:

1) правило треугольника.

Слагаемые в формуле (1.3.2) берутся со знаком “+”, если сомножители в соответствующих произведениях являются элементами главной диагонали определителя или вершинами треугольника, меньшая сторона которого параллельна главной диагонали; со знаком “–”, если сомножители являются элементами побочной диагонали определителя или вершинами треугольника, меньшая из сторон которого параллельна побочной диагонали. Для наглядности используется схема:

2) правило Саррюса*.

В следующей схеме используется матрица, полученная из матрицы приписыванием снизу первых двух ее строк. Произведения элементов, стоящих на главной диагонали, или на прямых параллельных главной диагонали, берутся со знаком “+”; а произведения элементов, стоящих на побочной диагонали или на прямых, параллельных ей, берутся со знаком “–”:

+

–

+

–

+ +

–

Замечание 1.3.1.Иногда для вычисления определителя 3-го порядка по правилу Саррюса используют матрицу, полученную из приписыванием справа первых двух столбцов.

Пример 1.3.1. Вычислить определители

a) b)

Приведенные выше схемы справедливы только для определителей 3-го порядка. Для вычисления определителей произвольного порядка будем использовать теорему, позволяющую свести вычисление определителя n-го порядка к вычислению определителей (n–1)-го порядка. С этой целью введем следующие понятия.

Определение 1.3.3.Минором элемента 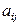определителя n-го порядка называется определитель (n–1)-го порядка, полученный из данного вычеркиванием i-й строки и j-го столбца, на пересечении которых находится этот элемент.

Определение 1.3.4.Алгебраическим дополнением 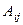элемента 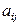называется его минор, взятый со знаком “+” или “–” в зависимости от четности или нечетности суммы (i+j), т.е. .

Пример 1.3.2. Минором элемента определителя 2-го порядка из примера 1.3.1.а является определитель 1-го порядка, полученный из данного вычеркиванием 1-й строки и 2-го столбца, т.е. ; алгебраическим дополнением элемента будет

Минором элемента определителя 3-го порядка из примера 1.3.1.b является определитель 2-го порядка, полученный из данного вычеркиванием 2-й строки и 2-го столбца: ; алгебраическим дополнение элемента будет .

Замечание 1.3.2.Если элемент определителя стоит на “четном месте”, т. е. сумма номеров его строки и столбца – четная, то минор этого элемента совпадает с алгебраическим дополнением. В противном случае, минор и алгебраическое дополнение данного элемента отличаются знаком.

Теорема 1.3.1.Сумма произведений элементов какой-либо строки (столбца) определителя на свои алгебраические дополнения равна величине определителя:

, (1.3.3)

. (1.3. )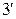

Cумма произведений элементов какой-либо строки (столбца) определителя на алгебраические дополнения соответствующих элементов другой его строки (столбца) равна нулю, т.е.

(1.3.4)

. (1.3. )

Формулы (1.3.3), (1.3.4) записаны для i-йстроки, а формулы(1.3. 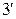), (1.3. ) для j-гостолбцаопределителя.

Равенства (1.3.3), (1.3. 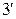) дают нам правило вычисления определителей n-го порядка и называются разложением определителя по i-й строке, j-му столбцу соответственно.

Пример 1.3.3. Определитель из примера 1.3.1.b можно вычислить разложением по первой строке:

Пример 1.3.4. Вычислить определитель верхней треугольной матрицы:

Раскладывая каждый раз данный определитель по элементам 1-го столбца, получаем, что он равен произведению своих диагональных элементов.

Используя разложение определителя по первой строке, можно получить такой же результат для нижней треугольной матрицы (1.1.3 ).

Замечание 1.3.3. При разложении определителя удобнее выбирать те строки (столбцы), которые содержат наибольшее число нулей.

Свойства определителей

1. При транспонировании матрицы ее определитель не меняется, т. е.

.

Покажем это на примере определителя 2-го порядка:

Следствие 1.4.1.Столбцы и строки в определителе равноправны, а именно: всякое утверждение для строк определителя будет верным и для столбцов.

2. Если в определителе поменять две строки (два столбца) местами, то определитель изменит свой знак на противоположный.

3. Если определитель содержит нулевую строку (столбец), то он равен нулю.

Это непосредственно следует из теоремы 1.3.1, если разложить определитель по нулевой строке.

4. Определитель, содержащий две одинаковых строки (столбца), равен нулю.

Доказательство.

Действительно, пусть 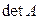имеет две одинаковые строки, т. е. соответствующие элементы i-й и k-й строк равны. Если эти строки поменять местами, то по свойству 2 определитель изменит свой знак на противоположный. На самом же деле, так как переставляются одинаковые строки, определитель не поменяется, т. е.

. Это равенство возможно, только в том случае, если .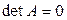

5. Если все элементы какой-либо строки (столбца) определителя имеют общий множитель, то его можно выносить за знак определителя.

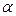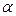Следствие 1.4.2.Если все элементы одной из строк (одного из столбцов) определителя увеличить в ( ) раз, то и сам определитель увеличится в раз.

6. Определитель, содержащий две пропорциональные строки (столбца), равен нулю.

Доказательство.

Пусть, например, элементы i-й строки определителя отличаются от соответствующих элементов k-й одним и тем же множителем 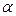. Вынося общий множитель 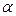из i-й строки за знак определителя, мы получаем две одинаковых строки. По свойству 4 такой определитель равен нулю.

7. Если все элементы i-й строки (j-го столбца) определителя n-го порядка представлены в виде суммы двух слагаемых: , то определитель равен сумме двух определителей, у которых все строки, кроме i-й (все столбцы, кроме j-го), – такие же, как и в данном определителе, а i-я строка (j-й столбец) в первом состоит из элементов , а во втором – из элементов 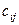, т.е.

Это свойство называют правилом сложения определителей.

Определение 1.4.1. Говорят, что строка определителя является линейной комбинацией других его строк, если каждый элемент этой строки равен сумме соответствующих элементов других строк, умноженных на некоторые числа.

Аналогичное определение можно сформулировать и для столбцов определителя.

8. Если одна из строк (столбцов) определителя есть линейная комбинация других его строк (столбцов), то определитель равен нулю.

Доказательство.

Пусть, например, i-я строка определителя представляет собой линейную комбинацию k-й и l-й строк, т. е. . На основании свойства 7 такой определитель равен сумме двух определителей, у которых все строки, кроме i-й такие же, как и в исходном, а i-я строка в первом из них будет состоять из элементов вида ,а во втором – из элементов . В получившихся определителях содержатся пропорциональные строки, следовательно, по свойству 6, они равны нулю. Таким образом, мы доказали равенство нулю исходного определителя.

9. Величина определителя не изменится, если к какой-либо строке (столбцу) прибавить другую строку (столбец), умноженную на произвольное число.

Доказательство.

Предположим, что к i-й строке прибавили k-ю, умноженную на некоторое число 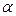. Тогда элементы i-й строки нового определителя имеют вид: .На основании свойства 7, этот определитель равен сумме двух определителей: первый совпадает с исходным, а второй равен нулю, так как содержит две пропорциональные строки.

Замечание 1.4.1. На практике для вычисления определителей удобно применять их свойства. Особенно полезным оказывается использование свойства 9 вместе с теоремой1.3.1 о разложении определителя по элементам строки (столбца). А именно, свойство 9 позволяет преобразовать определитель так, чтобы в любой строке или любом столбце все элементы, кроме одного, заменились нулями. Затем, раскладывая определитель по этой строке (столбцу), мы сводим вычисление определителя n-го порядка к вычислению определителя (n–1)-го порядка.

Пример 1.4.1. Вычислить определитель: