Операции над матрицами и их свойства

I. Сложение матриц

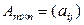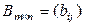Определение 1.2.1.Суммой двух матриц и называется матрица 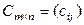такая, что

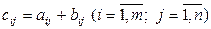, (1.2.1)

т.е. каждый элемент матрицы С равен сумме соответствующих элементов матриц А и В.

Сумма матриц А и В обозначается A+B.

Пример 1.2.1.

Дано

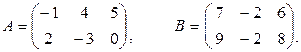
Найти А+В.

Решение.

A+B=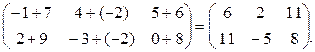

II. Умножение матрицы на число

Определение 1.2.2.Произведением матрицы 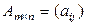на число 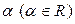называется матрица 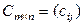такая, что

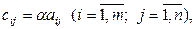(1.2.2)

т.е. каждый элемент матрицы С равен произведению соответствующего элемента матрицы А на число .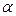

Для произведения матрицы на число используют обозначение .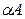

Пример 1.2.2.

Дано

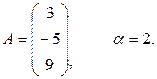
Найти .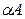

Решение.

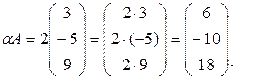
Определение 1.2.3.Матрицу –A=(–1)A будем называть противоположной по отношению к матрице A.

Следствие 1.2.1. Разность матриц А и В определяется как сумма матриц А и (–В):

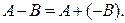
Пример 1.2.3. Найти разность А–В для матриц из примера 1.2.1.

Решение.

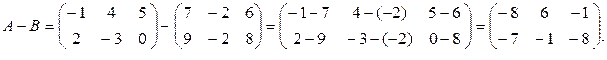
Свойства операций сложения и умножения на число:

1. 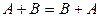(коммутативность сложения).

2. 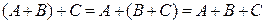(ассоциативность сложения).

3. .

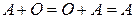4. .

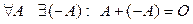5. ,

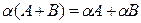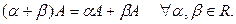
6. .

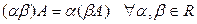7. .

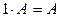Данные свойства представляются очевидными, так как сложение матриц и умножение их на число сводится к сложению и, соответственно, умножению чисел, а для чисел свойства 1–7 справедливы.

III. Произведение матриц

Операция умножения вводится только для тех пар матриц, у которых число столбцов первой матрицы совпадает с количеством строк второй.

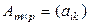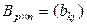Определение 1.2.4.Произведением матриц и называется матрица 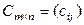такая, что

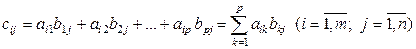, (1.2.3)

т.е. каждый элемент 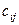матрицы С, расположенный в i-й строке и j-м столбце, равен сумме произведений элементов i-й строки матрицы A на соответствующие элементы j-го столбца матрицы B.

Произведение матриц А и В обозначается A·B.

Замечание 1.2.1.Матрица-произведение состоит из стольких строк, сколько их в первом сомножителе, и из стольких столбцов, сколько их во втором.

Пример 1.2.4.

Дано

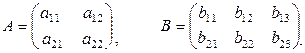
Найти A·B.

Решение.

Для пары матриц A, B операция умножения определена, так как число столбцов матрицы А совпадает с количеством строк матрицы B, причем 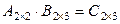. Используя формулу (1.2.3), найдем:

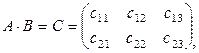
где

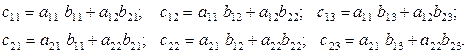
Пример 1.2.5.

Дано

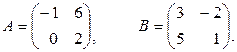
Найти A·B и B·A.

Решение.

Матрицы А и В – квадратные 2-го порядка, следовательно, произведения A·B и B·A определены и будут являться также квадратными матрицами 2-го порядка:

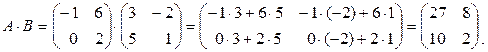
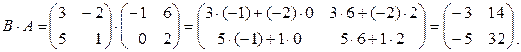
Замечание 1.2.2.Произведение матриц B·A из примера 1.2.4 не определено, так как количество столбцов матрицы B не равно количеству строк матрицы А.

Определение 1.2.5.Целой положительной степенью 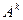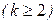квадратной матрицы А называется произведение k-матриц, каждая из которых равна A.

Очевидно, что порядок матриц 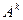и А одинаковый.

Пример 1.2.6.

Дано

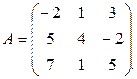
Найти .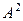

Решение.

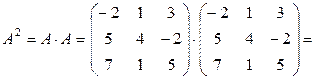
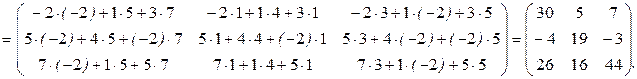
Свойства операции умножения матриц:

1. 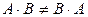(некоммутативность умножения).

2. 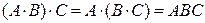(ассоциативность умножения).

3. 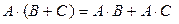(левосторонняя дистрибутивность умножения

относительно сложения).

4. 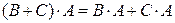(правосторонняя дистрибутивность умножения относительно сложения).

Свойства 1– 4 выполняются для произвольных матриц А, В и С, однако, предполагается, что матрицы имеют размеры, обеспечивающие возможность их перемножения и сложения.

Замечание 1.2.3.В ряде случаев может выполняться 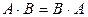, тогда матрицы A и B называются перестановочными или коммутирующими.

Замечание 1.2.4. Единичная матрица является перестановочной с любой квадратной матрицей того же порядка, т. е.

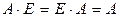. (1.2.4)

Некоммутативность произведения непосредственно следует из формулы (1.2.3), примеров 1.2.4, 1.2.5 и замечания 1.2.2.

Докажем свойство 2.

Дано

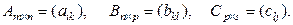
Доказать (A·B)·C=A∙(B·C).

Доказательство.

Введем обозначения:

.

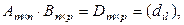
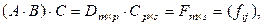
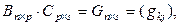
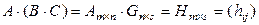Как мы видим, соответствующие произведения матриц слева и справа определены и результат произведений – матрицы F и H имеют одинаковый размер. Покажем, что соответствующие элементы этих матриц равны.

Используя формулу (1.2.3), получим:

,

.

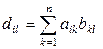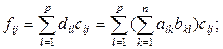
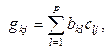
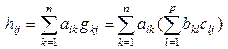Элементы 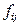и 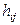отличаются лишь порядком суммирования. Однако, так как суммирования по индексам k и l происходят независимо друг от друга, то порядок их выполнения безразличен. Таким образом, из определения 1.1.2 следует, что F=H.

Свойства 3 и 4 доказываются аналогично свойству 2.

IV. Транспонирование матриц

Пусть дана матрица .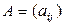

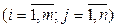Определение 1.2.6.Матрица 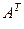, полученная из матрицы А заменой каждой ее строки столбцом с тем же номером, называется транспонированной по отношению к А.

Таким образом, если

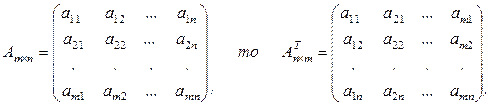(1.2.5)

т.е. .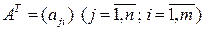

Переход от матрицы А к 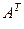называется транспонированием.

Пример 1.2.7.

Дано

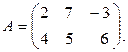
Найти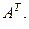

Решение.

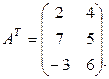
Свойства операции транспонирования:

1. .

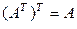2. .

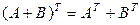3.

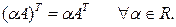
4.

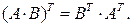
Замечание 1.2.5.Свойства линейности 2 и 3 можно заменить более общим:

.

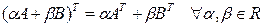Определение 1.2.7.Квадратная матрица 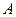называется симметричной, если 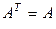и кососимметричной, если .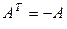