Тема : Численное решение уравнений в частных производных

Рассмотрим смешанную задачу для уравнения теплопроводности, а именно, найти функцию , удовлетворяющую уравнению

(7.1)

начальному условию

, (7.2)

и краевым условиям

, . (7.3)

Задачу будем решать методом сеток (конечных разностей). В основе метода лежит идея замены производных конечно-разностными отношениями. Ограничимся случаем двух независимых переменных. Пусть в плоскости хОу имеется некоторая область с границей (рис. 1).

Рис 1

Построим на плоскости два семейства параллельных прямых:

, , i=0,1,2,…, k=0,1,2,…

Точки пересечения этих прямых назовем узлами. Два узла называются соседними, если они удалены друг от друга в направлении оси Ох или Оу на расстояние, равное шагу сетки h или l соответственно. Выделим узлы, принадлежащие области G+Г, а также некоторые узлы, не принадлежащие этой области, но расположенные на расстоянии, меньшем чем шаг, от границы Г. Те узлы, у которых все четыре соседних узла принадлежат выделенному множеству узлов, называются внутренними (узел А, рис. 1). Оставшиеся из выделенных узлов называются граничными (узлы В, С). Обозначим

Значения искомой функции и=и(х,у) в узлах сетки будем обозначать через В каждом внутреннем узле заменим частные производные разностными отношениями:

В граничных точках воспользуемся формулами вида

, .

Аналогично заменяются частные производные второго порядка

Сделаем переход от уравнения вида к разностному уравнению

- =0.

После замены и преобразований получаем уравнение для вычисления внутренних узлов

(7.4)

При разностное уравнение (7.4) устойчиво [7]. Наиболее простой вид уравнение имеет при В этом случае уравнение (7.2) запишется в виде

(7.5)

Пусть (x,t) – точное решение задачи (7.1)-(7.3), – отклонение точного значения от вычисленного по методу сеток. Тогда погрешность вычислений может быть вычислена по формуле

, (7.6)

где = , где

Задание 1

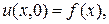
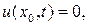
Используя метод сеток, найти приближенное решение уравнения (7.1)-(7.3), удовлетворяющее условиям 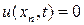, для 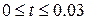, 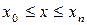и h=0.1, l=0.005.

Решение должно быть оформлено в виде таблицы 7.1 подсчитанной вручную. Исходные данные заданы в таблице 7.2. Оценить погрешность вычислений по формуле (7.6).

Комментарий. Значения 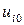находим, подставляя значение х_о в 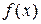. Например, 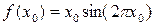при 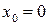равна 0. Значения 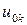и 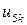определяются краевыми условиями (в нашем случае нулевые). Далее значение, например, 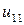находим, используя формулу (7.5), т.е. 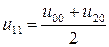и т.д.

Таблица 7.1.

j
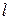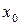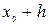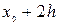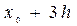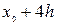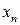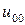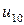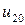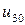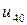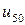	0.005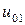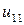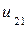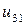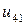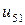
	0.010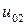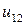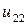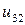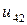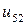
	0.015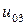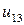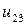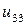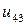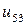
	0.020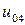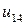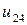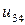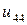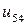
	0.025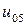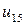
	0.03

Таблица 7.2

№ варианта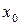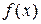
	0.1	0.6
		0.5
	0.2	0.7
		0.5
	0.1	0.6
	0.2	0.7
		0.5
	0.2	0.7
		0.5
	0.1	0.6

Примерный фрагмент выполнения лабораторной работы

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. В чем суть метода сеток?

2. Какие точки называются узлами?

3. Что такое шаг сетки?

4. Какие узлы называются внутренними и какие граничными?

5. Как перейти от дифференциального уравнения к разностному (на примере уравнения теплопроводности)?

6. Какое уравнение используется для вычисление текущего слоя?

7. Как вычислить отклонение значений точного решения от приближенного по методу сеток?

Литература

1. Заварыкин В.М., Житомирский В.Г., Лапчик М.П. Численные методы. М.: Просвещение. – 1991. – 175с.

2. Ракитин В.И., Первушин В.Е. Практическое руководство по методам вычислений. М.: Высшая школа. – 1998. 384с.

3. Волков Е.А. Численные методы. М.: Наука. – 1987. – 248 с.

3. Турчак Л.И. Основы численных методов. М.: Наука. – 1987. – 318с.

4. Копченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах. М.: Наука. – 1972. – 366с.

5. Березин И.С., Жидков Н.П. Методы вычислений. Т.1. М.: Наука. – 1966. – 632с.

6. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. М. – С.П.: Физматлит. – 2001. – 630с.

7. С. Ф. Аминова, Р. М. Асадуллин. Лабораторный практикум по курсу «Численные методы».- Уфа: Изд-во БГПУ, 2003 –28с.

8. Р. Р. Сулейманов. Решение математических задач в системе MathCAD 8.1 // Учитель Башкортостана. 2002. № 2.

10. MATHCAD 6.0 PLUS/ Финансовые, инженерные и научные расчеты в среде Windows 95./ Пер. с англ. – М.: Информационно-издательский дом "Филинъ", 1996. – 712 с.

11. Плис А.И., Сливина Н.А. Mathcad: математический практикум. – М.: Финансы и Статистика. – 1999.

12. Очков В.Ф. Mathcad 8 Pro для студентов и инженеров. – М.: КомпьютерПресс, 1999.

13. Очков В.Ф.. MathCad 7 Pro для студентов и инженеров. – М.: КомпьютерПресс, 1998. – 384 с.

14. Дьяконов В.П. Справочник по MathCAD PLUS 6.0 PRO. – М.: CK Пресс, 1997. – 336 с.

Содержание.

Введение.

Знакомство с MathCad

Вычисления и операции в MathCad

Лабораторная работа №1

Решение уравнений с одной переменной

Лабораторная работа №2

Решение систем линейных уравнений

Лабораторная работа №3

Численное интерполирование

Лабораторная работа №4

Численное интегрирование

Лабораторная работа №5

Численное решение дифференциальных уравнений

Лабораторная работа №6

Статистическая обработка данных.

Лабораторная работа №1

Численное решение уравнений в частных производных

Литература.